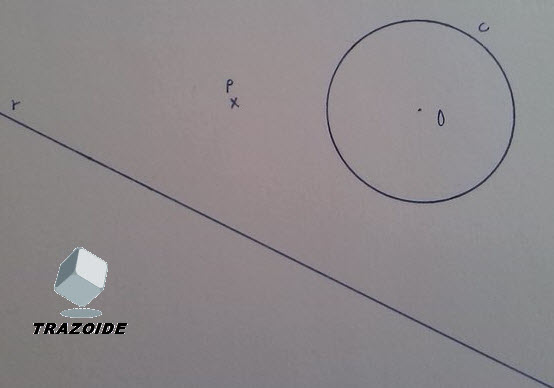
Dadas la recta r, la circunferencia c y el punto P se pide:
-1) Dibujar la circunferencia ortogonal a r y a c que pasa por P
También se propone una variante del ejercicio:
-2) Dibujar la circunferencia de radio más pequeño ortogonal a c y tangente a r que pasa por P.
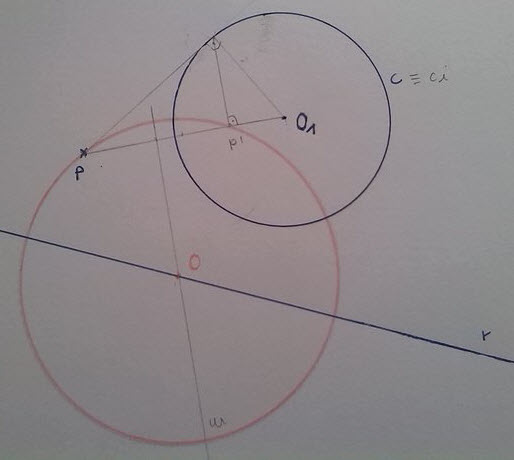
1) Sé que para que la circunferencia solución sea ortogonal a r, su centro deberá estar en esta, por tanto r es el l.g. de los centros solución
Si el centro de la circunferencia está en r y esta pasa por P, también pasará por el simétrico de P con respecto a la circunferencia.
Se me ha ocurrido intentarlo por potencia, puesto que P y su simétrico me dan un eje radical del haz de circunferencias que pasan por ellos y
tienen centro en r.
Además, haciendo una circunferencia auxiliar con centro en r que pase por P obtendría de su intersección con la circunferencia
dada otro eje radical. La intersección de ambos ejes radicales me daría el centro radical. A partir de aquí no sé como seguir.
2) He intentado abordar el ejercicio por inversión, tomando la circunferencia dada como circunferencia de puntos dobles, así la circunferencia solución, que será ortogonal a la dada, será inversa de sí misma. También he hallado el inverso del punto P y he hecho la mediatriz del segmento que los une, en la cual estará el centro (pues la circunferencia que pasa por un punto y su inverso es inversa de sí misma, y por tanto ortogonal a la circ. de puntos dobles). Aquí me he quedado
Adjunto una foto del enunciado. Espero que me haya expresado bien.
Un saludo y gracias.

 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado