Hola, buenas tardes.
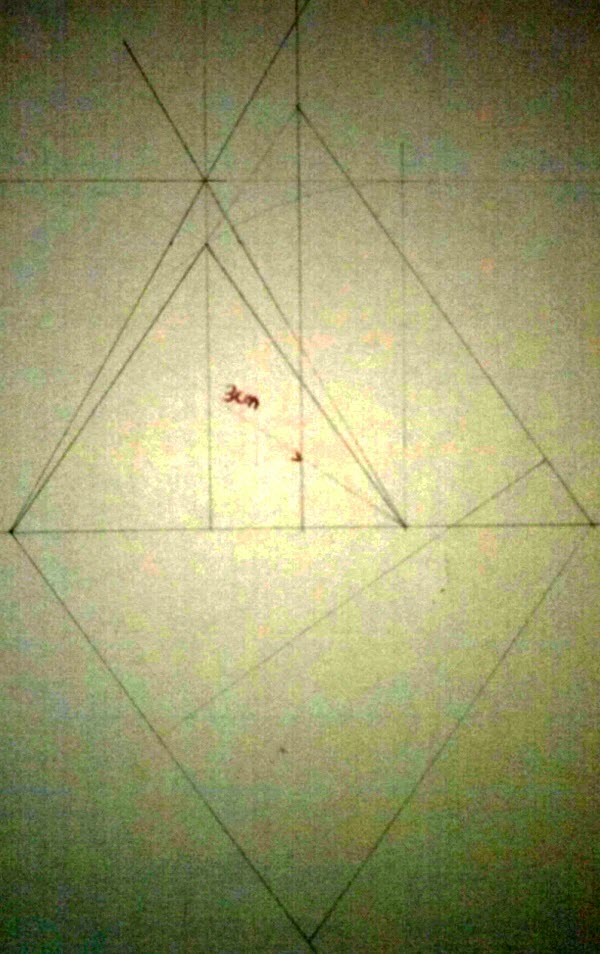
La razón por la que escribo es porque estoy intentando resolver un problema en el que necesito conocer la magnitud de la diagonal de un octaedro del que sólo conozco que la distancia entre caras opuestas es 6 cm. Para hallar la magnitud de la diagonal sé que tengo que hacer la sección principal pero el problema es que con el dato de partida que me dan no sé hacerla. Agradecería mucho si alguien me pudiera ayudar a resolverlo.
Muchas Gracias, un saludo.
Sección principal de un octaedro
Reglas del Foro
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
-
giraldillo1993
- USUARIO

- Mensajes: 3
- Registrado: Sab, 17 Nov 2012, 17:54
Sección principal de un octaedro
Esta es la típica cuestión en los poliedros en la que necesitas conocer una dimensión, y te dan otra dimensión menos frecuente, como la distancia entre caras, radio de la esfera circunscrita, etc...
Todos se inician dibujando la correspondiente sección principal con un tamaño arbitrario y luego estableciendo una proporcionalidad mediante Thales obtienes la dimensión que quieras a partir de la que te dan. Ten en cuenta que las relaciones métricas que hay en una sección principal son constantes; o sea, mantienen una proporcionalidad.
Por tanto, si sabes construir la sección principal de un octaedro, y sabes aplicar Thales, no debes tener ningún problema en hallar la dimensión que quieras a partir de la distancia entre caras opuestas.
Todos se inician dibujando la correspondiente sección principal con un tamaño arbitrario y luego estableciendo una proporcionalidad mediante Thales obtienes la dimensión que quieras a partir de la que te dan. Ten en cuenta que las relaciones métricas que hay en una sección principal son constantes; o sea, mantienen una proporcionalidad.
Por tanto, si sabes construir la sección principal de un octaedro, y sabes aplicar Thales, no debes tener ningún problema en hallar la dimensión que quieras a partir de la distancia entre caras opuestas.
-
giraldillo1993
- USUARIO

- Mensajes: 3
- Registrado: Sab, 17 Nov 2012, 17:54
He estado intentándolo varias veces pero me encuentro que una vez que elijo un triangulo equilátero de partida, hallo su sección principal y aplico proporcionalidad, la sección principal que busco depende del tamaño del triangulo equilátero del que partí... y esto no puede estar bien así que me estaré equivocando en la construcción.
-
giraldillo1993
- USUARIO

- Mensajes: 3
- Registrado: Sab, 17 Nov 2012, 17:54
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
He modificado tu imagen para aclararla porque estaba muy oscura y no se veía nada. La próxima vez ilumina con alguna lámpara o cerca de una ventana.
Como en todo dibujo que está acabado, no veo claro cuál es el inicio y el final, es decir, cuales son los pasos que has seguido. Tampoco das una descripción escrita de los pasos que has seguido. Así que te comento como hacerlo.
Determinación de la diagonal de un octaedro, D, conocida su distancia entre dos caras opuestas, H (altura del octaedro).
Vamos a dibujar media sección principal a partir de una medida de la arista cualquiera.
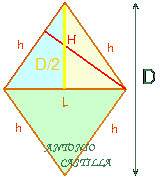
1 - Con una medida cualquiera L' dibujar un triángulo equilátero.
2 - Trazar la altura, h', de ese triángulo equilátero.
3 - Con las medidas de la arista L' y su altura de cara h', dibujar un triángulo isósceles en el que L' es el lado desigual y h' los dos lados iguales.
4 - Desde el vértice donde se unen dos lados distintos, L' y h', hacer una perpendicular al lado opuesto. Esto nos da H', altura de cuerpo (o principal) del octaedro de arista L' (no del que buscamos).
5 - Si desde el vértice común a los dos lados iguales, h', se traza una perpendicular al L' se tiene la mitad de la diagonal de cuerpo (o principal). D'/2, del octaedro de lado L'.
6 - Ahora se trata de ampliar o reducir (homotecia, semejanza o teorema de Thales, llámalo como quieras). Colocar sobre H' la distancia entre caras (altura principal) que nos han dado, H.
7 - Por su extremo hacer una paralela al lado del triángulo, h', y prolongar los otros dos. Hemos construido un triángulo homotético (o semejante). Si desde el vértice donde se cortan los dos lados iguales trazas una perpendicular al lado desigual obtienes la mitad de la diagonal, D/2, del octaedro buscado.
He modificado tu imagen para aclararla porque estaba muy oscura y no se veía nada. La próxima vez ilumina con alguna lámpara o cerca de una ventana.
Como en todo dibujo que está acabado, no veo claro cuál es el inicio y el final, es decir, cuales son los pasos que has seguido. Tampoco das una descripción escrita de los pasos que has seguido. Así que te comento como hacerlo.
Determinación de la diagonal de un octaedro, D, conocida su distancia entre dos caras opuestas, H (altura del octaedro).
Vamos a dibujar media sección principal a partir de una medida de la arista cualquiera.

1 - Con una medida cualquiera L' dibujar un triángulo equilátero.
2 - Trazar la altura, h', de ese triángulo equilátero.
3 - Con las medidas de la arista L' y su altura de cara h', dibujar un triángulo isósceles en el que L' es el lado desigual y h' los dos lados iguales.
4 - Desde el vértice donde se unen dos lados distintos, L' y h', hacer una perpendicular al lado opuesto. Esto nos da H', altura de cuerpo (o principal) del octaedro de arista L' (no del que buscamos).
5 - Si desde el vértice común a los dos lados iguales, h', se traza una perpendicular al L' se tiene la mitad de la diagonal de cuerpo (o principal). D'/2, del octaedro de lado L'.
6 - Ahora se trata de ampliar o reducir (homotecia, semejanza o teorema de Thales, llámalo como quieras). Colocar sobre H' la distancia entre caras (altura principal) que nos han dado, H.
7 - Por su extremo hacer una paralela al lado del triángulo, h', y prolongar los otros dos. Hemos construido un triángulo homotético (o semejante). Si desde el vértice donde se cortan los dos lados iguales trazas una perpendicular al lado desigual obtienes la mitad de la diagonal, D/2, del octaedro buscado.
¿Quién está conectado?
Usuarios navegando por este Foro: No hay usuarios registrados visitando el Foro y 20 invitados