.
Dada una circunferencia de centro A, su eje radical, E.R, hallar otra circunferencia cuya potencia respecto de un punto conocido P sea 30² y comparta el mismo eje radical.
1 - Dibujar un triángulo rectángulo en el que un cateto sea igual al radio de la circunferencia dada, AX, y el otro cateto igual al valor de la potencia, 30, sin estar elevada al cuadrado.
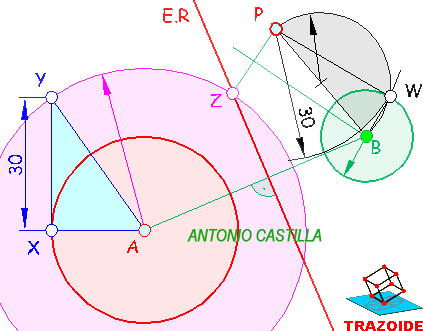
2 - Con centro en A y radio la hipotenusa del triángulo anterior se dibuja una circunferencia
3 - Esta circunferencia cortará al eje radical, E.R, en un punto Z.
4 - Unir Z con el punto dado P y hallar su mediatriz.
5 - Donde la mediatriz corte a la perpendicular al eje radical que pasa por A es el centro de la circunferencia buscada, B.
6 - Unir P con B, determinar su punto medio y dibujar una semicircunferencia con radio la mitad de PB.
7 - Con centro en P y radio la potencia, 30, sin elevarla al cuadrado, se traza un arco que cortará a la semicircunferencia, punto W.
8 - La distancia BW es el radio de la circunferencia buscada.
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí) El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado




