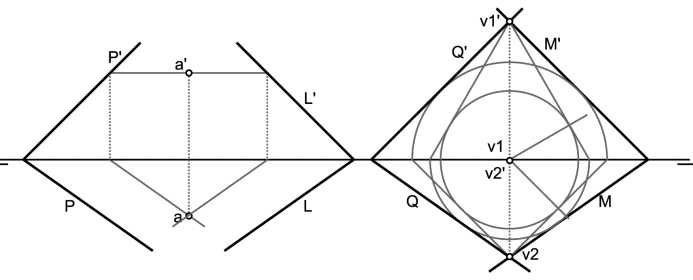
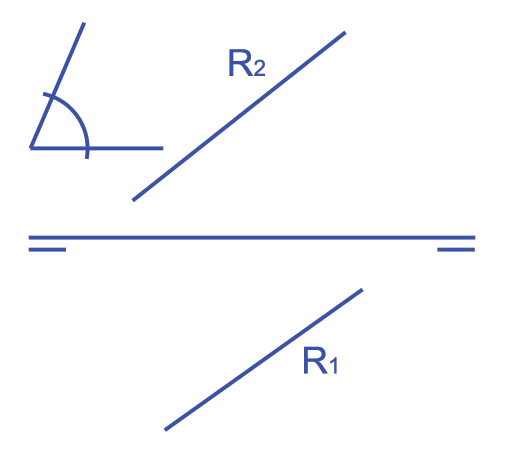
contener en R los planos (son dos) que forman el angulo dado con el PH de proyección
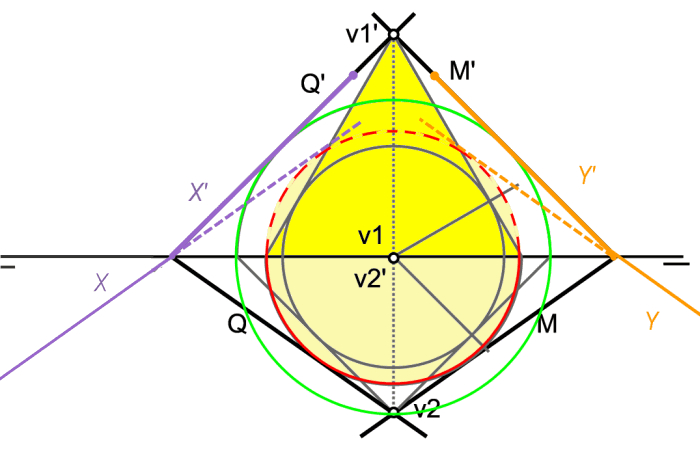
Lo he resuelto conteniendo en R un punto y trazando un cono con dicho punto como vertice, con la circunferencia directriz apoyada en PH y las generatrices formando el ángulo solicitado...luego tangentes a la circunferencia desde la traza horizontal hasta LT...luego de LT hasta la traza vertical de R y listo...
se dice rápido...y bueno, no es tanto...
pero sospecho que se debe poder hacer con cambios de plano...mas facil??
o con giros!?
Saludos
Gracias de antemano

 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado