5 círculos tangentes inscritos en triángulo equilátero
Reglas del Foro
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí) El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
-
Antonio Briones
- COLABORADOR

- Mensajes: 110
- Registrado: Vie, 29 Oct 2010, 18:27
5 círculos tangentes inscritos en triángulo equilátero
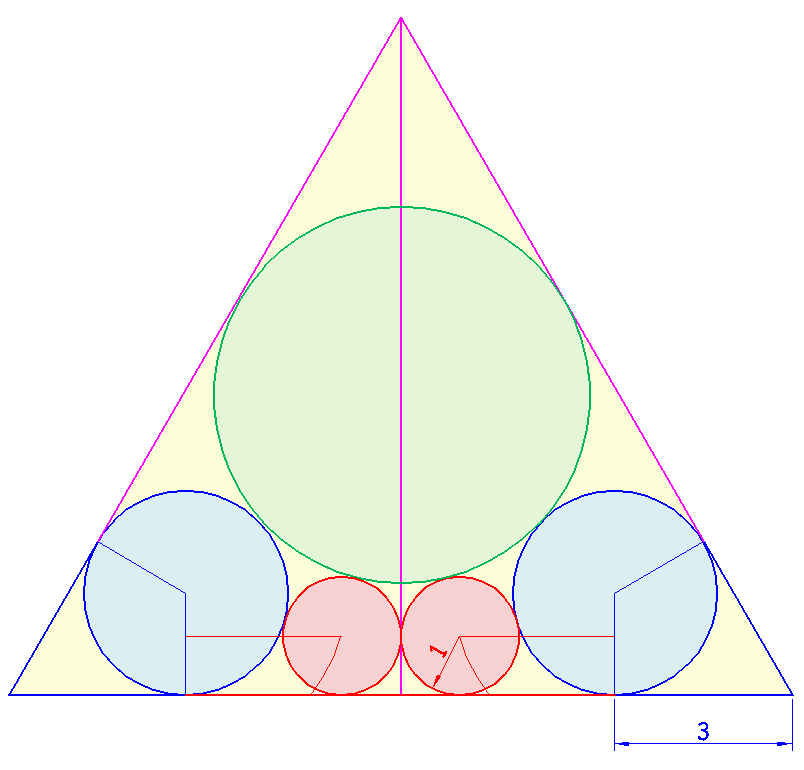
Dado un triángulo equilátero inscribir los círculos que se muestran, que yo he dibujado a ojo.
Quizá pueda resolverse por inversión. Los centros de los 4 círculos tangentes a la base
yacen en una parábola de foco el centro de la circunferencia mayor.
Gracias.
Quizá pueda resolverse por inversión. Los centros de los 4 círculos tangentes a la base
yacen en una parábola de foco el centro de la circunferencia mayor.
Gracias.
- Adjuntos
-
- triangulo-5-criunferencias-g.png (65.12 KiB) Visto 3370 veces
Re: 5 círculos tangentes inscritos en triángulo equilátero
Lo había intentado (analíticamente) varias veces, pero siempre terminaba riéndose de mí.
Hoy “me lo he cargado”, creo que dormiré tranquilo.
Olvido detalles de su construcción pues es trivial, su deducción creo que es “harina de otro costal”
Si alguien está interesado en la deducción analítica o particularidades, sin problema, preguntad.
Saludos
Hoy “me lo he cargado”, creo que dormiré tranquilo.
Olvido detalles de su construcción pues es trivial, su deducción creo que es “harina de otro costal”
Si alguien está interesado en la deducción analítica o particularidades, sin problema, preguntad.
Saludos
- Adjuntos
-
- triangulo-5-criunferencias-h.gif (4.76 KiB) Visto 3369 veces
Re: 5 círculos tangentes inscritos en triángulo equilátero
Todo mi gozo en un pozo??
En una de las comprobaciones que he hecho con AutoCAD noto un pequeño error.
Si alguien lo comprueba agradeceré me lo comunique.
Me temo que únicamente será una buena aproximación.
Gracias
En una de las comprobaciones que he hecho con AutoCAD noto un pequeño error.
Si alguien lo comprueba agradeceré me lo comunique.
Me temo que únicamente será una buena aproximación.
Gracias
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
Re: 5 círculos tangentes inscritos en triángulo equilátero
.
A mí me sale perfecto. Felicidades por la deducción.
¿Cuál es ese pequeño error del que hablas?
Ten en cuenta que cuando haces mucho zoom en AutoCad la imagen se desvirtua, se pixela y las curvas no se mantienen tangentes o pasando por donde deberían.
A mí me sale perfecto. Felicidades por la deducción.

¿Cuál es ese pequeño error del que hablas?
Ten en cuenta que cuando haces mucho zoom en AutoCad la imagen se desvirtua, se pixela y las curvas no se mantienen tangentes o pasando por donde deberían.
Re: 5 círculos tangentes inscritos en triángulo equilátero
Gráficamente tanto en AutoCAD como en GeoGebra al efectuar zoom, a mi me parece que falla una tangencia.
La deducción analítica la trabajo mediante un sistema de ecuaciones irracionales, tanto Derive como Wolfran alpha se rebelan en darme su solución. Manualmente creía haber encontrado la solución generalizada, pero compruebo que al sustituir en las ecuaciones por valores numéricos con Derive los decimales tampoco “cuadran”. Me temo que no es error de zoom o decimales, posiblemente únicamente solo sea una aproximación a la verdadera solución.
Creo que otra vez “con la iglesia hemos topado, amigo Sancho”
Gracias Antonio
La deducción analítica la trabajo mediante un sistema de ecuaciones irracionales, tanto Derive como Wolfran alpha se rebelan en darme su solución. Manualmente creía haber encontrado la solución generalizada, pero compruebo que al sustituir en las ecuaciones por valores numéricos con Derive los decimales tampoco “cuadran”. Me temo que no es error de zoom o decimales, posiblemente únicamente solo sea una aproximación a la verdadera solución.
Creo que otra vez “con la iglesia hemos topado, amigo Sancho”
Gracias Antonio
-
Marta García
- CONTRIBUIDOR

- Mensajes: 94
- Registrado: Vie, 07 Jul 2017, 11:11
Re: 5 círculos tangentes inscritos en triángulo equilátero
Hola, me ha parecido un ejercicio muy bonito y he intentado hacerlo. Vale. Las circunferencias pequeñas y el triángulo bien. Pero para situar la circunferencia central solo se me ocurre hallar la circunferencia tangente a dos rectas y a otra circunferencia. Primero he probado con la O sub 1 y no me da la tangencia a las circunferencias. Luego he probado con la de radio 1 y tampoco.Socorro! ¿ Qué estoy haciendo mal?
- Adjuntos
-
- triangulo-5-criunferencias-i.JPG (105.83 KiB) Visto 3368 veces
Re: 5 círculos tangentes inscritos en triángulo equilátero
Celebro que te hayas interesado por este problema. No he conseguido su solución, si bien por el camino me he topado con bastantes particularidades, dado tu interés te apunto una para que sigas con el dibujo.
La circunferencia central es una circunferencia tangente a los lados del triángulo y a una de las restantes circunferencias, o bien la circunferencia tangente a las cuatro inferiores o por simetría a tangente a dos y su centro sobre la altura de triángulo.
La particularidad que apunto es que la tangente común a las dos circunferencias inferiores corta a la altura en el punto de corte de esta con la circunferencia central (desconocida), el radio de la central será la distancia de este punto al vértice del triángulo. Esto sí creo que es exacto, los valores “1” y “3” del inicio de la construcción es una aproximación.
Saludos
La circunferencia central es una circunferencia tangente a los lados del triángulo y a una de las restantes circunferencias, o bien la circunferencia tangente a las cuatro inferiores o por simetría a tangente a dos y su centro sobre la altura de triángulo.
La particularidad que apunto es que la tangente común a las dos circunferencias inferiores corta a la altura en el punto de corte de esta con la circunferencia central (desconocida), el radio de la central será la distancia de este punto al vértice del triángulo. Esto sí creo que es exacto, los valores “1” y “3” del inicio de la construcción es una aproximación.
Saludos
-
Marta García
- CONTRIBUIDOR

- Mensajes: 94
- Registrado: Vie, 07 Jul 2017, 11:11
Re: 5 círculos tangentes inscritos en triángulo equilátero
Hola, me temo que esta última explicación no la he entendido. Probaré con algún otro método, ya que el de circunferencia tg a dos rectas y a otra circunferencia no me sale. Bueno gracias! Seguiré intentándolo
Re: 5 círculos tangentes inscritos en triángulo equilátero
yo estoy probando haciendo alguna analogia construyendo una construccion similar pero sin ser un triangulo equilatero y ver si hay algun punto en comun si hago 2 diferentes hasta conseguir el triangulo equilatero pero por ahora no hay suerte.
-
Marta García
- CONTRIBUIDOR

- Mensajes: 94
- Registrado: Vie, 07 Jul 2017, 11:11
Re: 5 círculos tangentes inscritos en triángulo equilátero
Bueno, al final sí que me ha salido por el método de circunferencia tangente a dos rectas y a otra circunferencia. Un saludo.
- Adjuntos
-
- triangulo-5-criunferencias-j.JPG (86.07 KiB) Visto 3367 veces
¿Quién está conectado?
Usuarios navegando por este Foro: No hay usuarios registrados visitando el Foro y 0 invitados



