Completando todo lo comentado por Antonio,creo q tu dificultad para imaginar el problema tridimensional viene porq parece q has obviado una cosa fundamental q es el metodo para pasar de una homografia tridimensional a una homologia plana.
Este paso se realiza,normalmente, o por proyeccion de los elementos de la homografia sobre un plano o bien otra forma es por abatimiento de esos elementos sobre el plano.
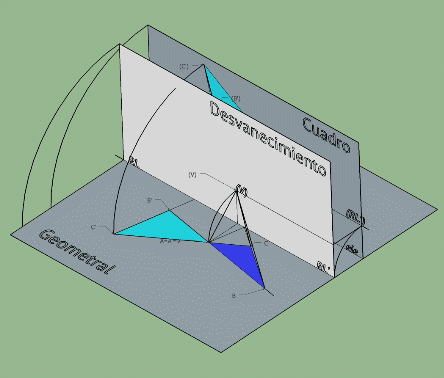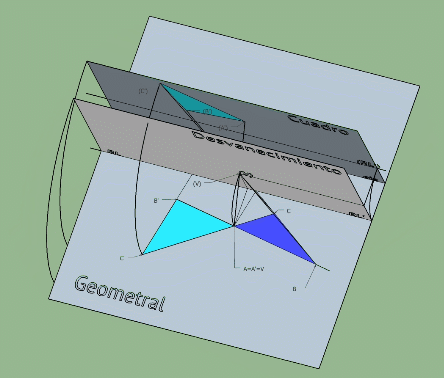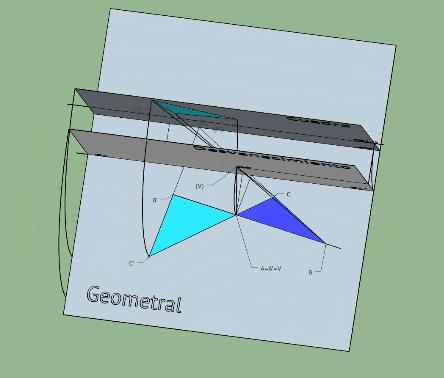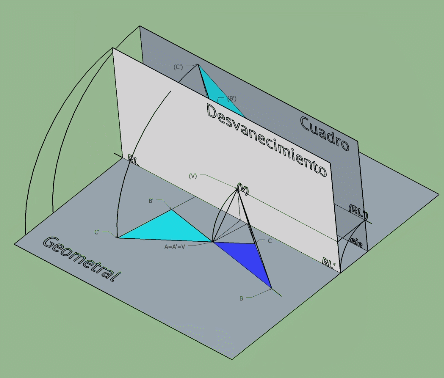
Te pongo un esquema q utilicé para otra consulta
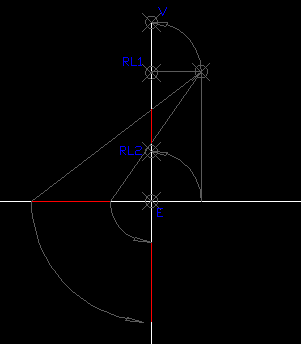
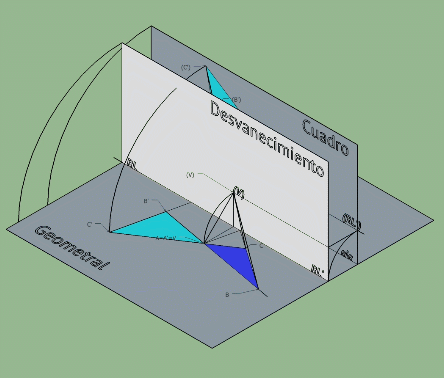
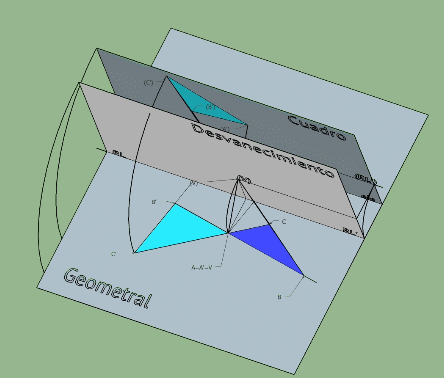
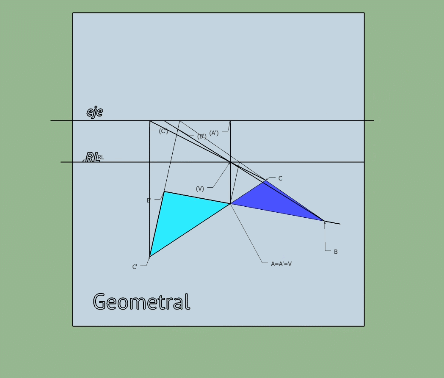
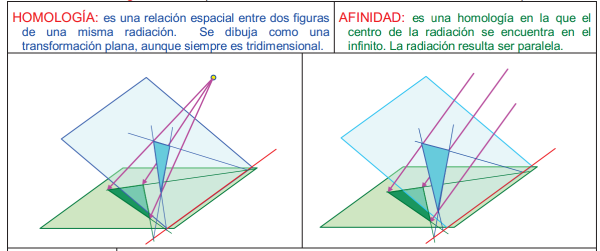
Esta imagen se corresponde con un abatimiento en sistema conico pero es esclarecedora de como pasar de una homografia tridimensional a una plana por abatimientos (el plano horizontal se abate sobre el plano vertical q será en este caso el plano de la homologia)
Observa como las rectas limites se generan trazando planos paralelos al horizontal y vertical desde el centro de la homografia.
El centro de la homologia plana generada en el plano vertical es el abatimiento del punto V empleando como charnela la recta limite RL1.
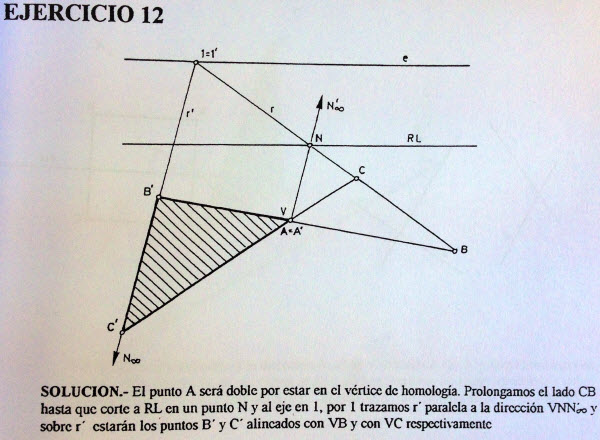
Pues ver q si las figuras homologas tienen un punto comun en el eje y q si el centro de la homografia lo situas en el cuarto cuadrante y sobre el bisector,obtendras una homologia plana en el q coincidiran 2 puntos homologos y el centro de homologia
Salu2

 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado