Circunferencia que comparte eje radical con otra
Reglas del Foro
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí) El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
Circunferencia que comparte eje radical con otra
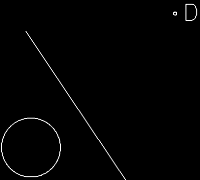
Conocida una circunferencia y el eje radical que comparte con otra circunferencia a obtener. Determinar esa circunferencia a obtener sabiendo que pasa por el punto D


- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
Dada una circunferencia, de centro A, y su eje radical, e, hallar una circunferencia que pasando por el punto P comparta ese mismo eje radical
1 - Trazar una circunferencia de centro cualquiera, x, que pase por el punto dado, P, y corte a la circunferencia dada.
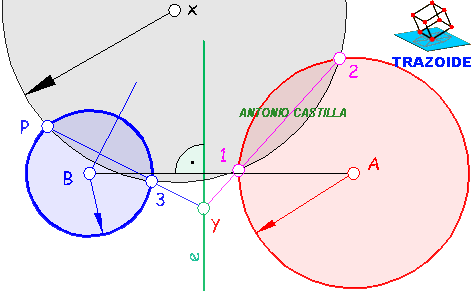
2 - Unir los puntos de corte,1 y 2, con la circunferencia inicial hasta que esta recta corte al eje radical, punto Y.
3 - Unir Y con el punto dado, P
4 - Trazar la mediatriz entre el punto dado, P, y donde la recta anterior corte a la auxiliar, 3.
5 - Donde la mediatriz corta a la recta perpendicular al eje radical que pasa por el centro de la circunferencia dada, A, es el centro de la circunferencia buscada, B.
Dada una circunferencia, de centro A, y su eje radical, e, hallar una circunferencia que pasando por el punto P comparta ese mismo eje radical
1 - Trazar una circunferencia de centro cualquiera, x, que pase por el punto dado, P, y corte a la circunferencia dada.

2 - Unir los puntos de corte,1 y 2, con la circunferencia inicial hasta que esta recta corte al eje radical, punto Y.
3 - Unir Y con el punto dado, P
4 - Trazar la mediatriz entre el punto dado, P, y donde la recta anterior corte a la auxiliar, 3.
5 - Donde la mediatriz corta a la recta perpendicular al eje radical que pasa por el centro de la circunferencia dada, A, es el centro de la circunferencia buscada, B.
-
YoliPocket
- USUARIO

- Mensajes: 0
- Registrado: Jue, 06 Feb 2014, 00:07
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
No sé si será corta pero esta es la explicación :
a - El eje radical dado, e, son todos los puntos que tiene la misma potencia respecto de la circunferencia dada y la buscada.

b - Dibujamos una circunferencia cualquiera que corte a la dada (para que sea rápido calcular su eje radical) y pase por el punto de la buscada (así sabemos que la está cortando o al menos es tangente).
c - Hallamos el eje radical entre la nueva circunferencia y la dada. Estos son todos los puntos que tienen la misma potencia entre las dos, pero donde ese eje radical corte al eje radical dado, punto Y, este será un punto (centro radical) que tendrá la misma potencia respecto de las tres circunferencias (la dada, la buscada y la nueva).
d - Si el centro radical, Y, lo hubiésemos calculado con la circunferencia buscada y la nueva también lo haríamos determinando su eje radical y comprobando donde corta al eje radical dado. Luego el eje radical entre la circunferencia buscada y la nueva pasará por el centro radical y por el punto de corte de las dos circunferencias, este punto es P. En definitiva, uniendo Y con P tenemos el eje radical entre la buscada y la nueva.
e - Si tuviésemos la circunferencia buscada el eje radical con la nueva se haría uniendo los puntos de corte de ambos. Aunque no tenemos la buscada sí tenemos el eje radical P-Y y el punto de corte en la nueva, 3, luego el punto 3 es otro punto de la circunferencia buscada.
f - Tenemos dos puntos de la circunferencia buscada, 3 y P, el centro de una circunferencia está en la mediatriz de dicho segmento.
g - Los ejes radicales son perpendiculares a la unión de los centros. Como tenemos el centro de la dada y el eje radical dado, desde el centro trazamos una perpendicular al eje radical y ahí estará el centro.
No sé si será corta pero esta es la explicación :
a - El eje radical dado, e, son todos los puntos que tiene la misma potencia respecto de la circunferencia dada y la buscada.

b - Dibujamos una circunferencia cualquiera que corte a la dada (para que sea rápido calcular su eje radical) y pase por el punto de la buscada (así sabemos que la está cortando o al menos es tangente).
c - Hallamos el eje radical entre la nueva circunferencia y la dada. Estos son todos los puntos que tienen la misma potencia entre las dos, pero donde ese eje radical corte al eje radical dado, punto Y, este será un punto (centro radical) que tendrá la misma potencia respecto de las tres circunferencias (la dada, la buscada y la nueva).
d - Si el centro radical, Y, lo hubiésemos calculado con la circunferencia buscada y la nueva también lo haríamos determinando su eje radical y comprobando donde corta al eje radical dado. Luego el eje radical entre la circunferencia buscada y la nueva pasará por el centro radical y por el punto de corte de las dos circunferencias, este punto es P. En definitiva, uniendo Y con P tenemos el eje radical entre la buscada y la nueva.
e - Si tuviésemos la circunferencia buscada el eje radical con la nueva se haría uniendo los puntos de corte de ambos. Aunque no tenemos la buscada sí tenemos el eje radical P-Y y el punto de corte en la nueva, 3, luego el punto 3 es otro punto de la circunferencia buscada.
f - Tenemos dos puntos de la circunferencia buscada, 3 y P, el centro de una circunferencia está en la mediatriz de dicho segmento.
g - Los ejes radicales son perpendiculares a la unión de los centros. Como tenemos el centro de la dada y el eje radical dado, desde el centro trazamos una perpendicular al eje radical y ahí estará el centro.
¿Quién está conectado?
Usuarios navegando por este Foro: No hay usuarios registrados visitando el Foro y 34 invitados

