
Homología afín de un cuadrado con dos puntos homólogos y dos rectas homólogas
Reglas del Foro
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
Homología afín de un cuadrado con dos puntos homólogos y dos rectas homólogas
Tengo problemas con este ejercicio. No sé trazar siquiera el eje de afinidad.


- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
1 - Uniendo A y A' se obtiene la dirección de afinidad.
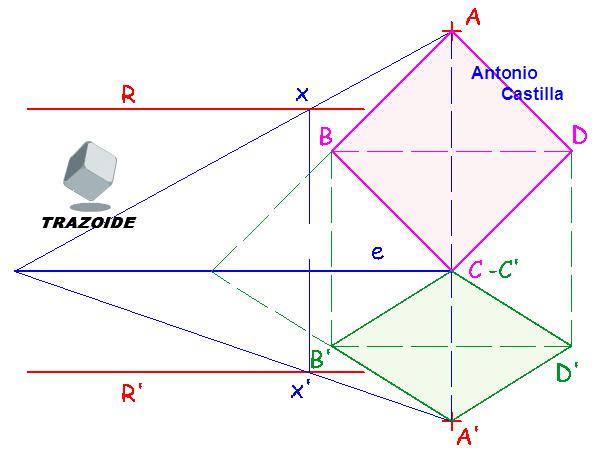
2 - Si una recta y su homóloga son paralelas también son paralelas al eje de afinidad. Por un punto, x, cualquiera de la recta R se dibuja una paralela a la dirección de afinidad, A-A', y se obtiene el afín x' sobre la recta homóloga R'.
3 - Unir A con x y A' con x'. El punto de corte de ambas es un punto del eje. Trazar por él una paralela a R o R' y tenemos el eje, e, de la afinidad.
4 - La longitud más corta entre A y un punto del eje es una perpendicular a él. Por lo tanto, si se dibuja una perpendicular al eje desde A se obtiene el vértice C.
5 - Por el punto medio de AC dibujar una perpendicular y llevar la mitad de AC hacia cada lado para conseguir los otros dos vértices B y D.
6 - Prolongar AB hasta cortar al eje, e, de la afinidad. Unir ese punto con A'. Por B dibujar una paralela a la dirección de afinidad, A-A', y donde corte a la anterior es B'.
7 - El homólogo de C es él mismo por estar en el eje.
8 - Para conseguir D se puede seguir el mismo procedimiento que para B', o en este caso como BC es paralelo al eje B'C' también lo será. Así que dibujamos por B' una paralela al eje y por D una paralela a la dirección de afinidad. Donde se corten es D'.
1 - Uniendo A y A' se obtiene la dirección de afinidad.

2 - Si una recta y su homóloga son paralelas también son paralelas al eje de afinidad. Por un punto, x, cualquiera de la recta R se dibuja una paralela a la dirección de afinidad, A-A', y se obtiene el afín x' sobre la recta homóloga R'.
3 - Unir A con x y A' con x'. El punto de corte de ambas es un punto del eje. Trazar por él una paralela a R o R' y tenemos el eje, e, de la afinidad.
4 - La longitud más corta entre A y un punto del eje es una perpendicular a él. Por lo tanto, si se dibuja una perpendicular al eje desde A se obtiene el vértice C.
5 - Por el punto medio de AC dibujar una perpendicular y llevar la mitad de AC hacia cada lado para conseguir los otros dos vértices B y D.
6 - Prolongar AB hasta cortar al eje, e, de la afinidad. Unir ese punto con A'. Por B dibujar una paralela a la dirección de afinidad, A-A', y donde corte a la anterior es B'.
7 - El homólogo de C es él mismo por estar en el eje.
8 - Para conseguir D se puede seguir el mismo procedimiento que para B', o en este caso como BC es paralelo al eje B'C' también lo será. Así que dibujamos por B' una paralela al eje y por D una paralela a la dirección de afinidad. Donde se corten es D'.
¿Quién está conectado?
Usuarios navegando por este Foro: No hay usuarios registrados visitando el Foro y 18 invitados

