Dibujo técnico, geometría y cad.
Términos relacionadas con cad.
CAD (DAO) – Cadista – DDD (Diseño orientado a cotas) – AEC – BIM – C.A.E – C.A.M – C.A.T – CSG – DEM – D.D.D – GIS – HVAC – HVACR – MCAD – MDE – MDT – TAO – CATIA – CIM – CMM – Diseño paramétrico – Estereolitografía – GD&T – IGES – Ingeniería inversa – Manufactura aditiva – Modelado 3D – Modelado por historia
Términos antiguos ya sustituidos por otros.
Pitipie – Oxitoma – Ortoma – Amblitoma – Cuadrado y un tercio (Diatesarón) – Cuadrado y medio (Diapente) – Doble cuadrado (Diapasón) – Sesquidécimo (Uno y un décimo) – Sesquiquinto (Uno y un quinto) – Sesquitercio (Sesquitercia, Uno y un tercio) – Triple – Diapasón-diapente – Sesquiáltera – Plombagina
Alfabeto griego.
Alfa (a, A) – Beta (b, B) – Gamma (g, G) – Delta (d, ¶, D) – Épsilon (e, E) – Dseta (Dseda, z, Z) – Eta (h, H) – Zeta (Zeda, Theta, q, J, Q) – Iota (i, I) – Kappa (k, |, K) – Lambda (l, L) – Mu (My, Mi, m, M) – Nu (Ny, Ni, n, N) – Xi (x, X) – Ómicron (o, O) – Rho (Ro, r, }, R) – Sigma (s, V, S) – Tau (t, t, T) – Ípsilon (u, U) – Phi (Fi, f, j, F) – Ji (c, C) – Psi (y, Y) – Omega (w, W)
Palabras acabadas en –triz.
Directriz – Generatriz – Separatriz – Limitatriz – Osculatriz – Tractriz – Bisectriz – Trisectriz – Mediatriz – Matriz – Indicatriz – Osculatriz
Palabras acabadas en –oide
Senoide – Cosenoide – Tangentoide – Concoide – Astroide – Cubocicloide – Centroide – Biesfenoide – Bigiroide – Cardioide – Catenoide – Epicicloide (Epitrocoide) – Hipocicloide (Hipotrocoide) – Pericicloide – Cicloide (Trocoide) – Cilindroide – Concoide (Conchoide) – Romboide – Conoide – Clotoide – Cuboide – Deltoide – Disfenoide – Ovoide – Elipsoide – Esferoide – Cardioide – Nefroide – Geoide – Giroide – Globoide – Helicoide – Helizoide – Hiperboloide – Metabigiroide – Metagiroide – Ovoide – Parabigiroide – Paraboloide – Paragiroide – Pelecoide – Planoide – Plegablesoide – Prismatoide – Prismoide – Toroide – Trapezoide – Trigiroide – Drepanoide
Tipos de planos eléctricos.
Esquema unifilar – Esquema unifilar simplificado – Esquema multifilar – Esquema topográfico eléctrico – Esquema funcional – Esquema en planta
Inicio > Geometría plana > Enlaces y tangencias
La figura muestra la forma de las PALETAS DE UN VENTILADOR formada por arcos de circunferencia tangentes entre sí, las medidas están en cm, se pide:
Reproducir el dibujo en cartulina canson en formato A3 a escala natural, todos los trazos auxiliares y de construcción no debe borrarse, no incluya cotas.
SOLUCIÓN
1 – Con centro en A y radios 1, 2 y 16 se dibujan tres circunferencias concéntricas.
2 – Se dibujan tres ejes separados 360º/3 = 120º, colocados como se ven en la imagen.
3 – Sobre el eje vertical (en los otros dos hay que hacer lo mismo pero me referiré a este) y desde A se lleva hacia abajo una medida igual a 2 + 2 y tenemos la posición del centro B.
4 – Con centro en B y radio 2 dibujar un arco.
5 – Con centro en B y radio 2 + 4 se traza un arco. Dibujar una paralela al eje vertical a una distancia de 4 – 2 hacia la derecha. Donde esta paralela se corte con el arco anterior es el centro C. Dibujar el arco de centro C y radio 4.
6 – Paralelo al eje vertical dibujar otro hacia la derecha separado 13.
7 – Para la circunferencia de centro D se debe plantear el problema de dibujar las circunferencias tangentes a dos circunferencias (la de centro C y la de centro A de radio 16) y a una recta (la separada 13).
Puedes ver varios casos resueltos en https://trazoide.com/enlaces_y_tangencias.html#desconociendo-RADIO bajo el título «Circunferencia, Circunferencia, Recta – CCR», por ejemplo en https://trazoide.com/foro/potencia/circunferencia-tangente-una-recta-dos-circunferencias-radio-diferentes-t6731.html#p19840
8 – Sobre el eje que sube hacia la derecha y desde el punto A medir una distancia de 2 + 5 y tendremos el centro E. Con radio 5 dibujar un arco.
7 – Para el arco de centro F se pueden plantear cuatro casos, elige el que más fácil sea para ti :
7a – Hallar las circunferencias tangentes a dos circunferencias (las de centros D y E) y que pasan por un punto (el punto de tangencia G de la circunferencia D en la recta separada 13).
Puedes ver varios casos resueltos en https://trazoide.com/enlaces_y_tangencias.html#desconociendo-RADIO bajo el título «Circunferencia, Circunferencia, Punto – CCP».
7b – Hallar las circunferencias tangentes a una circunferencia (la de centro E), a una recta (la separada 13) y que pasen por un punto (el punto de tangencia G de la circunferencia de centro D con la recta).
7c – Hallar las circunferencias tangentes a una circunferencia (la de centro D), a una recta (la separada 13) y que pasan por un punto (el punto de tangencia G de la circunferencia D en la recta separada 13).
7d – Hallar las circunferencias tangentes a dos circunferencias (las de centros D y E) y a una recta (la separada 13). Este caso se resuelve igual que el del apartado 7.
Inicio > Geometría plana > Enlaces y tangencias
Inicio > Sistema axonométrico > Intersección de cuerpos en axonométrico | | Vídeos sobre secciones
El cuadrilátero ABCD es la base de una pirámide con vértice en el punto V y altura 57 mm. El triángulo EFG es la base de un prisma oblicuo cuyas generatrices son paralelas a la recta r.
Dibujar en sistema axonométrico isométrico la intersección de ambas figuras, especificando partes vistas y ocultas. Indicar el tipo de intersección que se produce.
La colocación de las piezas respecto a los ejes del sistema axonométrico se especifica mediante la proyección horizontal del eje x y el eje y.
SOLUCIÓN
1 – Dibujar las perspectivas de la pirámide y del prisma.
2 – Por la proyección principal del vértice de la pirámide, V, se dibuja una paralela a las aristas del prisma, //R.
3 – Por la proyección secundaria del vértice de la pirámide, v, se dibuja una proyección de las aristas del prisma, //r.
4 – Donde ambas se corten, Txy, es el punto por el que pasarán todas las trazas de los planos que necesitamos.
5 – Se dibuja la traza de un plano, p1, que pase por Txy y por un vértice del prisma, por ejemplo G, y que corte a la base de la pirámide.
6 – La traza, p1, corta a la base de la pirámide en dos puntos, h e i, y se unen con el vértice de la pirámide, V.
7 – Donde se corten hV e iV con la arista G son los puntos 1 y 2 de intersección de los dos cuerpos.
8 – Se debe repetir con el resto de vértices de la base del prisma, pero el plano que pasa por F no corta a la base de la pirámide por dos centésimas de milímetro. Si dibujas a mano parecerá que sí la corta. El plano que pasa por E no corta a la base de la pirámide.
9 – Repetir con planos que pasen por los vértices de la base de la pirámide, A, B, C y D.
Inicio > Sistema axonométrico > Intersección de cuerpos en axonométrico | | Vídeos sobre secciones
Intersección cuerpos isométrico – 976
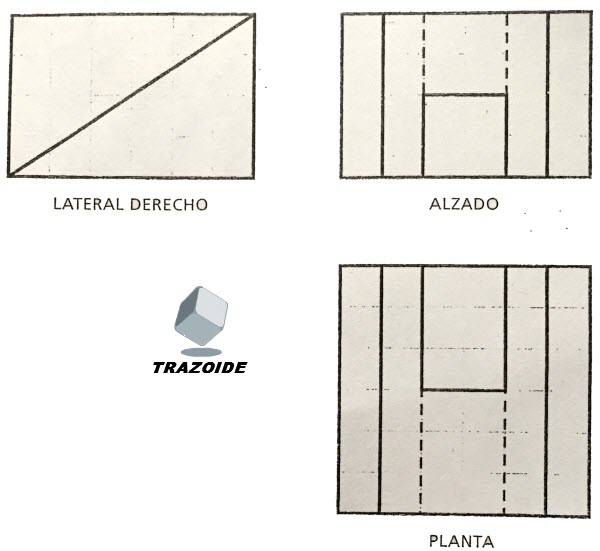
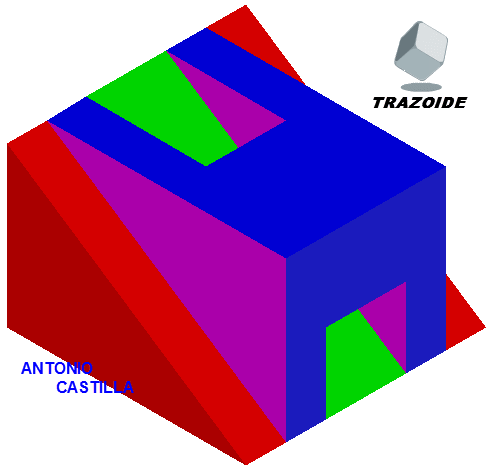
Trazar en perspectiva frontal, un hexaedro o cubo de arista 30 mm con una diagonal vertical.
SOLUCIÓN
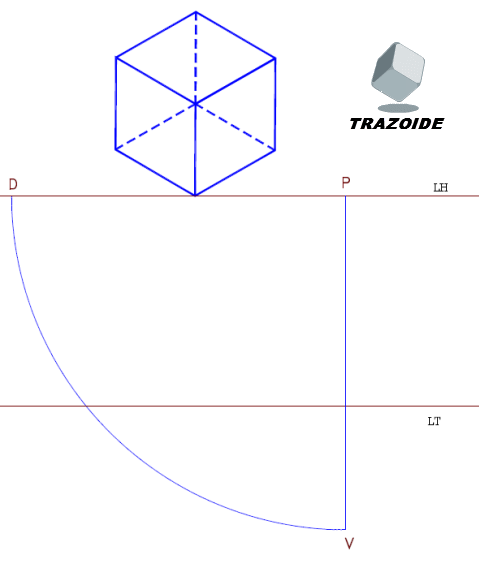
I – Conocido el valor de la arista del cubo, «a», se halla el valor de la diagonal del cubo, Di.
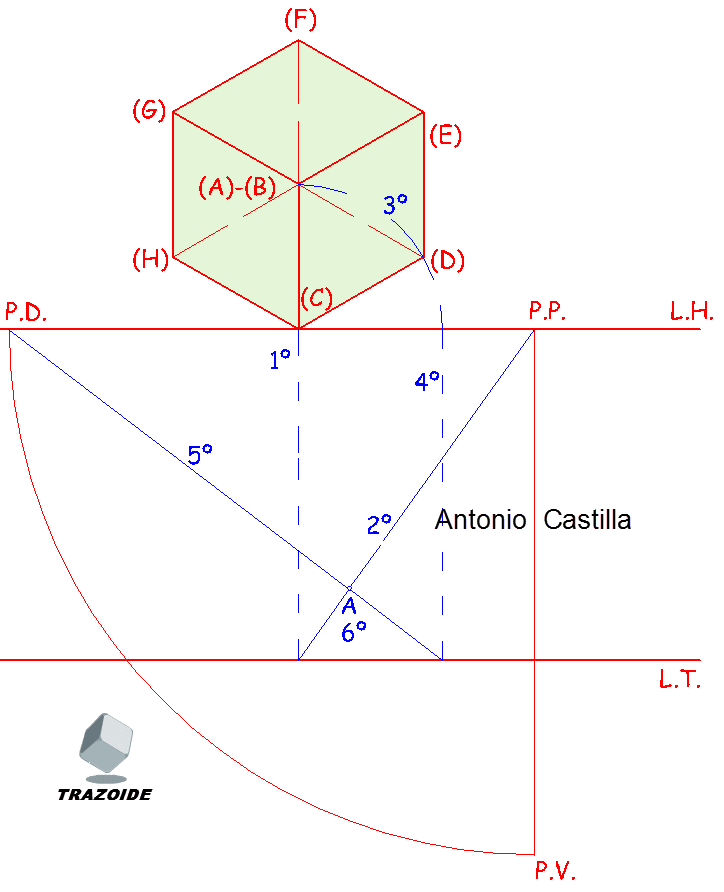
II – El vértice A es el vértice en el que se apoya el cubo sobre el plano geometral o plano horizontal de proyección. Hallamos su proyección cónica, A.
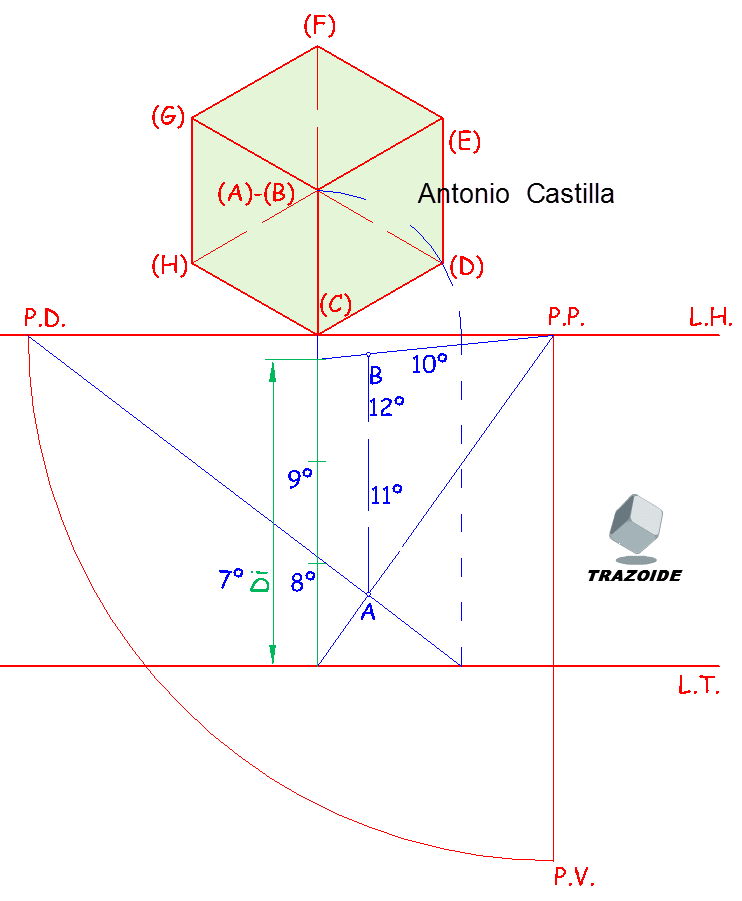
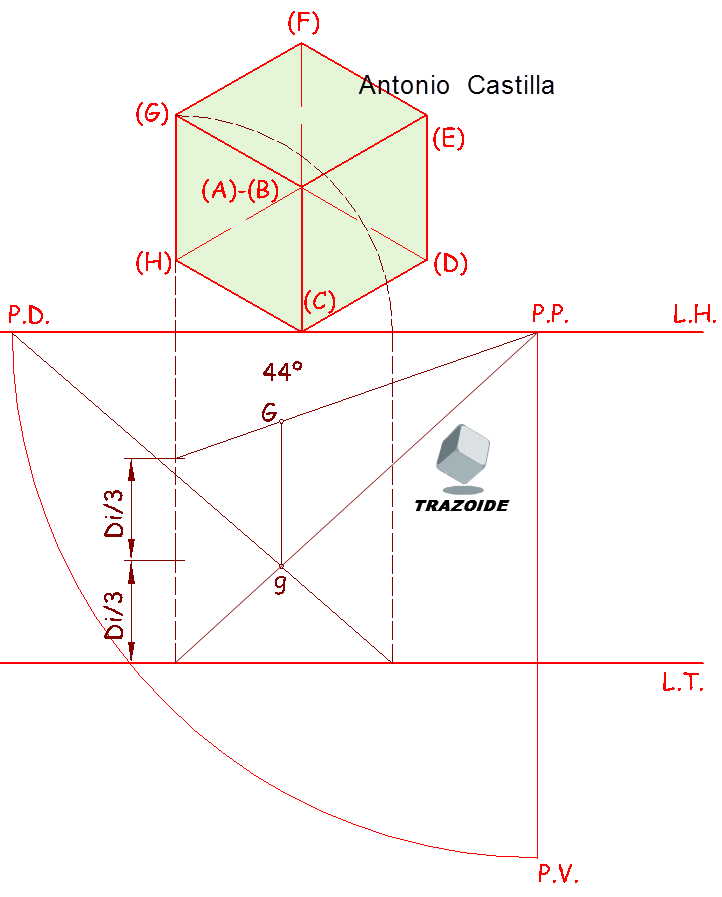
III – El vértice B es el vértice opuesto al vértice A y que está sobre la diagonal que colocaremos vertical. Para ello colocaremos la medida de la diagonal del cuerpo, Di (paso 7º). Los pasos 8º y 9º consisten en dividir la diagonal en tres partes iguales, que aunque para este punto no es necesario lo utilizaremos en los siguientes pasos.
IV – Seguimos con el vértice C, que como está en el plano del cuadro se puede determinar directamente.
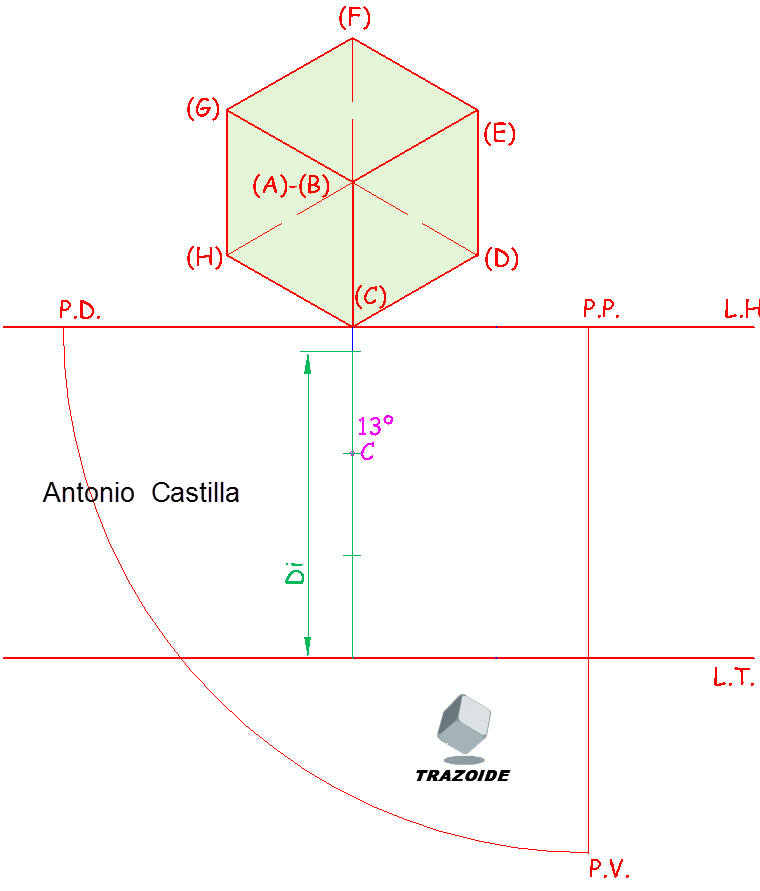
Una aclaración, los vértices de un cubo con una diagonal vertical tiene los demás vértices a una altura de un tercio (Di/3) y de dos tercios (2Di/3) de la diagonal del cubo, alternativamente. Así, el vértice C está a 2/3, D a 1/3, E a 2/3, F a 1/3, etc.
V – Los demás vértices, como F, se determinan de la misma forma que los anteriores.
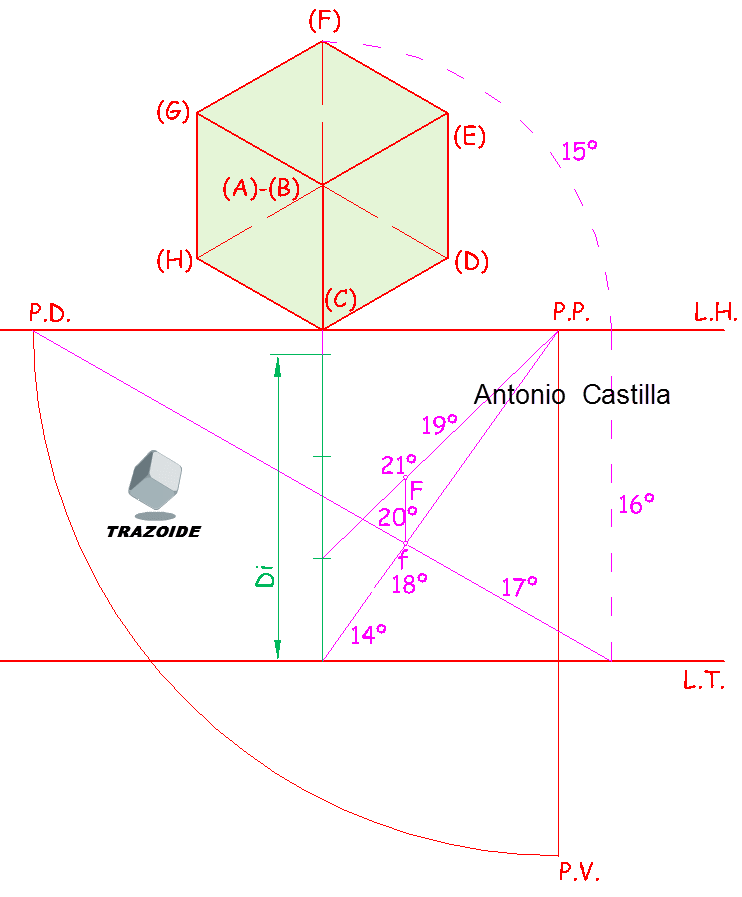
VI – He seguido el mismo procedimiento para todos, como el próximo D, para asentar el procedimiento, aunque se pueden utilizar otros procedimientos que pueden simplificar en, algunos casos, el trabajo.
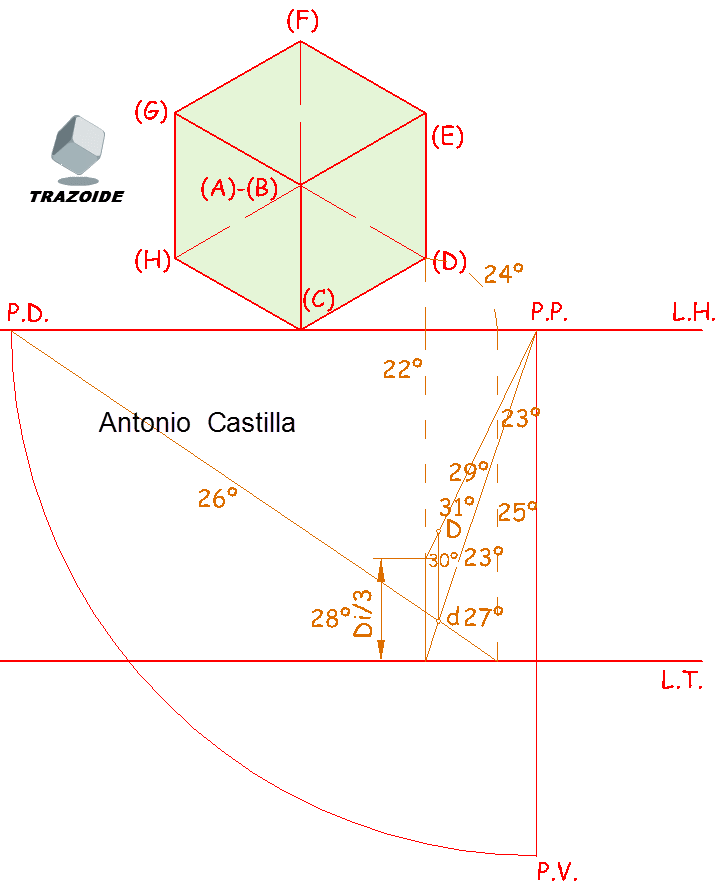
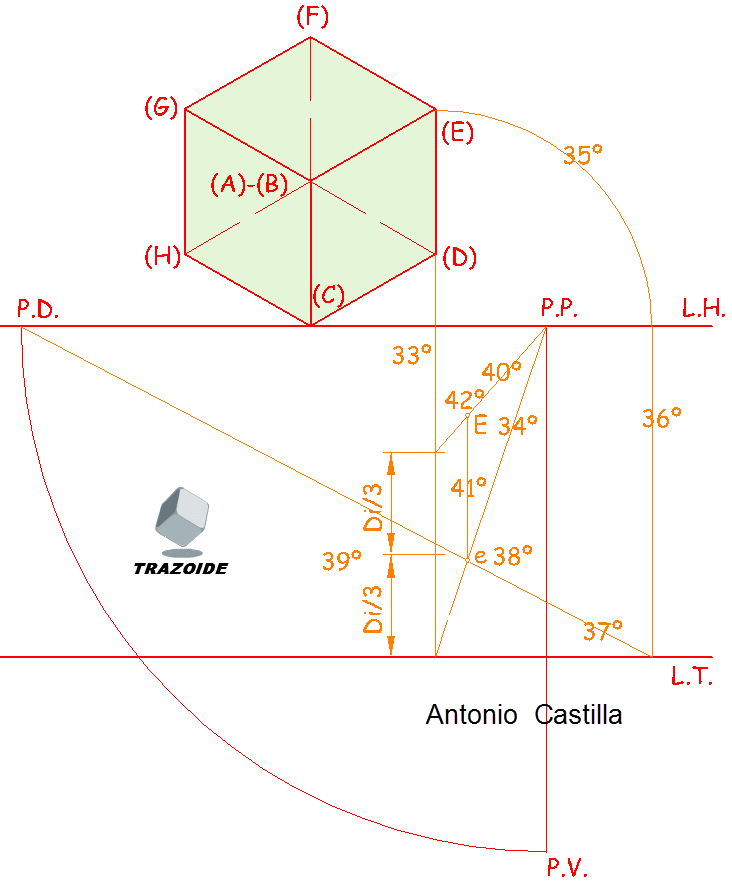
VII – Sigo con el vértice E.
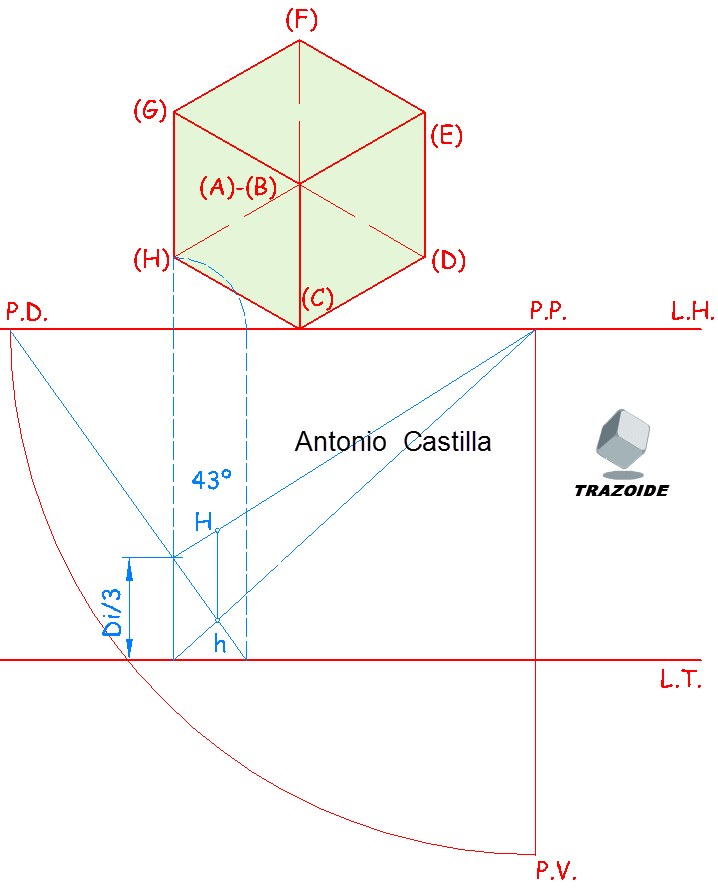
VIII – Paso al vértice H. Ya no específico cada paso por ser los mismos.
IX – El último vértice, G.
XI – Para unir los puntos, se une el vértice inferior, A, con los que están a 1/3, D, F y H.
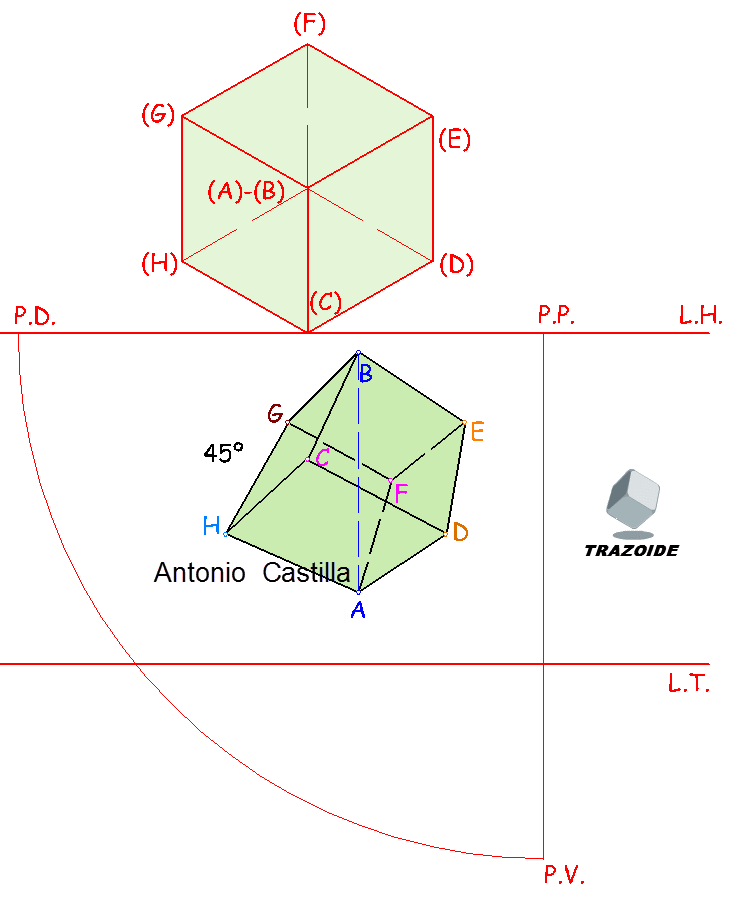
Después unimos el vértice superior, B, con los vértices que están a 2/3, C, E y G.
Por último, se unen los vértices que estaban a 1/3 y 2/3 entre sí, siguiendo el mismo orden que tienen en su planta de forma hexagonal, es decir, C con D, d con E, E con F, etc.
Inicio > Perspectiva cónica | |
perspectiva CÓNICA – 995
Inicio > Normalización > Vistas | | Vídeos sobre vistas
Completar las vistas de una pieza a la que le faltan aristas.
SOLUCIÓN
Esta es la perspectiva isométrica :
Una animación automática :
Esta es la vista interactiva :
En el perfil solo falta una línea (en azul) :
<<< PROBLEMA ANTERIOR – – – – – PROBLEMA SIGUIENTE >>>
Inicio > Normalización > Vistas | | Vídeos sobre vistas
vistas-964