Inicio > Sistema diédrico > Abatimiento
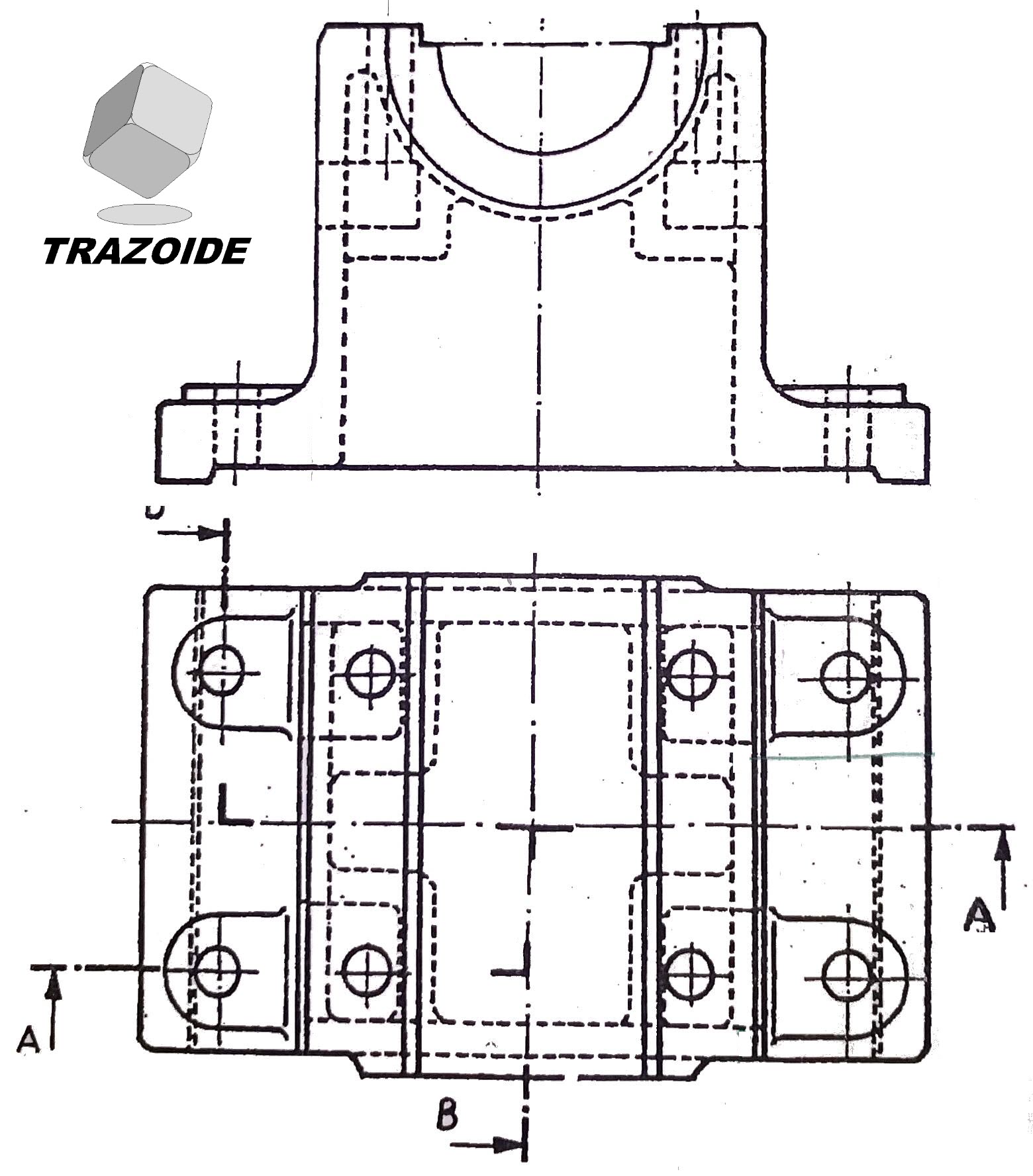
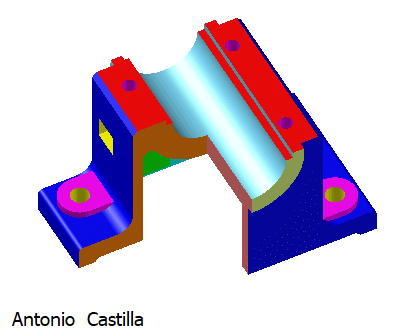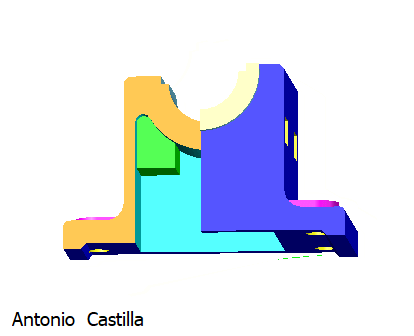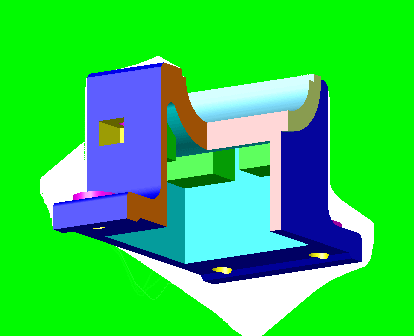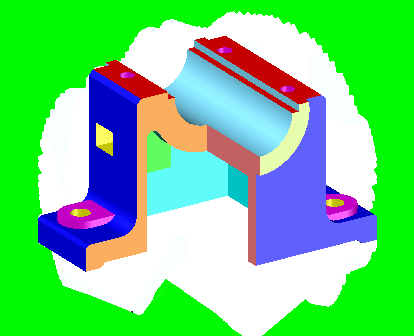
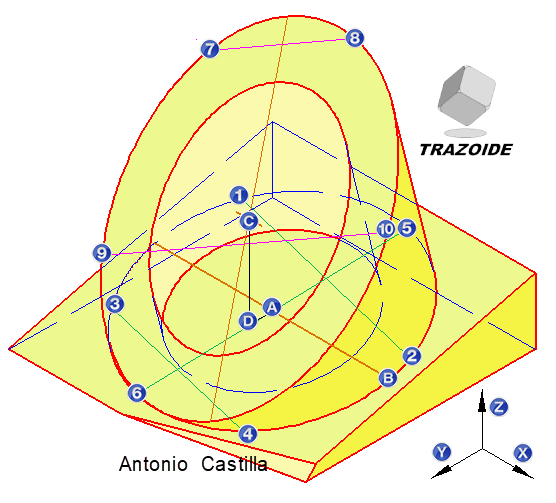
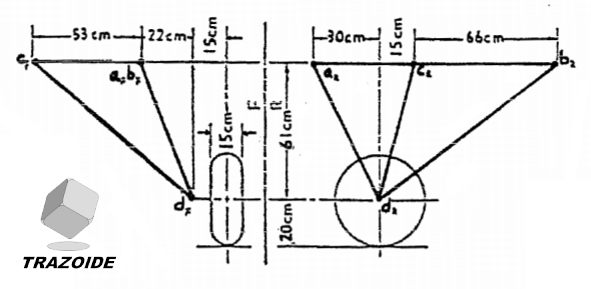
La figura adjunta muestra un tren de aterrizaje, tipo trípode, de un avión.
Determinar:
– La verdadera magnitud y los ángulos que forman cada dos montantes.
– El ángulo de inclinación de cada uno de los montantes con el plano horizontal.
Cotas en centímetros.

SOLUCIÓN
Como siempre, hay varias formas de hacerlo. Las describo :
OPCIÓN I – Mediante abatimiento sobre el plano horizontal de proyección.
Se hallan las trazas del plano y se abate alrededor de ellas.
En este caso es un sistema no adecuado debido a que debes hallar todas las trazas y abatir todos los puntos. Mucho trabajo.
OPCIÓN II – Mediante abatimiento sobre un plano horizontal que pasa por los anclajes ABC.
Si realizamos una traslación del plano horizontal de proyección y lo situamos sobre los tres puntos del anclaje, ABC, tenemos una serie de ventajas :
– Las trazas de los planos coinciden con los segmentos AB, BC y AC, lo que nos ahorra mucho trazado.
– Solo hay que abatir el punto D, ya que los otros puntos, A-B-C, al encontrarse sobre el plano del abatimiento ya están abatidos.
– Las diferencias de cota son más pequeñas, lo que reduce el tamaño del papel necesario.
OPCIÓN III – Abatimientos en la proyección vertical sin necesidad de dibujar una planta.
Consiste en rebatir (abatir apoyándose en la misma proyección) sobre la proyección vertical. Es decir, los segmentos a’b’, b’c’ y a’c’ se utilizan como charnelas para el abatimiento. Tiene la ventaja de que no necesita dibujar la planta y menos espacio en el papel. Tiene la desventaja de que puede resultar más confuso.
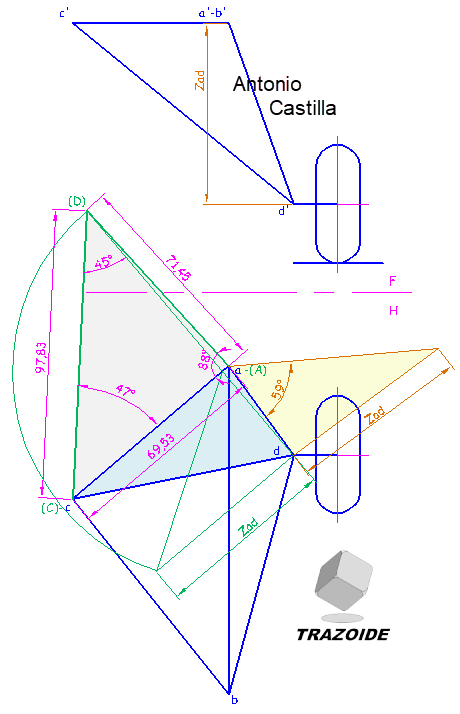
Comento los pasos desarrollados de la segunda opción:
1 – La cara ABC por ser paralela al plano horizontal ya está en verdadera magnitud.
2 – Resolveré solo la cara ACD, las demás caras se resuelven de igual forma.
La arista AC se considera la charnela (o traza del plano) para realizar el abatimiento. A y C ya están abatidos.
3 – Se toma la diferencia de cota, Zad, entre d’ y el plano horizontal que utilizamos para el abatimiento, a’b’c’.
4 – Desde la proyección horizontal, d, se dibuja (en verde) una paralela y una perpendicular a la charnela, ac.
5 – Sobre la paralela se lleva la diferencia de cota Zad (en verde) y con centro donde la perpendicular toca a la charnela se traza un arco que corta a la perpendicular en el abatimiento del punto, (D).
6 – Unir los tres puntos abatidos del plano, (A)-(C)-(D). En este abatimiento se pueden medir (en magenta) tanto las longitudes de las barras como los ángulos entre ellas.
7 – Para determinar el ángulo de inclinación de cada uno de los montantes con el plano horizontal se toma la diferencia de cota, Zad, de sus extremos.
8 – En la proyección horizontal se traza (en marrón) una perpendicular al segmento (no confundir con la perpendicular a la charnela, esta es perpendicular a la proyección horizontal). Solo he determinado el ángulo de la barra AD, para las demás aplicar el mismo procedimiento.
9 – Sobre la perpendicular llevar la diferencia de cota, Zad (en marrón) y unir con su otro extremo (triángulo relleno de color amarillo).
10 – El ángulo medido entre la hipotenusa del triángulo y la proyección horizontal del segmento es el ángulo formado por el montante y el plano horizontal de proyección.
Inicio > Sistema diédrico > Abatimiento | | Vídeos sobre abatimientos






abatimientos – 951