Elementos mecánicos.
Eslabón – Manivela – Balancín – Biela – Anclaje (Tierra, Fijación)
Autor: Administrador
Eslabón
Eslabón.
- En una cadena, un eslabón es cada uno de los anillos o elementos que la forman.
- En un mecanismo o cadena cinemática, un eslabón es el cuerpo rígido que posee al menos dos nodos o puntos de unión con otros eslabones y sirve para transmitir el movimiento de unos a otros. Según el número de nodos los eslabones pueden ser binarios (de dos nodos), ternarios (de tres nodos) o cuaternarios (de cuatro nodos). Según el tipo de movimiento pueden ser manivelas, balancines, bielas anclajes.
Corte de chumacera
Inicio > Normalización > Cortes | | Vídeos sobre cortes
A partir de las vistas diédricas que se adjuntan, dibuje los cortes AA y BB.
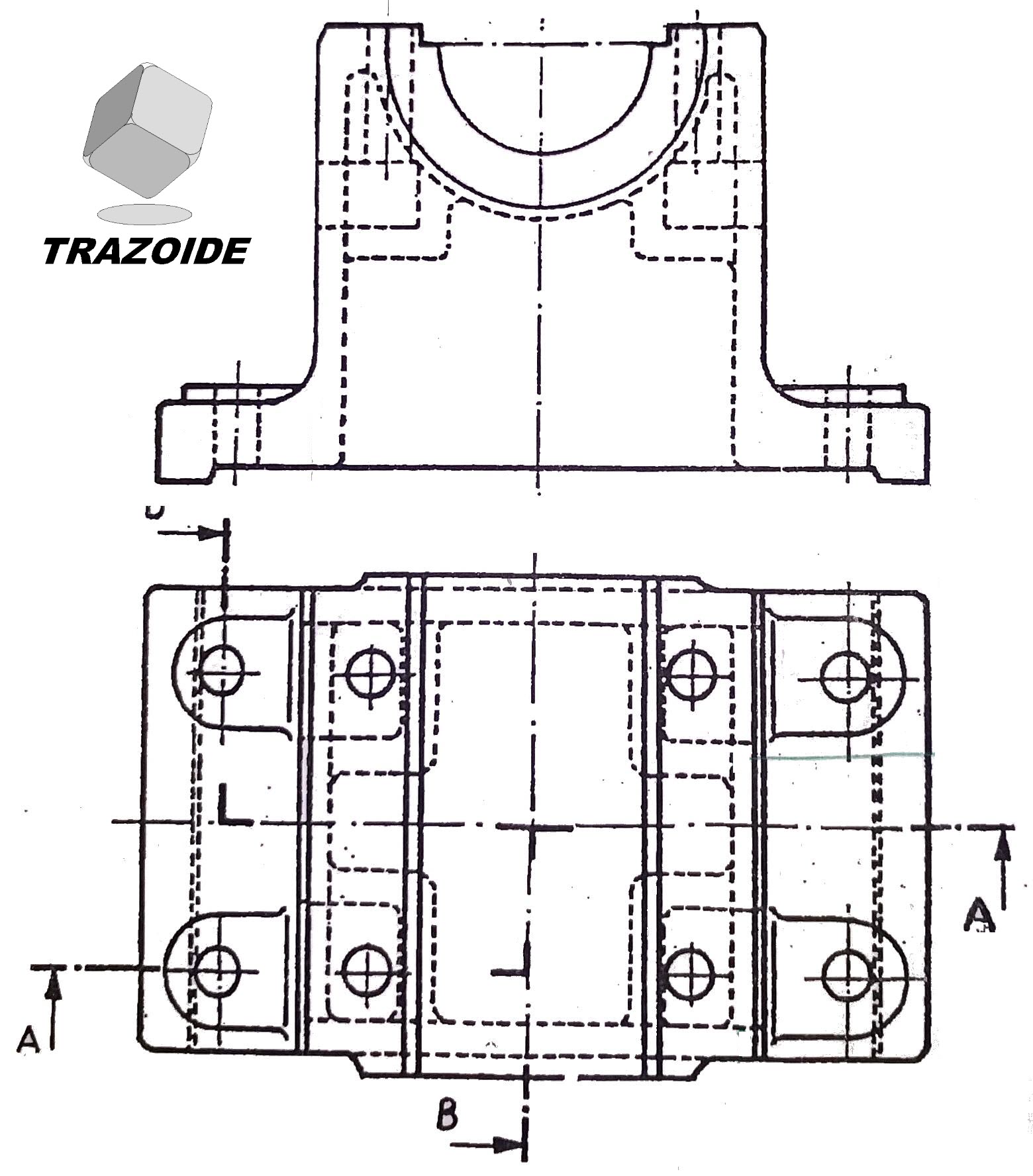
SOLUCIÓN
La dificultad viene de que hay varias aristas que coinciden.
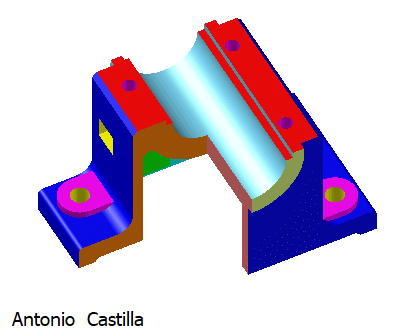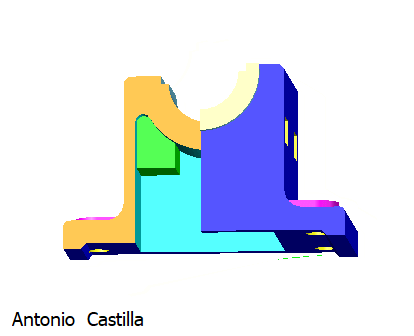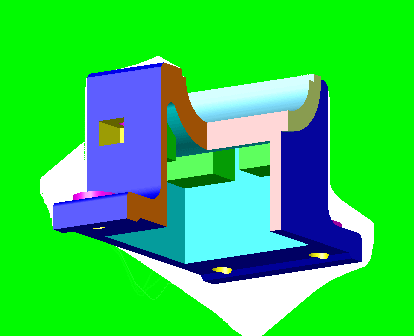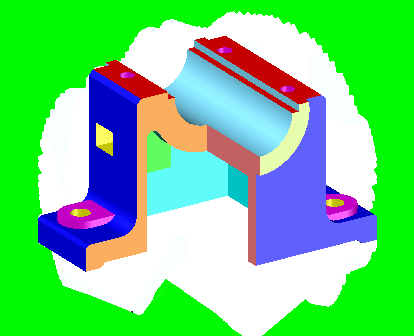
Estas imágenes te ayudaran a visualizar la pieza. No he dibujado los redondeos pequeños para simplificar.
Las siguientes figuras ayudaran al visionando la pieza en el espacio.
Los objetos son interactivos se pueden mover con el ratón o con los dedos en pantallas táctiles :
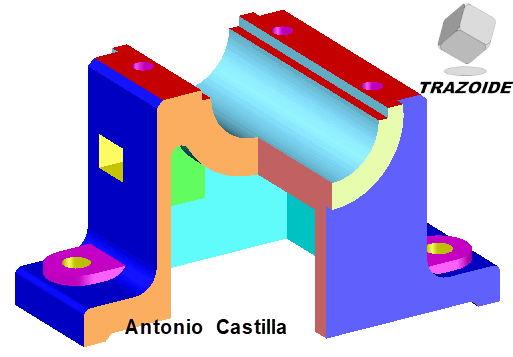
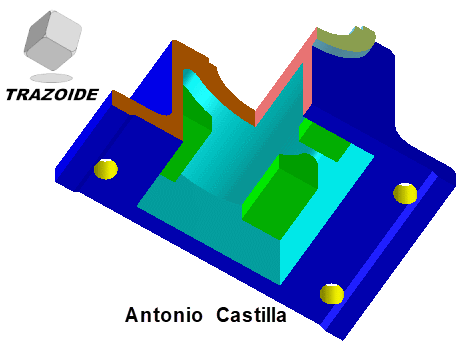
En estas imágenes le he hecho un cuarto de corte para que se vea tanto el exterior como el interior:
Inicio > Normalización > Cortes | | Vídeos sobre cortes
Vistas diédricas de un cilindro en un plano inclinado – UNED
Inicio > Normalización > Vistas | | Vídeos sobre vistas
Selectividad Uned.
Dada la pieza representada en la figura dibujar, a lápiz y a la escala más apropiada al papel disponible, las seis vistas de la misma en sistema diédrico europeo.
SOLUCIÓN
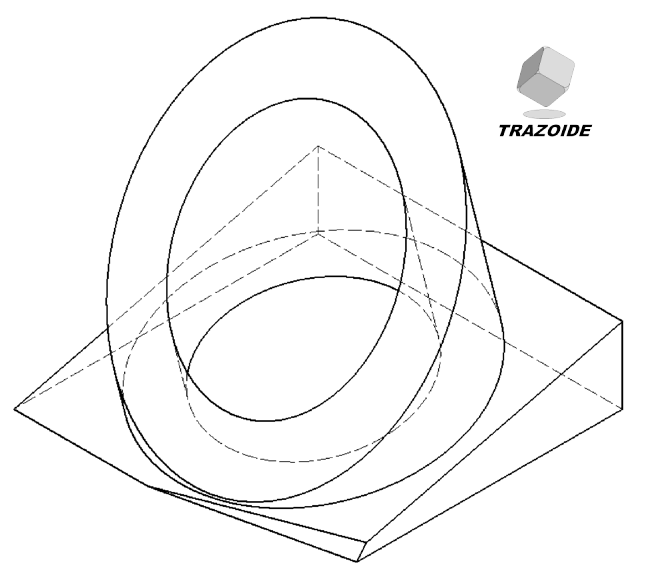
1 – Solo se pueden medir aquellas longitudes que sean paralelas a los ejes de la perspectiva, X-Y-Z.
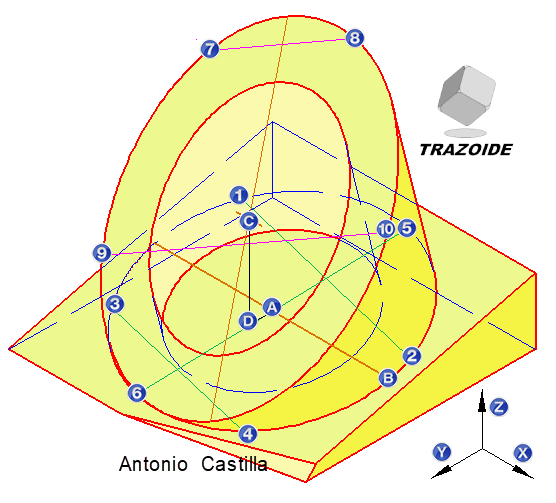
2 – Para determinar el centro de la elipse que se apoya en la cara oblicua se dibuja una cuerda cualquiera 1-2 y otra paralela a ella, 3-4, en cualquier posición. Puedes ver el procedimiento explicado en https://trazoide.com/elipse_979/
3 – Se unen los puntos medios de ambas cuerdas, 1-2 y 3-4, y el segmento resultante se prolonga hasta tocar a la elipse, 5-6.
4 – El punto medio, A, de la última cuerda, 5-6, es el centro de la elipse.
5 – Por dicho centro, A, se traza una paralela al eje X hasta cortar a la elipse, B. La distancia desde el centro de la elipse, A, hasta uno de los extremos, B, es el radio de la circunferencia en verdadera magnitud.
6 – El centro de las elipses superiores se halla de la misma forma. Dibujar una cuerda cualquiera, 7-8, y una paralela a ella, 9-10. Unir sus puntos medios y prolongarlos hasta tocar a la elipse. El punto medio de esta cuerda es el centro C.
7 – El eje del cilindro lo supondremos ortogonal a la cara oblicua. Para hallar su longitud se unen los centros de ambas elipses, A y C, con dos paralelas a los ejes Y y Z.
Inicio > Normalización > Vistas | | Vídeos sobre vistas
Longitudes de los montantes de un tren de aterrizaje
Inicio > Sistema diédrico > Abatimiento
La figura adjunta muestra un tren de aterrizaje, tipo trípode, de un avión.
Determinar:
– La verdadera magnitud y los ángulos que forman cada dos montantes.
– El ángulo de inclinación de cada uno de los montantes con el plano horizontal.
Cotas en centímetros.
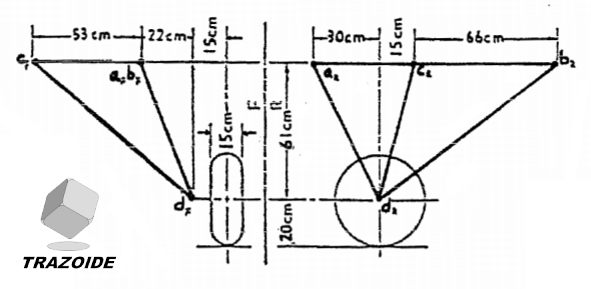
SOLUCIÓN
Como siempre, hay varias formas de hacerlo. Las describo :
OPCIÓN I – Mediante abatimiento sobre el plano horizontal de proyección.
Se hallan las trazas del plano y se abate alrededor de ellas.
En este caso es un sistema no adecuado debido a que debes hallar todas las trazas y abatir todos los puntos. Mucho trabajo.
OPCIÓN II – Mediante abatimiento sobre un plano horizontal que pasa por los anclajes ABC.
Si realizamos una traslación del plano horizontal de proyección y lo situamos sobre los tres puntos del anclaje, ABC, tenemos una serie de ventajas :
– Las trazas de los planos coinciden con los segmentos AB, BC y AC, lo que nos ahorra mucho trazado.
– Solo hay que abatir el punto D, ya que los otros puntos, A-B-C, al encontrarse sobre el plano del abatimiento ya están abatidos.
– Las diferencias de cota son más pequeñas, lo que reduce el tamaño del papel necesario.
OPCIÓN III – Abatimientos en la proyección vertical sin necesidad de dibujar una planta.
Consiste en rebatir (abatir apoyándose en la misma proyección) sobre la proyección vertical. Es decir, los segmentos a’b’, b’c’ y a’c’ se utilizan como charnelas para el abatimiento. Tiene la ventaja de que no necesita dibujar la planta y menos espacio en el papel. Tiene la desventaja de que puede resultar más confuso.
Comento los pasos desarrollados de la segunda opción:
1 – La cara ABC por ser paralela al plano horizontal ya está en verdadera magnitud.
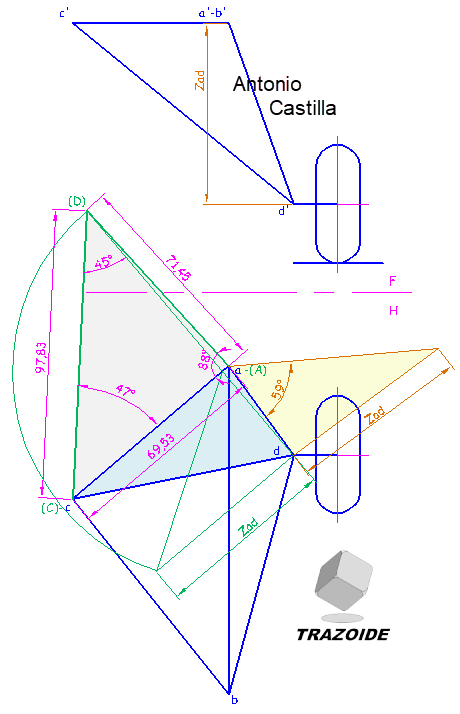
2 – Resolveré solo la cara ACD, las demás caras se resuelven de igual forma.
La arista AC se considera la charnela (o traza del plano) para realizar el abatimiento. A y C ya están abatidos.
3 – Se toma la diferencia de cota, Zad, entre d’ y el plano horizontal que utilizamos para el abatimiento, a’b’c’.
4 – Desde la proyección horizontal, d, se dibuja (en verde) una paralela y una perpendicular a la charnela, ac.
5 – Sobre la paralela se lleva la diferencia de cota Zad (en verde) y con centro donde la perpendicular toca a la charnela se traza un arco que corta a la perpendicular en el abatimiento del punto, (D).
6 – Unir los tres puntos abatidos del plano, (A)-(C)-(D). En este abatimiento se pueden medir (en magenta) tanto las longitudes de las barras como los ángulos entre ellas.
7 – Para determinar el ángulo de inclinación de cada uno de los montantes con el plano horizontal se toma la diferencia de cota, Zad, de sus extremos.
8 – En la proyección horizontal se traza (en marrón) una perpendicular al segmento (no confundir con la perpendicular a la charnela, esta es perpendicular a la proyección horizontal). Solo he determinado el ángulo de la barra AD, para las demás aplicar el mismo procedimiento.
9 – Sobre la perpendicular llevar la diferencia de cota, Zad (en marrón) y unir con su otro extremo (triángulo relleno de color amarillo).
10 – El ángulo medido entre la hipotenusa del triángulo y la proyección horizontal del segmento es el ángulo formado por el montante y el plano horizontal de proyección.
<<< PROBLEMA ANTERIOR – – – – – PROBLEMA SIGUIENTE >>>
Inicio > Sistema diédrico > Abatimiento | | Vídeos sobre abatimientos
abatimientos – 951
Vista desarrollada
Vista desarrollada
En general, la vista desarrollada de un cuerpo es la representación de la superficie de un cuerpo extendida sobre un plano.
Las vistas desarrolladas se utilizan en calderería para recortar una figura sobre chapa y después de plegarla obtener el cuerpo deseado.
A las vistas desarrolladas también se les conoce como desarrollos.
Sinónimos :
Desarrollo – Vista desarrollada – Red
Horqueta
Horqueta.
Es la pieza mecánica formado por tres brazos, uno principal del que parte otros dos iguales y paralelos formando un hueco entre ellos. Es parecido a la letra Y. Se utiliza para situar una rueda con su eje sujeta entre los dos brazos siendo el tercer brazo desigual el que se utiliza como eje para cambiar la orientación de la rueda, es la pieza que sujeta la rueda direccional en motocicletas o bicicletas. También se utiliza para empujar un engranaje o un collarín y que deslice sobre su eje de giro, es muy utilizado para engranar engranajes en una caja de cambios de un automóvil o para empujar el collarín de empuje en un embrague de discos.
En España se la conoce como horquilla.
Horquilla
Horquilla.
Es la pieza mecánica formado por tres brazos, uno principal del que parte otros dos iguales y paralelos formando un hueco entre ellos. Es parecido a la letra Y. Se utiliza para situar una rueda con su eje sujeta entre los dos brazos siendo el tercer brazo desigual el que se utiliza como eje para cambiar la orientación de la rueda, es la pieza que sujeta la rueda direccional en motocicletas o bicicletas. También se utiliza para empujar un engranaje o un collarín y que deslice sobre su eje de giro, es muy utilizado para engranar engranajes en una caja de cambios de un automóvil o para empujar el collarín de empuje en un embrague de discos.
En Latinoamérica se la conoce como horqueta.
Selectividad Andalucía – Isométrico 8
Inicio > Sistema axonométrico > Isométrica || Vídeos sobre el sistema isométrico
Selectividad de Andalucía.
Dados alzado, planta y perfil de un cuerpo a escala 2:3, según el método de representación del primer diedro de proyección, se pide:
Representar su perspectiva isométrica a escala 1:1 considerando los ejes dados.
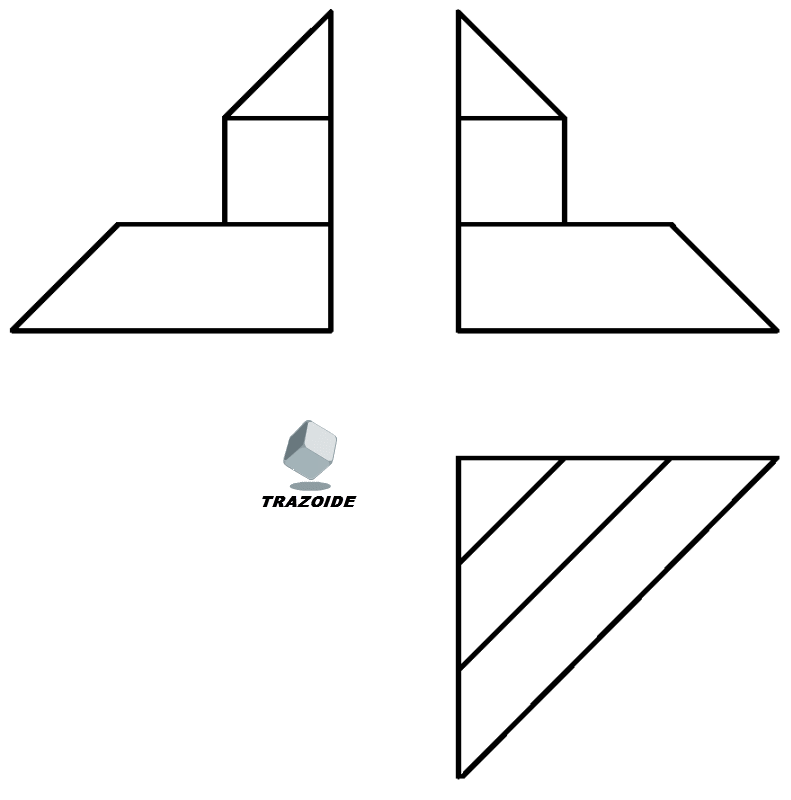
SOLUCIÓN
Las siguientes figuras ayudaran al visionando la pieza en el espacio.
Los objetos son interactivos se pueden mover con el ratón o con los dedos en pantallas táctiles :
<<< PROBLEMA ANTERIOR – – – – – PROBLEMA SIGUIENTE >>>
Inicio > Sistema axonométrico > Isométrica
isométrica – 914
Selectividad Andalucía – Isométrico 6
Inicio > Sistema axonométrico > Isométrica || Vídeos sobre el sistema isométrico
Selectividad de Andalucía.
Dados alzado, planta y perfil de un cuerpo a escala 2:3, según el método de representación del primer diedro de proyección, se pide:
Dibujar la perspectiva isométrica a escala 4:3 según los ejes dados.
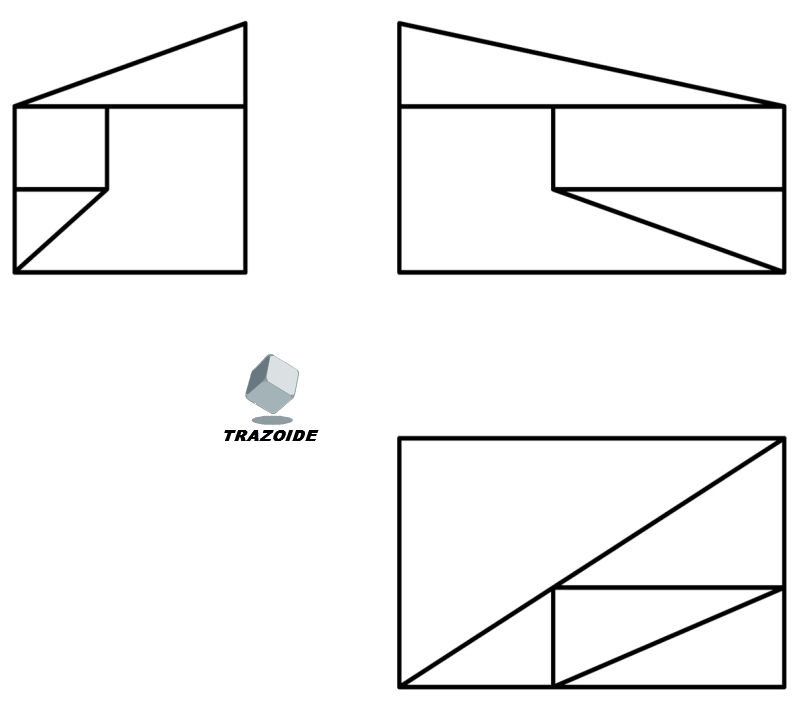
SOLUCIÓN
Las siguientes figuras ayudaran al visionando la pieza en el espacio.
Los objetos son interactivos se pueden mover con el ratón o con los dedos en pantallas táctiles :
<<< PROBLEMA ANTERIOR – – – – – PROBLEMA SIGUIENTE >>>
Inicio > Sistema axonométrico > Isométrica
isométrica – 913