Me gustaría saber :
A) cómo se hace la intersección de una recta con un plano oblicuo cuando la recta se quiere meter en un plano proyectante y no corta a la línea de tierra ninguna de sus proyecciones.
Y también :
B) cúal es la intersección de un plano oblicuo con una recta horizontal cuando la proyeccion horizontal de la recta no corta a la L.T.
interseccion recta plano
Reglas del Foro
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
 BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)
BUSCA EN LOS ÍNDICES antes de preguntar (pulsa aquí)- Escribir los enunciados completos, incluir una imagen y lo que tienes hecho hasta ahora.
 El usuario que no conteste o no dé las gracias después de responderle será expulsado
El usuario que no conteste o no dé las gracias después de responderle será expulsado
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
Para el primer caso hay varias formas de hacerlo. Te comento un par de ellas y tu eliges cual te viene mejor.
Determinación de la intersección de una recta con un plano, si las proyecciones de la recta cortan a la línea de tierra fuera de los límites del papel
OPCIÓN I
1 - Hacer un cambio de plano con la segunda línea de tierra perpendicular a la traza horizontal del plano
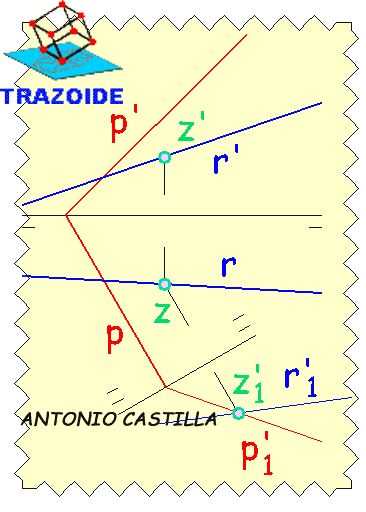
2 - Cambiar de plano tanto la recta como el plano
3 - En el cambio de plano la intersección de ambos es inmediata, punto Z
4 - Deshacer el cambio de plano del punto Z
Para el primer caso hay varias formas de hacerlo. Te comento un par de ellas y tu eliges cual te viene mejor.
Determinación de la intersección de una recta con un plano, si las proyecciones de la recta cortan a la línea de tierra fuera de los límites del papel
OPCIÓN I
1 - Hacer un cambio de plano con la segunda línea de tierra perpendicular a la traza horizontal del plano

2 - Cambiar de plano tanto la recta como el plano
3 - En el cambio de plano la intersección de ambos es inmediata, punto Z
4 - Deshacer el cambio de plano del punto Z
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
Determinación de la intersección de una recta con un plano, si las proyecciones de la recta cortan a la línea de tierra fuera de los límites del papel
OPCIÓN II
5 - Se hace que la recta R esté contenida en un plano proyectante, q'.
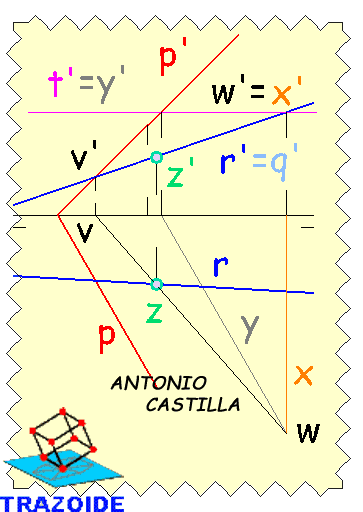
6 - Donde corte a la traza vertical del plano dado, punto V, es un punto de la intersección del plano dado P con el que contiene a la recta, Q.
7 - Se dibuja un plano auxiliar (horizontal, por ejemplo), T.
8 - Se determina la intersección del plano auxiliar T con el plano proyectante Q, recta de punta X.
9 - Se halla la intersección del plano auxiliar T con el plano dado P, recta horizontal Y.
10 - Se determina el punto común a los tres planos, P, Q y T, que está donde se corten las dos intersecciones entre planos, X e Y, dando el punto común W.
11 - El punto W y el punto V pertenecen a los planos P y Q, por lo que forman la intersección entre los dos planos.
12 - Por último, donde esta intersección V-W, corte a la recta dada, R, es el punto intersección del plano P con la recta R (punto Z).
13 - Si el punto V tampoco es posible, se recurre a otro plano horizontal o frontal para hallar un segundo punto que nos dé la intersección entre el plano P y el Q.
OPCIÓN II
5 - Se hace que la recta R esté contenida en un plano proyectante, q'.

6 - Donde corte a la traza vertical del plano dado, punto V, es un punto de la intersección del plano dado P con el que contiene a la recta, Q.
7 - Se dibuja un plano auxiliar (horizontal, por ejemplo), T.
8 - Se determina la intersección del plano auxiliar T con el plano proyectante Q, recta de punta X.
9 - Se halla la intersección del plano auxiliar T con el plano dado P, recta horizontal Y.
10 - Se determina el punto común a los tres planos, P, Q y T, que está donde se corten las dos intersecciones entre planos, X e Y, dando el punto común W.
11 - El punto W y el punto V pertenecen a los planos P y Q, por lo que forman la intersección entre los dos planos.
12 - Por último, donde esta intersección V-W, corte a la recta dada, R, es el punto intersección del plano P con la recta R (punto Z).
13 - Si el punto V tampoco es posible, se recurre a otro plano horizontal o frontal para hallar un segundo punto que nos dé la intersección entre el plano P y el Q.
- Antonio Castilla
- USUARIO

- Mensajes: 4239
- Registrado: Mar, 03 Jun 2008, 18:12
.
El segundo caso que planteas es un caso normal, lo que ocurre es que el plano proyectante es además horizontal
Determinación de la intersección de una recta horizontal con un plano, si la proyección horizontal de la recta no corta a la línea de tierra dentro de los límites del papel
14 - Considera la recta contenida en un plano proyectante, cuya traza vertical coincide con la proyección vertical de la recta (el plano es horizontal).
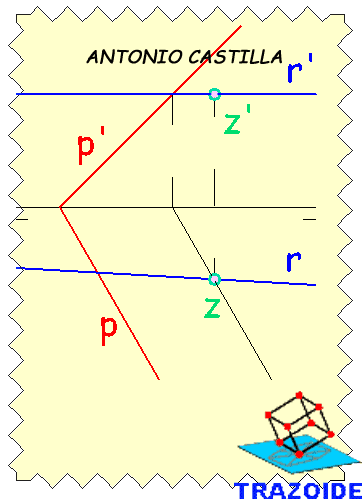
15 - Se halla la intersección del plano horizontal con el dado, dando una recta horizontal.
16 - Donde esta recta corte a la proyección horizontal de la recta dada es el punto de intersección buscado, Z.
También se puede aplicar un cambio de plano como se explicó en el caso anterior.
El segundo caso que planteas es un caso normal, lo que ocurre es que el plano proyectante es además horizontal
Determinación de la intersección de una recta horizontal con un plano, si la proyección horizontal de la recta no corta a la línea de tierra dentro de los límites del papel
14 - Considera la recta contenida en un plano proyectante, cuya traza vertical coincide con la proyección vertical de la recta (el plano es horizontal).

15 - Se halla la intersección del plano horizontal con el dado, dando una recta horizontal.
16 - Donde esta recta corte a la proyección horizontal de la recta dada es el punto de intersección buscado, Z.
También se puede aplicar un cambio de plano como se explicó en el caso anterior.
¿Quién está conectado?
Usuarios navegando por este Foro: Google [Bot] y 2 invitados

