Mes: octubre 2014

Ejercicios de PIRÁMIDES en diédrico resueltos – 999

Inicio > Sistema diédrico > Pirámides

1 – Hallar la intersección de una pirámide hexagonal regular, de 69 mm de altura, con un plano proyectante horizontal (beta) que forma un ángulo de 60 grados con el plano vertical, hacia la izquierda.
2 – Obtener la verdadera magnitud de la sección.
De la pirámide regular se conocen los siguientes datos :
– Está apoyada por su base en un plano proyectante vertical (alfa) que forma 45 grados con el horizontal de proyección a la derecha. El punto de la media base se encuentra en el primer diedro, alejado 46 mm. del plano vertical y situado en el proyectante a 102 mm del punto de intersección de sus trazas (medidos sobre alfa’ )
– Uno de los vértices del hexágono de a base se encuentra en el primer diedro, alejado 69 mm del plano vertical y situado en el proyectante a 126 mm del punto de intersección de sus trazas (medidos sobre alfa’ ) los puntos de intersección de las trazas de los planos alfa y beta se encuentran separados 89 mm.

---

SOLUCIÓN

Esta es la solución :

---

Inicio > Sistema diédrico > Pirámides | |

Inicio > Sistema diédrico > Pirámides

Pirámide conocidos dos puntos de la base y el vértice.

Se ha considerado una pirámide recta de base hexagonal (ver perspectiva adjunta) para la elaboración de patas niveladoras de máquinas. Se pide :

1.- Representar las proyecciones de la entrecara y determinar su magnitud.

2.- Representar el plano determinado por A, B y V.

3.- Representar las proyecciones del centro de la base y determinar la altura de la pirámide.

4.- Representar las proyecciones de la pirámide.

5.- Representar el plano beta determinado por B, X y el punto medio de la altura.

6.- Representar las proyecciones y VM de la sección que origina beta sobre el sólido.

DATOS :

A ( Alejamiento = 11 mm; Cota = – 31 mm; Distancia al margen derecho del formato = 72 mm)

B ( Alejamiento = 67 mm; Cota = 23 mm; Distancia al margen derecho del formato = 78 mm)

C ( Alejamiento = – 36 mm; Cota = 64 mm; Distancia al margen derecho del formato = 159 mm)

El único vértice de la base que se encuentra a dereha de A y B es X.

NOTA : Este ejercicio se resolverá en un formato A4 en posición vertical, representándose la L.T. en horizontal y dividiendo al formato en dos superficies iguales.

---

SOLUCIÓN

Para la determinación de las magnitudes de la pirámide se construirá un hexágono con el valor entre caras de la magnitud AB abatida. Para ello basta con levantar dos líneas a 30º y donde se corten es el centro del hexágono.

De dicho hexágono se determina el valor de su diagonal, la cual se utilizará para dibujar la sección media de la pirámide (ver la figura de análisis), que es un triángulo isósceles de lados iguales a la magnitud VA y VB tomadas del abatimiento.

La altura de la sección media es el valor de la altura de la pirámide.

Si la recta AB fuese vertical (o de punta), la sección ABV sería proyectante a la vez que la base hexagonal también (ver la figura de análisis).

En esa situación la sección VME estará en verdadera magnitud, la cual está formada por cantidades ya averiguadas anteriormente. Si se prefiere se puede trabajar con la sección VOM.

Para ello se debe colocar la recta AB en posición vertical (o de punta), para lo que se recurre a dos cambios de plano. El primer cambio de plano (en verde) con la línea de tierra paralela a la proyección horizontal de AB y la tercera perpendicular (en naranja).

En el último cambio de plano se dibujará la sección VAE (en azul oscuro) en verdadera magnitud, siendo VE el valor de la arista lateral del cono deducida anteriormente y el segmento ME extraído del hexágono que se dibujó en verdadera magnitud anteriormente.
Si por el vértice V1 se hace una perpendicular (en amarillo) al lado A1-E1 se obtiene la altura y el centro de la base, O1.

También se podría haber trabajado con el triángulo VMO y de esa manera obtener directamente la posición del centro.

Se deshace el cambio de plano (líneas azul claro y naranja) del centro, O, de la base. Siendo el plano VEO proyectante en la otra proyección, por lo que el centro O estará sobre la altura del triángulo VAB.

Para las otras proyecciones se lleva la medida correspondiente (s y t).
Las proyecciones del punto E se determinan de la misma forma (en marrón y naranja) que las del centro O (medidas u y v).

Como el hexágono es simétrico y ya se conocen tres vértices, A-B-E, y el centro, O, basta con unir las proyecciones de esos puntos con el centro y llevar esa misma distancia hacia el otro lado (ver la figura de análisis de la parte superior).

Ya solo queda unir los seis vértices de la base entre sí y con el vértice de la pirámide.

 

---

 

Inicio > Sistema diédrico > Pirámides | |

 

Ejercicios de PIRÁMIDES en diédrico resueltos – 997

Inicio > Sistema diédrico > Pirámides

Sobre un plano "alfa"(-30, 30, 30) se apoya una pirámide recta de 60 mm de altura; se sabe que los vértices de la base son los puntos A(0, 20, Z) B(40, 0, Z) C(20, 35, Z).
Hallar:
a) Las proyecciones diédricas de la pirámide.
b) La longitud real de las aristas AB y CV, siendo V el vértice opuesto de la base.

---

SOLUCIÓN

1 – Sitúa el plano.
2 – Sitúa los puntos A, B y C. Para el punto B, la proyección vertical del punto la tienes sobre la traza vertical del plano por tener alejamiento cero. Para los puntos A y C utiliza una recta horizontal o frontal para localizar su otra proyección.
3 – Localiza el baricentro del triángulo ABC en ambas proyecciones.

4 – Por los baricentros levanta rectas perpendiculares a las trazas del plano.
En el siguiente dibujo lo aclaro.

5 – Sobre esa perpendicular y a partir del baricentro tienes que hallar la proyección de la altura de la pirámide, 60 mm. Este es el vértice V.
En el siguiente dibujo pongo los pasos a seguir

6 – Une el vértice V con ABC. Ya tienes la pirámide.
7 – Determinas las distancias que hay entre AB y CV.

---

Inicio > Sistema diédrico > Pirámides | |

Ejercicios de PIRÁMIDES en diédrico resueltos – 996

Inicio > Sistema diédrico > Pirámides

De un hexágono regular ABCDEF de 50 mm de lado se sabe que el lado AB está en el plano horizontal de proyección y sobre la recta que pasa por K(-50, 0, 0) y forma 30º con la línea de tierra. El lado EF está sobre el plano vertical de proyección.
Se pide:
– Dibujar el hexágono
– Dibujar la pirámide regular que lo tiene por base sabiendo que tiene una cara lateral apoyada en el plano horizontal de proyección. Señalar la parte de la pirámide que queda en el primer cuadrante.

---

SOLUCIÓN

1 – Colocar el punto K y desde él trazar una recta que forme 30º con la línea de tierra. Esta es la traza horizontal del plano que contiene al hexágono, p.

2 – Dibujar un hexágono, a1-b1-c1-d1-e1-f1, de lado 50 apoyado en la recta anterior y en cualquier lugar.
3 – Por K trazar una paralela a e1-f1. Esta es la traza vertical del plano abatida, (p’).
4 – Por f1 hacer una paralela a p y donde corte a (p’) es el vértice (F) del hexágono abatido buscado.
5 – Trazar el resto del hexágono abatido, (A)-(B)-(C)-(D)-(E)-(F), por paralelas al primero, a1-b1-c1-d1-e1-f1.
6 – Las proyecciones horizontales de A y B coinciden con sus abatimientos y las verticales están sobre la línea de tierra.
7 – Por (E) y (F) trazar perpendiculares a la traza horizontal del plano, p, y donde corten a la línea de tierra son sus proyecciones horizontales. Para las verticales subir perpendiculares a la línea de tierra y con centro en K y radios hasta los puntos abatidos, (E) y (F), trazar sendos arcos. Donde corten a las verticales son las proyecciones verticales.
8 – Unir las proyecciones de los puntos, B con A, A con F y F con E.
9 – El lado E-D es paralelo al lado A-B y de igual longitud. Por el extremo D una paralela al lado A-F y con su misma longitud se obtiene C. Unir C con B.

---

Inicio > Sistema diédrico > Pirámides | |

Ejercicios de PIRÁMIDES en diédrico resueltos – 995

Inicio > Sistema diédrico > Pirámides

El segmento A(-0.5; 0.4; 4.75) B(-3.5; 3.1; 7.4) es arista lateral de la base de una pirámide regular de base cuadrada cuyo vértice V está situado en el plano P(12; 10; 10) y tiene cota 2 cm. Se pide dibujar la pirámide dando la solución más alta.

---

SOLUCIÓN

Primera parte. Construcción de una cara lateral de la pirámide, ABV

1 – Situar los puntos A, B y el plano P

2 – Trazar una recta horizontal, R, de cota 2 cm situada en el plano P
3 – Dibujar un plano, Q, perpendicular a la recta AB y que pase por su punto medio.
4 – Hallar el punto de intersección, V, entre la recta horizontal, R, y el plano anterior, Q
5 – Unir A y B con V y esta es una de las caras laterales de la pirámide.

---

Inicio > Sistema diédrico > Pirámides | |

Ejercicios de PIRÁMIDES en diédrico resueltos – 994

Inicio > Sistema diédrico > Pirámides

Dado un soporte compuesto por un tronco de pirámide recto con bases triangulares equiláteras, coronado en ambas bases por dos tetraedros de igual arista que las bases sobre las que se apoya. Conociendo tres puntos :
A (47, 83.5, 59.5) (alejamiento, cota, referencia)
B (72.5, 84.5, 115)
C (16.5, 33, 129.5)
Se pide:
a) Trazas del plano ABC.
b) Ángulo que forma dicho plano con los planos de proyección.
c) Lado de las bases mayor y menor del tronco de pirámide.
d) Proyecciones del tronco de pirámide.
e) Proyecciones de los dos tetraedros.
NOTA : D tiene mayor cota que A

---

SOLUCIÓN

Existen varias posibles formas de hacerlo. Comento una de ellas.
1 – Colocados los tres puntos A, B y C, se hace un cambio de plano para colocar el triángulo ABC en proyectante (línea de tierra segunda perpendicular a la dirección de la traza del plano que forma ABC), dando a’1b’1c’1

2 – Hacer otro cambio de plano para que el triángulo ABC esté en verdadera magnitud (tercera línea de tierra paralela a a’1b’1c’1, dando a1b1c1
3 – En el último cambio de plano se dibuja el cuarto vértice e1, del trapecio formado por ABCE
4 – En el último cambio de plano se hacen los abatimientos de las caras BCDF y ADEF, respecto de sus trazas c1b1 y a1e1, respectivamente. En realidad solo se dibujan las caras trapeciales en verdadera magnitud (líneas verdes relleno de rosa)
5 – Se desabaten los puntos (D) y (F) mediante perpendiculares a sus respectivas trazas b1c1 y a1e1, donde se corten ambas perpendiculares son las proyecciones de los puntos, d1 y e1
6 – Se determina la altura de esos puntos (líneas naranjas rellenas de azul)
7 – A partir de la proyección a’1b’1c’1, se llevan esa alturas (en perpendicular a esas proyecciones) y hasta la perpendicular a la tercera línea de tierra que pasa por d1 y e1
8 – Ya solo queda ir deshaciendo los cambios de plano

---

Inicio > Sistema diédrico > Pirámides | |

Inicio > Sistema diédrico > Pirámides

 

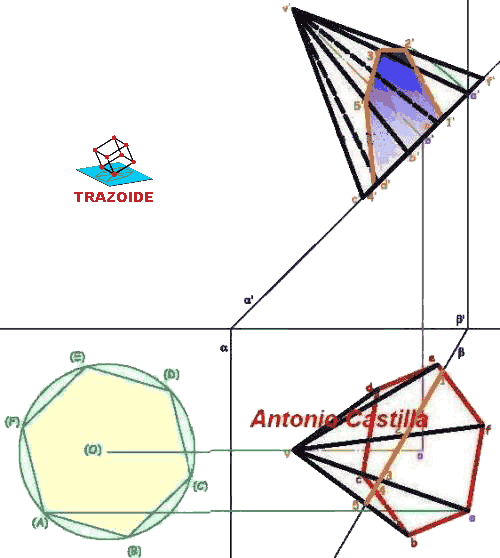
Hallar la altura de una pirámide regular de base un triángulo equilátero de lado 80 mm y ángulo diedro entre las caras laterales de 105º.

---

 

SOLUCIÓN

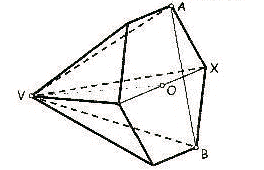
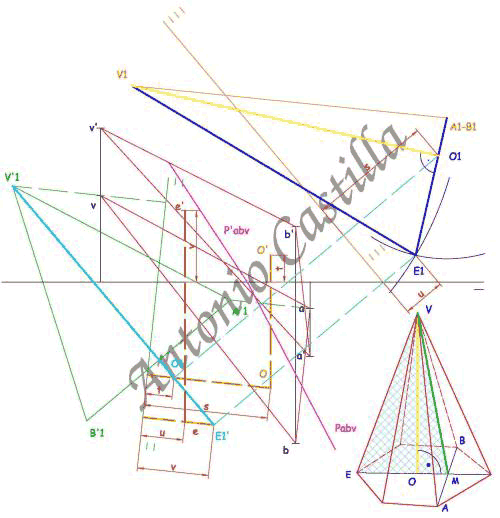
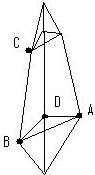
Supongamos la pirámide, ABCD, ya construida.

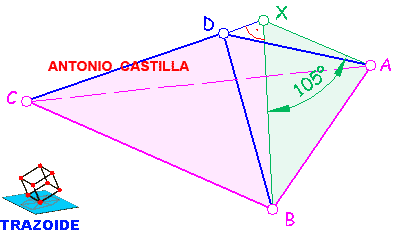
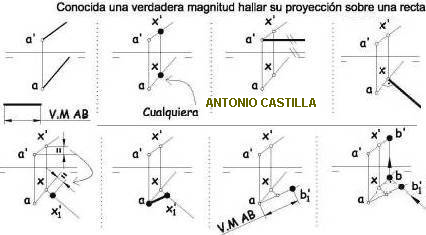
Para medir el ángulo diedro de dos caras laterales, CDB y CDA, trazaríamos dos perpendiculares a la arista común, CD, desde un punto de ella, X. El ángulo entre ambas perpendiculares es el ángulo diedro, 105º.

El punto por el que pasan las perpendiculares, X, puede ser cualquiera de la arista común, CD, pero también se puede tomar, de tal forma que, las perpendiculares pasen por los vértices, A y B, de la pirámide. De esta forma conocemos tres datos del triángulo ABX : es isósceles, el ángulo X = 105º y el lado AB = 80 mm.

Otro triángulo importante en el trazado es CBX (o CAX, son iguales). De este triángulo también conocemos tres elementos : es rectángulo (X = 90º), el lado CB = 80 mm y el lado BX que se obtendrá del triángulo ABX.

La realización práctica es la siguiente :

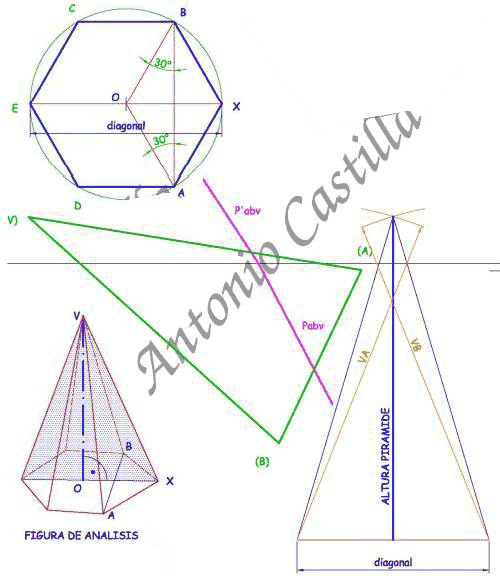
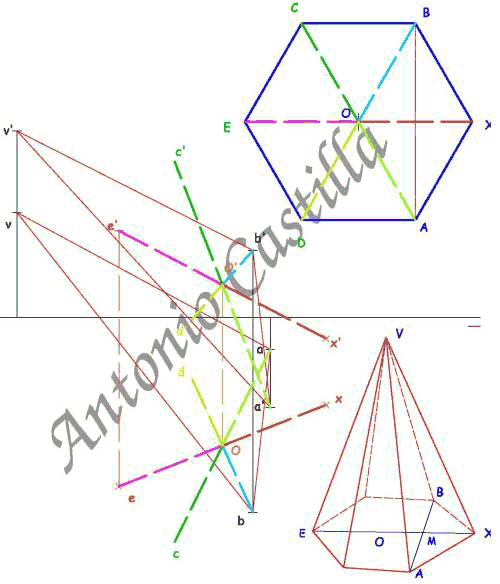
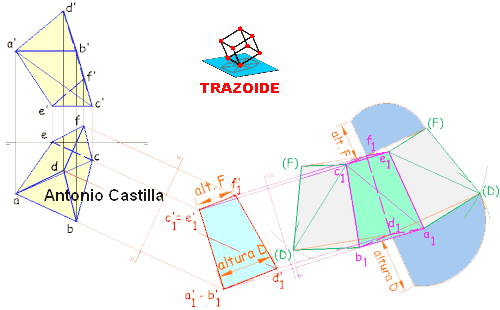
1 – En proyección horizontal se dibuja la base, ABC, como un triángulo equilátero de lado 80 mm, con uno de sus lados, AB, perpendicular al plano vertical de proyección (o a la línea de tierra).

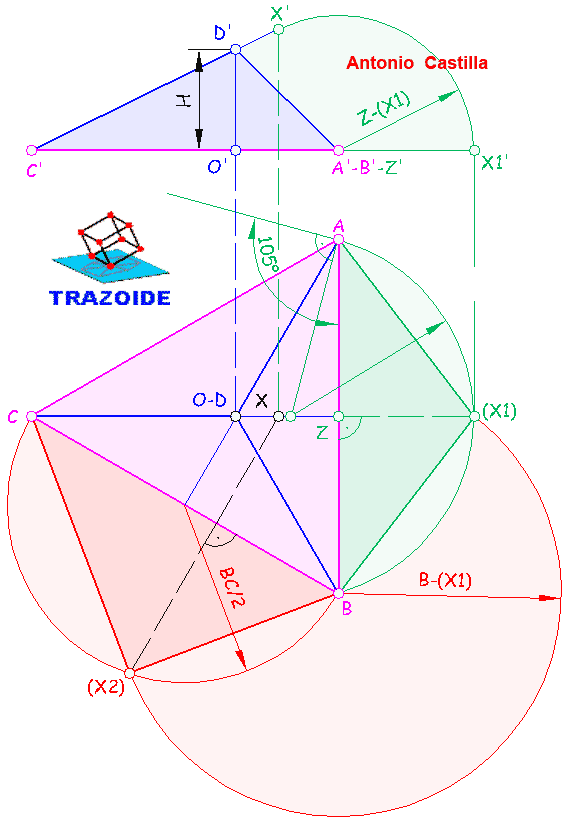
2 – El baricentro, O, del triángulo ABC se une con sus tres vértices, y con ello, tenemos la proyección horizontal completa de la pirámide, ABCD, buscada.

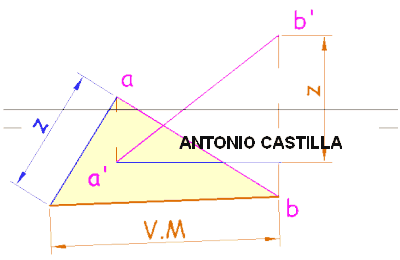
3 – Apoyándonos en el lado AB se dibuja un arco capaz de 105º y desde el centro de AB una perpendicular hasta cortar al arco. Este punto (X1) se une con A y B. El triángulo A-B-(X1) es el abatimiento del triángulo ABX alrededor de la traza AB. De esta forma hemos determinado la magnitud de AX o BX.

4 – A partir de BC se traza el arco capaz de 90º y se traza un arco con centro en B y radio la magnitud BX = B-(X1), obtenida del abatimiento anterior. Donde se corten, (X2), se une con B y C siendo el triángulo B-C-(X2) el abatimiento de BCX alrededor de BC.

5 – La proyección horizontal del punto X está en la perpendicular a su traza, AB, desde su abatimiento (X1). También estará en la perpendicular a la otra traza, BC, desde su abatimiento (X2). Donde se corten ambas, X, es su proyección horizontal.

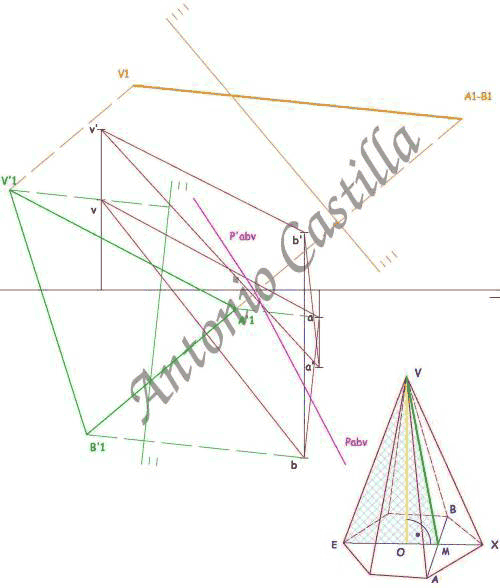
6 – Dibujamos la base, ABC, en proyección vertical. Esta es una paralela a la línea de tierra, A’B’C’.

7 – En proyección vertical la cara ABD y ABX se ven proyectantes. En concreto la cara ABX tiene de longitud la altura, Z-(X1), del triángulo abatido A-B-(X1). Así que con centro en Z’ y radio Z-(X1) se traza un arco.

8 – Desde la proyección horizontal de X se dibuja una perpendicular a la línea de tierra hasta cortar al arco anterior. El punto de corte es la proyección vertical X’.

9 – El punto X está en la arista CD, luego uniendo X’ con C’ tenemos la recta en la que se encuentra el cuarto vértice de la pirámide, D. Si desde la proyección horizontal de D se traza una perpendicular a la línea de tierra donde corte a C’-X’ es la proyección vertical D’.

10 – Unir las proyecciones verticales A’, B’ y C’ con D’ y tenemos la proyección vertical completa de la pirámide.

11 – Si en proyección vertical bajamos una perpendicular a la línea de tierra desde D’ hasta la base A’B’C’ se obtiene la altura de la pirámide, H = O’-D’.

 

---

 

Inicio > Sistema diédrico > Pirámides | |

 

Inicio > Sistema diédrico > Pirámides

 

Dados los puntos A y B que definen la altura de un tronco de pirámide recto de bases pentagonales regulares. La base mayor (punto B) mide 60 de lado y la base menor (punto A) mide 36 de lado. Los puntos C y D están en el punto medio de una arista, la base B tiene el punto D y la base A tiene el punto C. Se sabe que las aristas básicas que contienen a los puntos C y D son paralelas al plano horizontal de proyección.

Se pide :
a) Representar alzado y planta de las proyecciones de la base mayor.
b) Alzado y planta de la base menor.
c) Representar las aristas laterales que conforman el tronco de pirámide.
d) Determinar el ángulo que forman dos caras laterales contiguas.

Dato: Los puntos C y D tienen la mayor cota posible. Punto A (a = -10, c = -23, z = 54), B (a = 26, c = 39, z = 151). A y B son los centros de las bases y C y D son los puntos medios de las aristas laterales.

---

SOLUCIÓN

I – Por B dibujar un plano perpendicular a la recta AB.

II – Abatir el plano y el punto B.

III – En el abatimiento dibujar un pentágono de centro el punto B abatido y de lado 60 mm, colocándolo de tal forma que uno de sus lados sea paralelo a la traza horizontal del plano pero en la posición más alejada de esa traza de las dos posibles.

IV – Desabatir el pentágono.

V – Para la otra base seguir el mismo procedimiento.

VI – Unir los vértices de ambas bases.

 

---

 

Inicio > Sistema diédrico > Pirámides | |

 

PIRÁMIDES – 992

Ejercicios de PIRÁMIDES en diédrico resueltos – 991

Inicio > Sistema diédrico > Pirámides

Selectividad Andalucía
Dadas las proyecciones de las rectas R y S se pide :
1 – Hallar las trazas del plano P que contiene a las rectas R y S.
2 – Dibujar las proyecciones del hexágono regular que tiene dos de sus lados opuestos sobre las rectas R y S y uno de sus vértices sobre el plano horizontal de proyección, estando situado dicho polígono en el primer diedro de proyección.
3 – Determinar las proyecciones de la pirámide regular de base el hexágono obtenido, altura 70 mm, y situada en el primer diedro de proyección.

---

SOLUCIÓN

Dibujar el plano formado por las dos rectas y abatirlo junto con las rectas.
Para trazar el hexágono en el abatimiento :
1 – Abatir las dos rectas R y S
2 – A la mitad de la distancia que separa a R de S (en el abatimiento) se dibuja una paralela a R o S
3 – Donde esta paralela media corte a la traza horizontal del plano es el primer vértice, A, del hexágono
4 – Desde ese punto, A, levanta líneas que formen 30º con la paralela media, hacia ambos lados. Estas líneas cortarán a R y S en dos puntos que son dos vértices del hexágono, B y F, siendo además A-B o A-F el valor del lado del hexágono en verdadera magnitud.
5 – Sobre R y S, y a partir de B y F llevar una longitud igual a A-B o A-F, consiguiendo dos nuevos vértices, C y E
6 – Con centro en C y E y radio A-B o A-F hacer dos arcos. Donde se corten es el último vértice, D, que deberá estar sobre la paralela media

---

Inicio > Sistema diédrico > Pirámides | |

Ejercicios de PIRÁMIDES en diédrico resueltos – 990

Inicio > Sistema diédrico > Pirámides

De un hexágono regular ABCDEF de 5 cm de lado se sabe que el lado AB está en el plano horizontal de proyección y sobre la recta que pasa por K (-5, 0, 0) (referencia, alejamiento, cota) y forma 30º con la línea de tierra. El lado EF está sobre el plano vertical de proyección.
Se pide:

– Dibujar el hexágono.
– Dibujar la pirámide regular que lo tiene por base sabiendo que esta tiene una cara lateral apoyada en el plano horizontal de proyección. Señalar la parte de la pirámide que queda en el primer cuadrante.

---

SOLUCIÓN

Primera parte. Obtención de la base hexagonal.

1 – Colocar el punto K y desde él trazar una recta que forme 30º con la línea de tierra. Esta es la traza horizontal del plano que contiene al hexágono, p.

2 – Dibujar un hexágono, a1-b1-c1-d1-e1-f1, de lado 50 apoyado en la recta anterior y en cualquier lugar.
3 – Por K trazar una paralela a e1-f1. Esta es la traza vertical del plano abatida, (p’).
4 – Por f1 hacer una paralela a p y donde corte a (p’) es el vértice (F) del hexágono abatido buscado.
5 – Trazar el resto del hexágono abatido, (A)-(B)-(C)-(D)-(E)-(F), por paralelas al primero, a1-b1-c1-d1-e1-f1.
6 – Las proyecciones horizontales de A y B coinciden con sus abatimientos y las verticales están sobre la línea de tierra.
7 – Por (E) y (F) trazar perpendiculares a la traza horizontal del plano, p, y donde corten a la línea de tierra son sus proyecciones horizontales. Para las verticales subir perpendiculares a la línea de tierra y con centro en K y radios hasta los puntos abatidos, (E) y (F), trazar sendos arcos. Donde corten a las verticales son las proyecciones verticales.
8 – Unir las proyecciones de los puntos, B con A, A con F y F con E.
9 – El lado E-D es paralelo al lado A-B y de igual longitud. Por el extremo D una paralela al lado A-F y con su misma longitud se obtiene C. Unir C con B.

Segunda parte. Obtención del vértice de la pirámide.

10 – Por el centro de la base hacer perpendiculares a las trazas del plano.

11 – Hallar la traza horizontal de ese eje y ese es el vértice de la pirámide. Unirlo con los puntos de la base.

---

Inicio > Sistema diédrico > Pirámides | |