Mes: octubre 2014

Ejercicios de paralelismo – 992

Inicio > Sistema diédrico > Paralelismo en diédrico

Forma de una recta paralela al primer bisector

---

SOLUCIÓN

Existen tres tipos :

Recta general, R. Sus proyecciones forman el mismo ángulo respecto de la línea de tierra y hacia el mismo lado, y no se cortan en el mismo punto de la línea de tierra. En el perfil forman 45º con el plano horizontal de proyección, abierto hacia la derecha (o paralela al primer bisector).

Recta paralela a la línea de tierra, S. Sus proyecciones tendrán una distancia distinta respecto de la línea de tierra.

Recta de perfil, T. En el perfil formará 45º con el plano horizontal de proyección, abierto hacia la derecha (o paralela al primer bisector)

---

Inicio > Sistema diédrico > Paralelismo en diédrico | | Vídeos sobre paralelismo

Ejercicios de octaedros resueltos – 999

Inicio > Sistema diédrico > Octaedros

Determinar las proyecciones de un octaedro regular del que conocemos las condiciones de su cara inferior :
– Un vértice se encuentra en el plano P(-5, 4, 6) y en el primer bisector, a cota 40 mm
– El lado opuesto a dicho vértice se encuentra por encima del plano P, en uno paralelo, a la distancia la altura de la cara, y en una recta que forma 45° con la recta intersección del plano P con el primer bisector
– Arista del octaedro 80 cm.

---

SOLUCIÓN

1 – Dibujar el plano P

2 – Situar el punto A que está en el primer bisector y en el plano P
3 – Aparte, construir un triángulo equilátero con el lado dado. Determinar el valor de la altura de ese triángulo
4 – Desde el vértice A trazar una perpendicular al plano P y sobre ella llevar la proyección de la altura del triángulo, h. Su extremo es el punto M, que será el punto medio del lado opuesto al vértice A. La proyección de la altura, h, la he determinado con un cambio de plano, a1′-m1′
5 – Hallar la intersección, I, del plano P con el primer bisector
6 – Abatir la recta intersección y el vértice A respecto del plano P
7 – En el abatimiento dibujar una recta (A)-(X) que forme 45° respecto de la intersección (I)
8 – Sobre esa recta llevar en verdadera magnitud la mitad de la longitud del lado del octaedro, L/2. Su extremo es (X)
9 – Desabatir (X) y unirlo con el punto A
10 – Dibujar una paralela a las proyecciones de A-X por las proyecciones del punto M. Obteniéndose las proyecciones del segundo vértice B
11 – Llevar hacia el otro lado de M las proyecciones de M-B. Este nuevo punto, C, es el tercer vértice del triángulo buscado

---

Inicio > Sistema diédrico > Octaedros | |

Ejercicios de octaedros resueltos – 998

Inicio > Sistema diédrico > Octaedros

Octaedro conocido un vértice B y que una diagonal, AF, está sobre la recta R

---

SOLUCIÓN

1 – Formar un plano, P, con la recta R y el punto B

2 – Abatir la recta R y el punto B
3 – En el abatimiento hacer una perpendicular a la recta (R) desde el punto (B), esto nos da la medida de la mitad de la diagonal
4 – Dibujar, en el abatimiento, un cuadrado de centro, (O), en el punto de corte de la perpendicular con la recta (R) y de semidiagonal (O)-(B). Estos son cuatro de los vértices abatidos del octaedro, (A)-(B)-(F)-(D)
5 – Desabatir esos cuatro puntos
6 – Desde el centro del cuadrado, O, en proyección horizontal y vertical, levantar perpendiculares a las trazas del plano, y determinar sobre ellas la proyección de la semidiagonal calculada en el abatimiento.
7 – Esta proyección llevada hacia ambos lados del centro nos da los dos vértices restantes, C y E

---

Inicio > Sistema diédrico > Octaedros | |

Inicio > Sistema diédrico > Octaedros

 

Dibujar las proyecciones de alzado y planta de un octaedro, en su correcta visibilidad, que tiene una cara apoyada en un plano que pasa por el punto A(230, 35, 45) y que forma 45º con el plano horizontal y 60º con el vertical.
El punto A es el vértice de mayor alejamiento de dicha cara y la arista opuesta de dicha cara forma 45º con el plano horizontal de proyección y dista 50 mm del vértice A.

---

SOLUCIÓN

1 – Construir el plano, P,con los ángulos dados (45º con PH y 60º con PV).

2 – Abatir el plano y el vértice A.

3 – El lado, BC, de la cara opuesto al vértice A forma 45º con el plano horizontal, lo mismo que el plano al que pertenece. Luego dicha recta será la recta de máxima pendiente, es decir, es perpendicular a la traza horizontal del plano. Por ello, hacer una paralela, (A)-(M), a la traza horizontal del plano, en el abatimiento, pasando por el punto A abatido y sobre ella medir 50 mm.

4 – Ese punto, (M), es el punto medio del lado buscado. Dibujar por él una recta perpendicular, (B)-(C), a la traza horizontal del plano y desde el vértice A abatido hacer dos rectas, (A)-(B) y (A)-(C), que formen 30º respecto de la paralela, (A)-(M), a la traza horizontal del plano que pasa por A.

5 – Donde corte a la perpendicular, (B) y (C), son los otros dos vértices del triángulo.

6 – Desabatir el triángulo y esa es la cara del octaedro.

 

---

 

Inicio > Sistema diédrico > Octaedros | |

 

octaedros – 997

Ejercicios de octaedros resueltos – 996

Inicio > Sistema diédrico > Octaedros

Determinación de la altura de cuerpo (o principal), H, de un octaedro conocido el valor del lado, L

---

SOLUCIÓN

19 – Se dibuja un triángulo equilátero con el valor de la arista, L, del octaedro en verdadera magnitud

20 – La altura de ese triángulo, h, es el valor de la altura de cara del octaedro
21 – Se dibuja la sección principal del octaedro (un rombo con lado la altura de cara del octaedro), o bien solo media (un triángulo isósceles con dos lados formados con la longitud de la altura de cara, h, y el tercero con la longitud del lado, L, del octaedro)

22 – Se traza la altura de la sección principal, H, o bien, la altura de la semisección principal desde el vértice donde se une la longitud del lado, L, con el de la altura de cara, h. Esta perpendicular es el valor de a altura del octaedro, H

---

Inicio > Sistema diédrico > Octaedros | |

Ejercicios de octaedros resueltos – 995

Inicio > Sistema diédrico > Octaedros

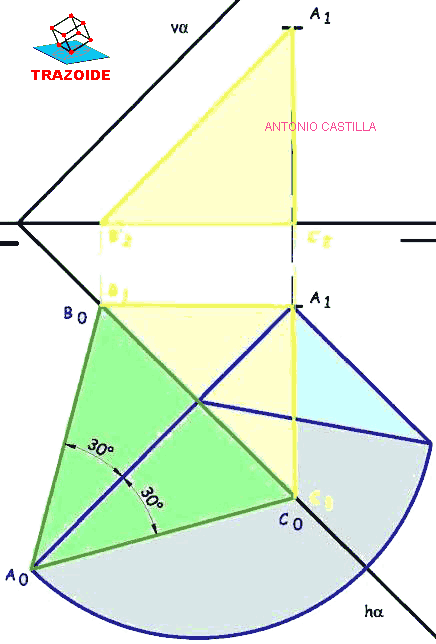
Dibujar un octaedro regular, 1-2-3-4-5-6, si :
– Una diagonal, 1-6, es perpendicular al plano Q que pasa por la línea de tierra y forma 30º con el plano horizontal de proyección.
– Un vértice es 1(0, 5, 2’5). Las coordenadas están en centímetros y son referencia, alejamiento y cota.
– Los vértices 2 y 6 están en el plano vertical de proyección.

---

SOLUCIÓN

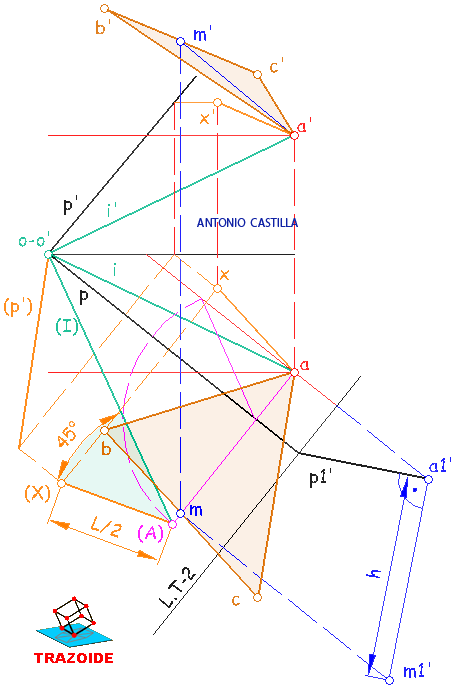
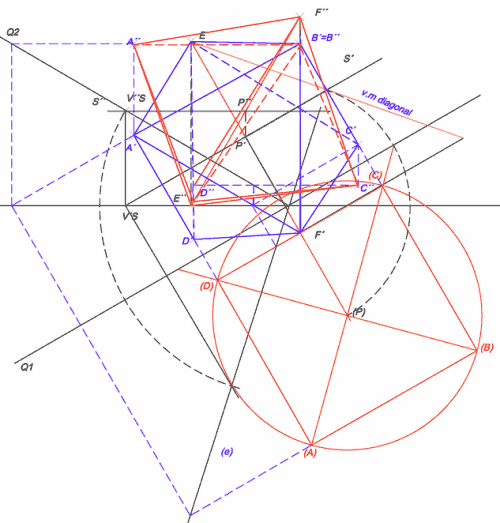
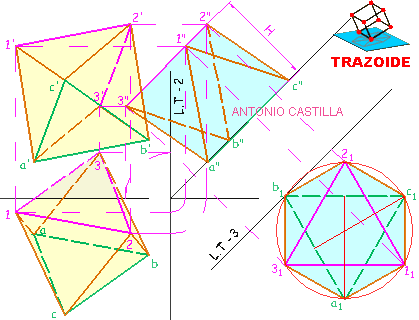
1 – Dibujar las tres proyecciones del punto 1 y el plano Q que pasa por línea de tierra en el perfil formando 30º con el plano horizontal de proyección.

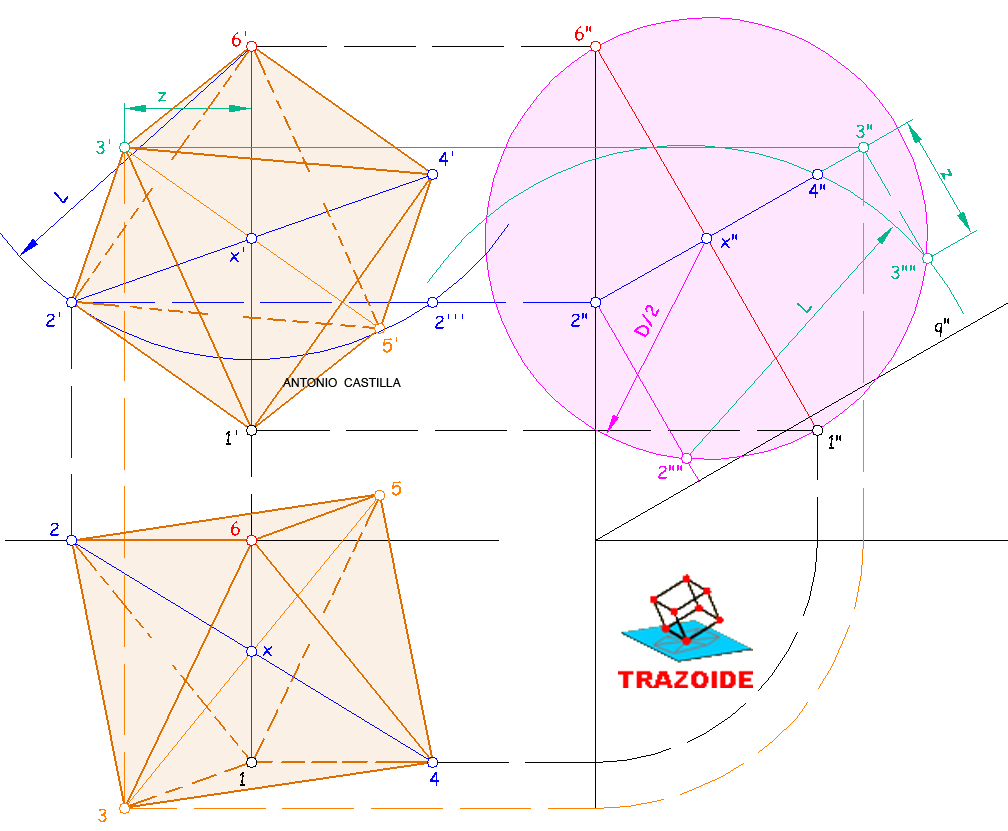
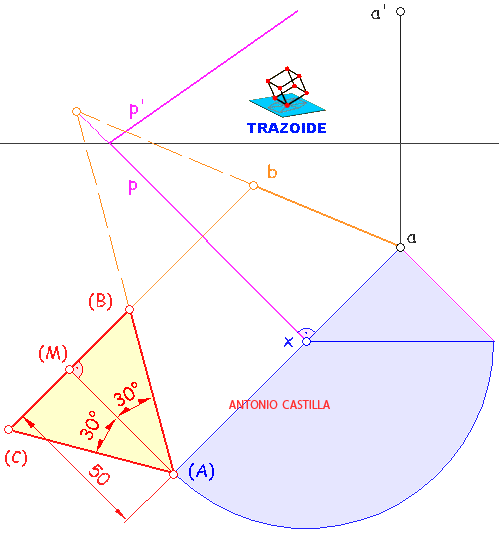
2 – En el perfil, desde el punto 1" se traza una perpendicular al plano Q hasta cortar al plano vertical de proyección. El punto de corte es el vértice opuesto 6". Determinar las otras proyecciones, 6 y 6′, con la misma referencia que el punto 1.
3 – La distancia entre las proyecciones 1" y 6" del perfil es la verdadera magnitud de la diagonal del octaedro. Aparte situar la medida de la diagonal, D, y levantar por sus extremos líneas que formen 45º con ella hasta cortarse. Estos segmentos nos dan la longitud de la arista, L, del octaedro.
4 – En el perfil, dibujar una perpendicular a la diagonal 1"-6" por su punto medio, x", hasta cortar al plano vertical de proyección. Este punto es el vértice 2".
5 – Desde la proyección de perfil 2" hacer una paralela a la línea de tierra hacia la proyección vertical. Con centro en la proyección vertical del punto 6′ y radio la verdadera magnitud de la arista del octaedro, L, hacer un arco. El arco corta a la paralela a la línea de tierra en dos puntos, 2′ y 2»’, que son las dos posibles soluciones para la proyección vertical del punto 2. Trabajaré con 2′. Su proyección horizontal está sobre la línea de tierra.
6 – El vértice 4 opuesto a 2 se obtiene uniendo las proyecciones de 2 con el punto medio, X, de la diagonal 1-6 y llevando las mismas distancias que hay en proyección entre 2-X hacia el otro lado de X.
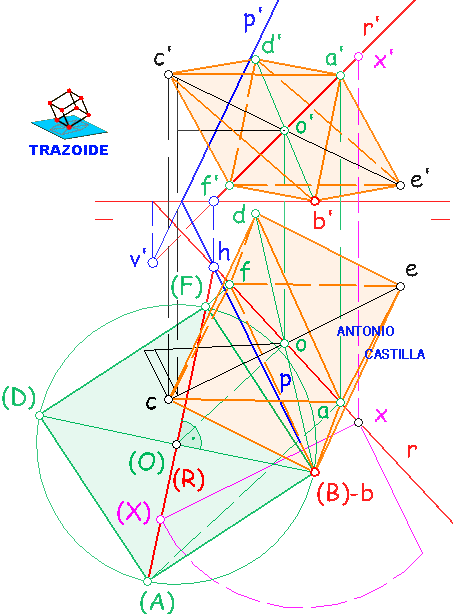
7 – En el perfil con centro en el punto medio de la diagonal, x", y radio la mitad de la diagonal del octaedro, D/2, se traza un arco.
8 – Desde la proyección de perfil 2" se dibuja una perpendicular al plano Q hasta el arco. El punto de corte, 2"", es el vértice del plano de simetría (cuadrado) en una sección rebatida.
9 – Con centro en ese punto 2"" y radio la longitud de la arista del octaedro, L, se dibuja un nuevo arco que cortará al anterior en el vértice 3"" de la sección rebatida.
10 – Se dibuja una perpendicular al plano Q por 3"" hasta una paralela al plano Q por el punto medio, x", de la diagonal 1"-6". Esto nos la proyección de perfil 3".
11 – Hacer una paralela a la línea de tierra por 3" y medir la distancia, Z, entre las proyecciones 3" y 3"".
12 – Llevar esa distancia, Z, desde la proyección vertical de la diagonal 1′-6′ sobre la paralela a la línea de tierra que se hizo por 3". Esto nos da la proyección vertical 3′.
13 – Con la proyección de perfil 3" y la proyección vertical 3′ se determina la proyección horizontal 3.
14 – Uniendo las proyecciones del punto 3 con el punto medio X y llevando la misma distancia hacia el otro lado se determina el vértice opuesto 5.
15 – Unir los seis vértices.

---

Inicio > Sistema diédrico > Octaedros | |

Ejercicios de octaedros resueltos – 994

Inicio > Sistema diédrico > Octaedros

Determinación de la altura de cara y de cuerpo (o principal) de un octaedro conocida su arista.

---

SOLUCIÓN

Altura de cara de un octaedro.

a – Construir un triángulo equilátero con el valor de la arista, L
b – La altura de ese triángulo, h, es el valor de la altura de la cara del octaedro

Altura de cuerpo (o principal).

c – Construir un triángulo isósceles con el valor del lado del octaedro, L, y el de la altura de cara, h, siendo la altura de cara, h, la que se repite en el triángulo
d – Dibujar la altura de ese triángulo respecto del lado formado con la longitud h
e – Esa nueva altura, H, es el valor de la altura del octaedro

---

Inicio > Sistema diédrico > Octaedros | |

Ejercicios de octaedros resueltos – 993

Inicio > Sistema diédrico > Octaedros

Un octaedro cuyo vértice de mayor cota es F (7, 7, 1) tiene su sección cuadrada máxima ABCD en un plano perpendicular al primer bisector que forma 30 grados con la línea de tierra, sabiendo que AB es horizontal, y su vértice E de menor cota está en H.
Determinarlo y cortarlo por un plano de perfil que pasa por su centro geométrico (representar el corte de perfil).

---

SOLUCIÓN

La sección máxima cuadrada de un octaedro la forman cuatro vértices cualquiera. En el gráfico la línea roja :

A esa sección máxima también se la llama otra veces plano de simetría.
Ese cuadrado es siempre perpendicular a la diagonal del octaedro (en azul), la cual pasa por su centro.

El proceso sería este :
1 – Desde el punto F se traza una recta que forme 60º con la línea de tierra.
2 – Se halla la traza horizontal de esa recta, que será el punto E, y por tanto ya se tiene la diagonal del cuerpo, FE.
3 – Por el punto medio de FE se hace un plano perpendicular o uno que sea perpendicular al primer bisector y forme 30º sus trazas con la línea de tierra, lo mismo es.
4 – Se abate el plano y el punto medio de FE.
5 – En el abatimiento se dibuja el cuadrado ABCD con centro en el punto medio de FE, cuya diagonal sea igual a la verdadera magnitud de FE y que formen (sus diagonales) 45º con respecto a la traza horizontal del plano.
6 – Desabatir el cuadrado y unir sus vértices con E y F.

---

Inicio > Sistema diédrico > Octaedros | |

Ejercicios de octaedros resueltos – 992

Inicio > Sistema diédrico > Octaedros

Dibujar, en el primer diedro, las proyecciones de un triángulo equilátero ABC situado en el primer plano bisector, siendo A(120, 25, ?) y B(200, 40, ?).
Construir un octaedro conocida una cara, ABC, apoyada en el primer plano bisector.

---

SOLUCIÓN

23 – En el cambio de plano (L.T – 3) se dibuja un triángulo igual al obtenido, a1-b1-c1, pero girado 180º, 1sub1-2sub1-3sub1. Uniéndose los vértices contiguos de los dos triángulos. Todo esto forma la proyección completa del octaedro en el último cambio de plano.

24 – En el perfil (L.T – 2) se dibuja una paralela al primer bisector separada de este una distancia igual a la de la altura de cuerpo del octaedro, H
25 – Se lleva sobre esa paralela los puntos del segundo triángulo, dando 1"-2"-3"
26 – Se unen, en el perfil, los puntos de las dos bases, a"-b"-c" y 1"-2"-3", entre sí siguiendo el mismo orden en el que están unidos en el hexágono que se forma en el último cambio de plano, es decir, A-1-C-2-B-3-A
27 – Se obtienen las proyecciones verticales del segundo triángulo deshaciendo el cambio de plano, 1′-2′-3′
28 – Se unen las dos bases, a’-b’-c’ y 1′-2′-3′, de las proyecciones verticales siguiendo el mismo orden del hexágono, A-1-C-2-B-3-A
29 – Se determinan las proyecciones horizontales del segundo triángulo, a-b-c, deshaciendo el perfil y con la misma referencia que sus proyecciones verticales
30 – Se unen las dos bases, a-b-c y 1-2-3, de las proyecciones horizontales siguiendo el mismo orden del hexágono, A-1-C-2-B-3-A

Por supuesto, también se puede proyectar la segunda base en el abatimiento y después contraproyectar.

---

Inicio > Sistema diédrico > Octaedros | |

Ejercicios de octaedros resueltos – 991

Inicio > Sistema diédrico > Octaedros

El punto A es un vértice de un octaedro que tiene tres aristas contenidas en el plano P, estando también una de ellas contenida en el plano horizontal de proyección.
Dibujar las proyecciones de la figura.

---

SOLUCIÓN

Cuando el enunciado dice " tiene tres aristas contenidas en el plano " significa que una cara (3 aristas) está sobre el plano.
Normalmente cuando se tiene una cara sobre un plano este se abate y en el abatimiento se dibuja dicha cara en verdadera magnitud y forma.
También dice, " una de ellas contenida en el plano horizontal de proyección. " significa que esa arista tendrá su proyección horizontal sobre la traza horizontal del plano y la vertical sobre la línea de tierra.
El punto dado, A, no pertenece a esa arista, ya que si así fuese estaría sobre la traza horizontal del plano, por lo tanto es el vértice opuesto de esa arista.
Una vez aclarado estos detalles, pasamos a resolverlo (los colores que indico hacen referencia a mi dibujo) :
1 – Se abate el punto dado, A (en color azul).

2 – En el abatimiento la cara del octaedro contenida en el plano dado estará en verdadera magnitud, siendo un vértice el punto A0, y los otros dos estarán sobre la traza horizontal del plano (h alfa). Por lo que se hará un triángulo equilátero a partir del punto A0, mediante dos rectas que formen 30º respecto de la perpendicular a la traza del plano (en color verde), obteniéndose B0 y Co.
3 – El desabatimiento de esos puntos coincide sus abatimientos por estar sobre la traza alrededor de la que se abate. Y uniéndolos con A1 se obtiene la proyección horizontal de la cara (en amarillo).
4 – Basta con subirlos a la línea de tierra para determinar sus proyecciones verticales, B2 y C2, que unidos con A2 da la proyección vertical (en amarillo).

---

Inicio > Sistema diédrico > Octaedros | |