Mes: octubre 2014

Ejercicios de octaedros resueltos – 990

Inicio > Sistema diédrico > Octaedros

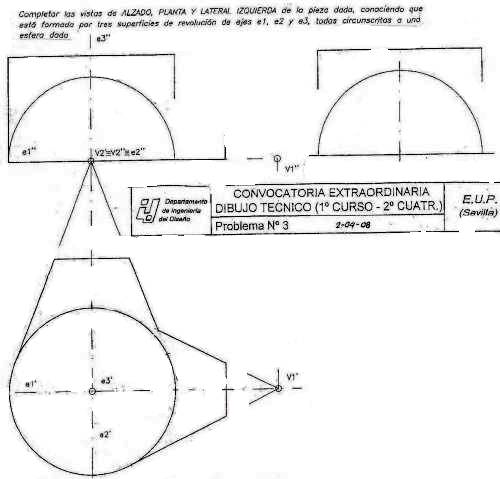
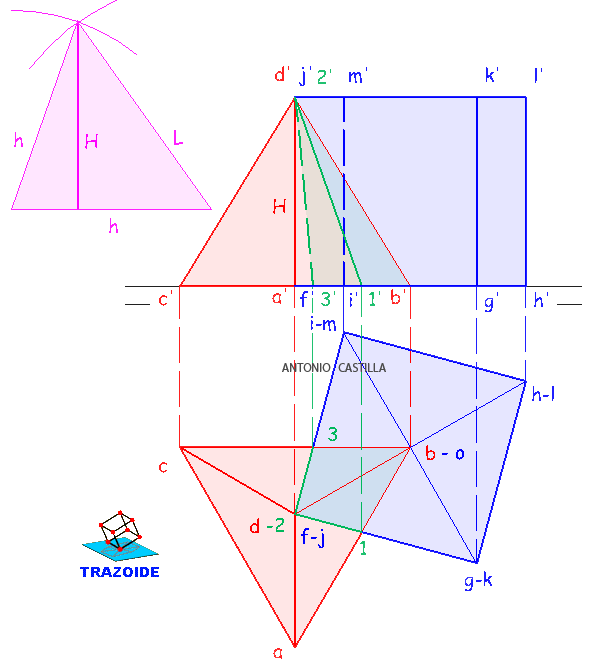
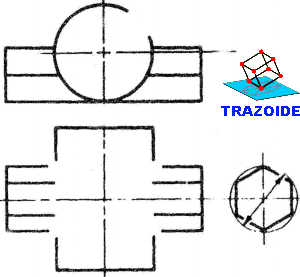
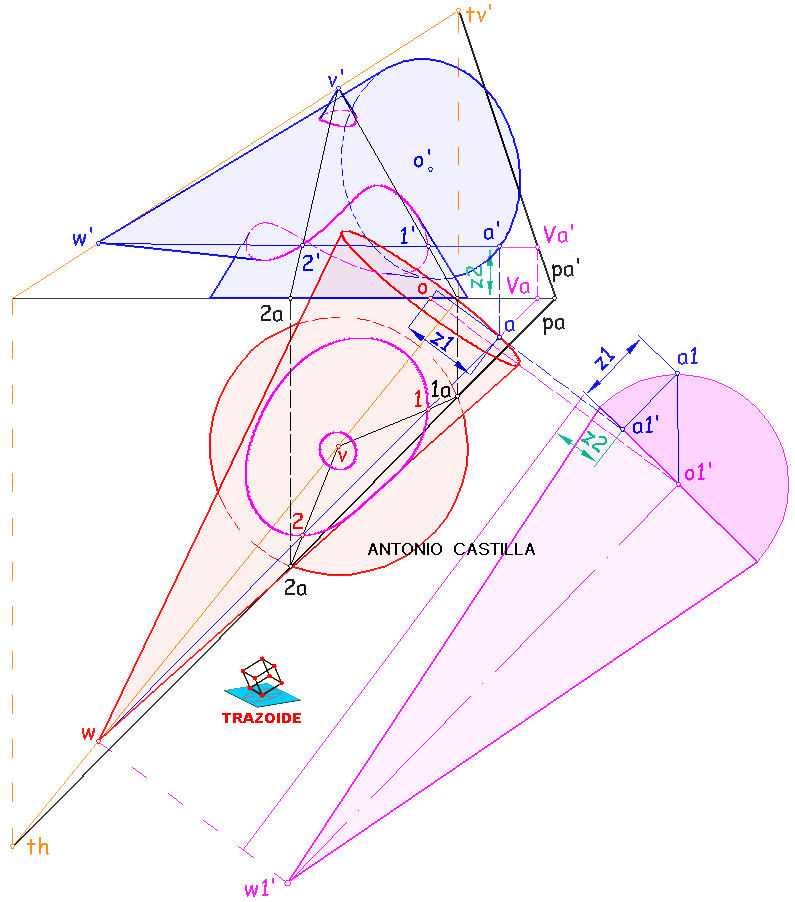
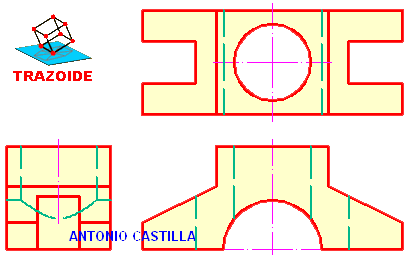
Un octaedro de lado 4 está apoyado por su cara ABC en un plano perpendicular al primer bisector, cuya referencia es -5. A es (3, 3, 0) y AB es horizontal, siendo C de cota máxima. Representarlo.

---

SOLUCIÓN

Son varios mini-problemas :

Construir un plano perpendicular al primer bisector, cuya referencia es -5, y pasa por A(3, 3, 0)

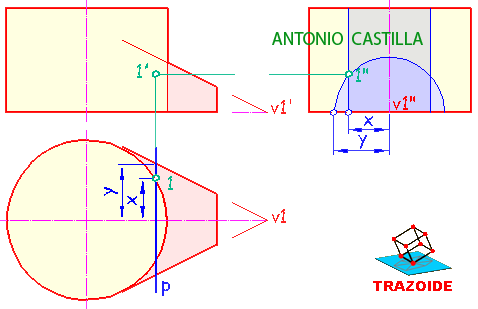
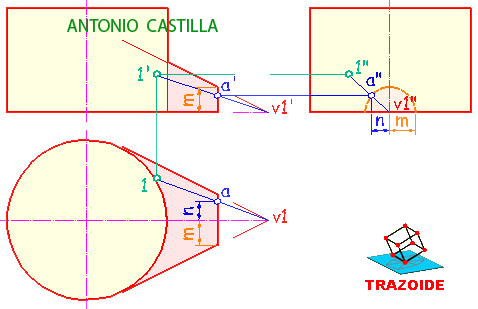
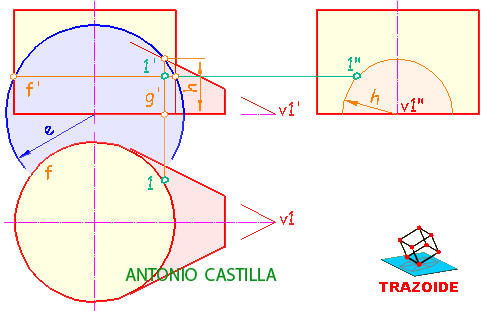
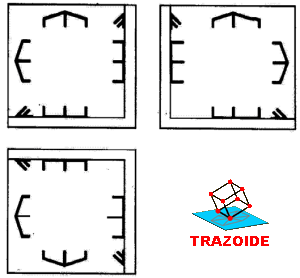
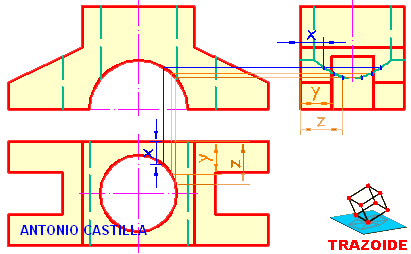
1 – Llevas el punto A al perfil.
2 – Haces, en el perfil, una recta perpendicular al primer bisector pasando por el punto A.
3 – Hallas, en el perfil, las trazas de esa recta.
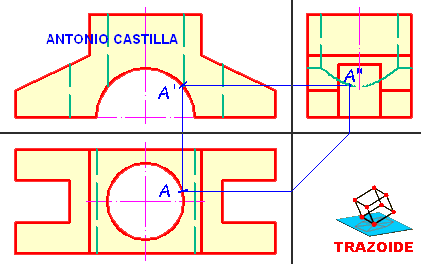
4 – Dibujas la recta, en las proyecciones principales, pasando por A y perpendiculares a la línea de tierra.
5 – Llevas las trazas halladas en el perfil a esas proyecciones.
6 – Unes el vértice del plano con esas trazas y tienes las trazas del plano.
A continuación es necesario conocer algunas magnitudes del octaedro.

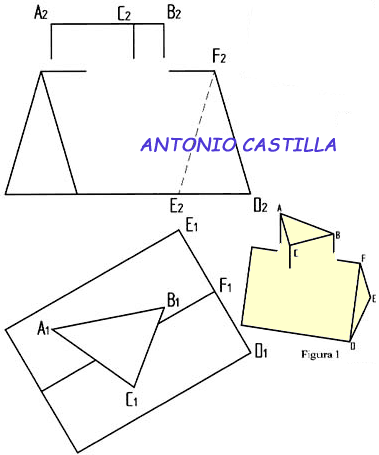
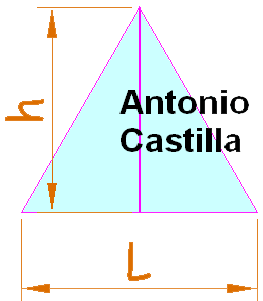
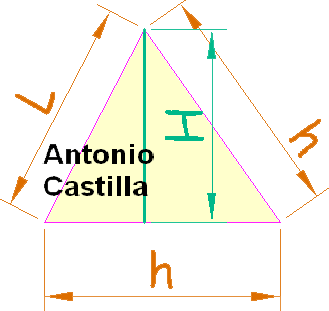
Determinación de la altura de cara de un octaedro conocida su arista

a – Construir un triángulo equilátero con el valor de la arista, L.
b – La altura de ese triángulo, h, es el valor de la altura de la cara del octaedro.

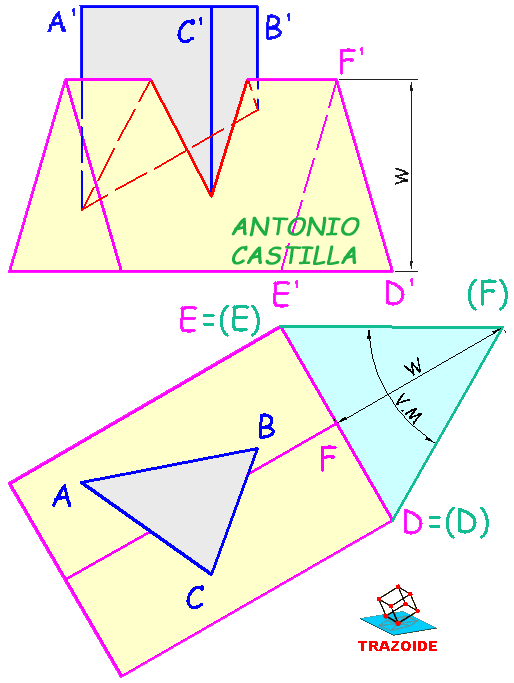
Determinación de la altura de cuerpo (o principal) de un octaedro

c – Construir un triángulo isósceles con el valor del lado del octaedro, L, y el de la altura de cara, h, siendo la altura de cara, h, la que se repite en el triángulo.
d – Dibujar la altura de ese triángulo respecto del lado formado con la longitud h.
e – Esa nueva altura, H, es el valor de la altura del octaedro.

Por último, el problema principal :

Dibujar un octaedro de lado 4, apoyado por su cara ABC en un plano perpendicular al primer bisector, cuya referencia es -5. A es (3, 3, 0) y AB es horizontal, siendo C de cota máxima.

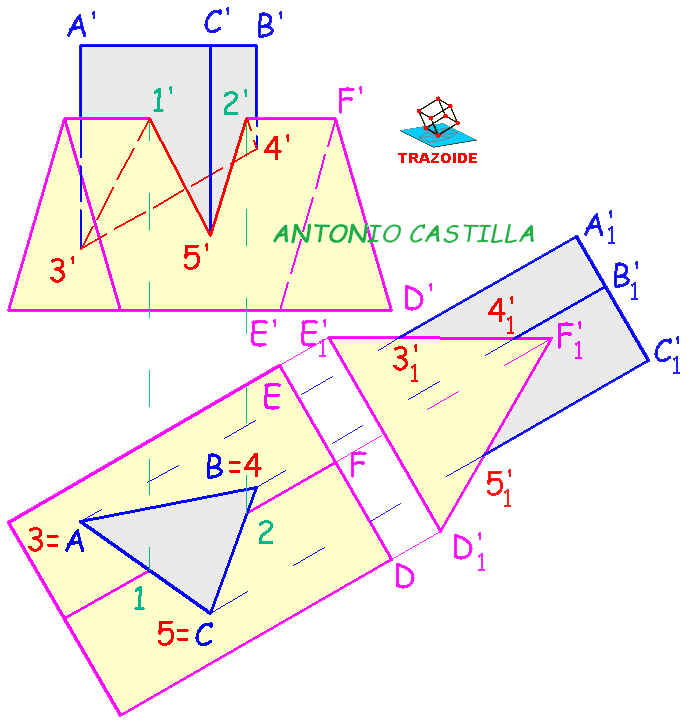
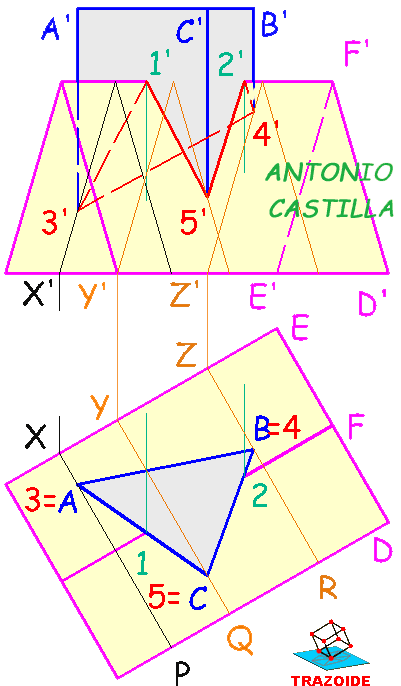
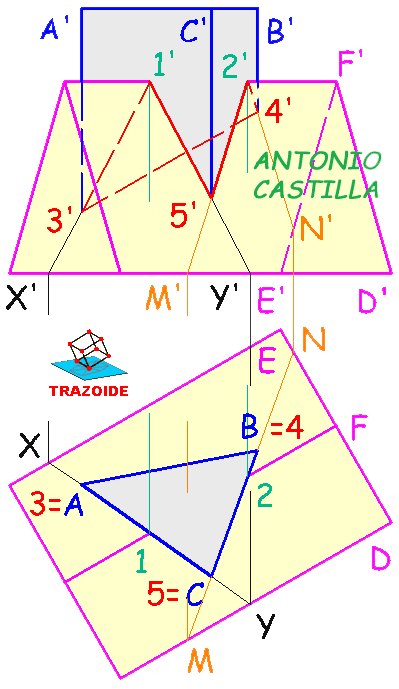
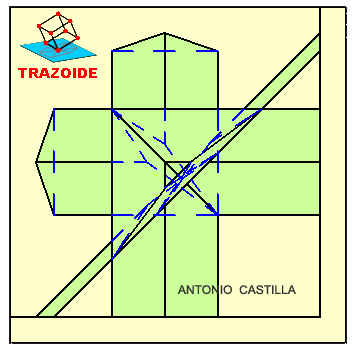
I – Abatir el plano y el punto A.
II – Por A dibujar una recta paralela a la traza horizontal del plano y sobre ella medir la longitud del lado, 4. Esto da el vértice B.
III – En el abatimiento, trazar un triángulo equilátero ABC, eligiendo de las dos posiciones posibles para C la que está más alejada de la traza horizontal del plano.
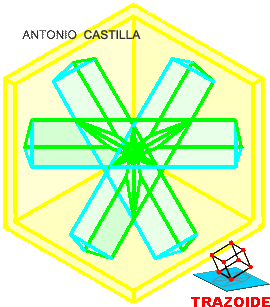
IV – Dibujar un segundo triángulo, al que llamaré 1-2-3, con el mismo centro que el primero pero girado 180º. Esto formará un polígono estrellado de seis vértices (estrella de David).
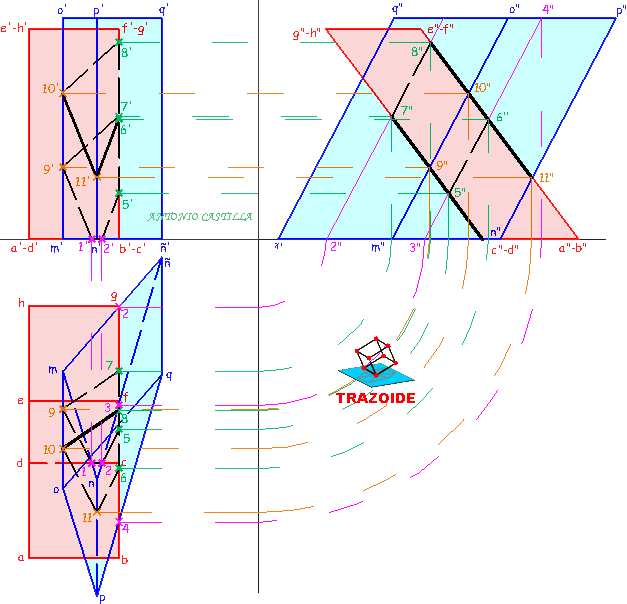
V – Desabatir los dos triángulos.
VI – Levantar el triángulo 1-2-3 una distancia igual a la de la altura principal del octaedro.
VII – Unir los vértices de ambos triángulos formando el resto de las caras del octaedro.

---

Inicio > Sistema diédrico > Octaedros | |

Ejercicios de intersecciones de cuerpos – 999

Inicio > Sistema diédrico > Intersecciones de cuerpos en diédrico

Completar las vistas de alzado, planta y lateral izquierda de la pieza dada conociendo que está formada por tres superficies de revolución de ejes e1, e2 y e3, todos circunscritos a una esfera dada.

---

SOLUCIÓN

INTERSECCIÓN DE UN CILINDRO RECTO CON UN cono recto mediante planos

1 – Trazar un plano de perfil, P

2 – El punto de corte, 1, con el cilindro en la proyección horizontal es un punto de la curva intersección
3 – Para llevar el punto al perfil, tomar la medida X y dibujar sendas generatrices en el perfil. Con la medida Y se dibuja, en el perfil, la circunferencia sección que produce el plano en el cono
4 – Donde las generatrices corten a ala circunferencia es el punto, 1", llevado al perfil
5 – Para determinar su proyección vertical, 1′, basta con levantar una perpendicular a la línea de tierra desde la proyección horizontal, 1, y una horizontal desde su proyección de perfil, 1". Donde ambas se encuentren es la proyección vertical del punto, 1′
6 – Trazar varios planos más y repetir el proceso para obtener más puntos

INTERSECCIÓN DE UN CILINDRO RECTO CON UN CONO RECTO mediante generatrices

7 – Dibujar en el perfil una sección recta (base) con la medida M de radio, tomada en el alzado o en la planta

8 – Trazar una división, a", en la sección recta, en el perfil
9 – Unirla con el vértice del cono, v1", y se obtiene una generatriz
10 – Para llevar la generatriz a la proyección horizontal tomar la medida N del perfil y llevarla a la planta. Uniendo la proyección horizontal del punto, a, con el vértice del cono, v1, se determina la generatriz
11 – Llevar la división, a", a la proyección vertical con una horizontal. Unir a’ con v1′
12 – En la proyección horizontal se obtiene el punto de intersección, 1, de la generatriz a-v1 con el cilindro
13 – Llevarlo a a’-v1′ mediante una perpendicular a la línea de tierra, 1′
14 – Con una nueva horizontal se lleva a a"-v1" dando su perfil 1"
15 – Repetir todo el proceso con otras divisiones

INTERSECCIÓN DE UN CILINDRO RECTO CON UN CONO RECTO mediante esferas

16 – Dibujar, en proyección vertical, una esfera de radio E con centro en el punto de corte del eje del cilindro y el cono

17 – Determinar la intersección de la esfera con el cilindro, uniendo donde se corten la esfera con el cilindro, f’ (circunferencia que se ve de canto)
18 – Determinar la intersección de la esfera con el cono, uniendo donde se corten, g’ (circunferencia que se ve de perfil)
19 – Donde se corten ambas es un punto de la curva intersección, 1′
20 – Para su proyección horizontal, 1, bajar una vertical hasta cortar al cilindro
21 – Tomar la medida del radio, H, en la proyección vertical, que produce la esfera en el cono y con ella dibujar la sección en el perfil
22 – Mediante una horizontal se obtiene sobre esa sección la proyección de perfil del punto, 1"
23 – Repetir con otras esferas de distinto radio

---

Inicio > Sistema diédrico > Intersecciones de cuerpos en diédrico | |

Ejercicios de intersecciones de cuerpos – 997

Inicio > Sistema diédrico > Intersecciones de cuerpos en diédrico

Examen del pais vasco del año 2006 junio.

En la figura 1 se representan, incompletos, un tejado a dos aguas y una chimenea.
El tejado tiene dos faldones con igual pendiente respecto al suelo horizontal. La chimenea es prismática, de base superior triangular ABC y aristas laterales verticales. Se pide, prolongando hacia abajo sus aristas verticales, determinar, en las vistas de alzado y planta dadas, la intersección de las caras laterales de la chimenea con los faldones del tejado. Visualizar el resultado, distinguiendo entre aristas vistas y ocultas. Determinar también el ángulo diedro formado por los faldones.

---

SOLUCIÓN

El problema se puede resolver de varias maneras :

SOLUCIÓN 1ª

1 – Se realizará un cambio de plano de las dos superficies, en el que la segunda línea de tierra será paralela a la cara EFD de la cubierta. Con ello conseguimos las nuevas proyecciones de las dos superficies (nombradas con los subíndices 1).

2 – El ángulo formado por los faldones lo puedes medir en verdadera magnitud en ese cambio de plano ( E’1F’1D’1 )
3 – En el cambio de plano se ven los faldones proyectantes (de canto, de perfil, etc.) Luego la intersección de las aristas A-B-C es inmediata, es decir, son los puntos 3’1-4’1-5’1
4 – Medir las cotas de esos puntos y llevarlos a la proyección vertical.
5 – También se debe determinar donde la arista F corte a las caras laterales de la chimenea, puntos 1 y 2
6 – Por último se unen los puntos.

SOLUCIÓN 2ª

7 – Se trazan planos proyectantes auxiliares que contengan a las aristas A-B-C. Los planos pueden tener cualquier inclinación, pero yo por comodidad los he hecho paralelos a la cara D-E-F, los llamados P, Q y R

8 – Los puntos de corte de estos planos con las aristas D, E y F se suben a las proyecciones verticales de esas aristas y se unen para obtener las secciones de esos planos con la cubierta
9 – Donde las secciones corten a las aristas, puntos 3′-4′-5′, son las intersecciones de las aristas A’, B’ y C’ con los faldones
10 – También se debe determinar donde la arista F corte a las caras laterales de la chimenea, puntos 1 y 2
11 – Por último se unen los puntos.

SOLUCIÓN 3ª

12 – También se pueden utilizar planos que contengan a las misma caras de la chimenea. En ese caso se prolongan y los puntos de corte con la cubierta se suben a la otra proyección

13 – Donde esas secciones corten a las aristas A-B-C son 3′, 4′ y 5′
14 – También se debe determinar donde la arista F corte a las caras laterales de la chimenea, puntos 1 y 2
15 – Por último se unen los puntos.

SOLUCIÓN 4ª

16 – Para la determinación del ángulo de los faldones se puede recurrir a un cambio de plano como comente en el primer método o bien a un abatimiento de la cara DEF

---

Inicio > Sistema diédrico > Intersecciones de cuerpos en diédrico | |

Ejercicios de intersecciones de cuerpos – 996

Inicio > Sistema diédrico > Intersecciones de cuerpos en diédrico

Hallar la intersección de los dos prismas

---

SOLUCIÓN

Intersección de los prismas ABCD-EFGH y MNÑ-OPQ
1 – Las dos bases apoyadas sobre el plano horizontal, ABCD y MNÑ, se intersecan en los puntos 1 y 2

2 – Ahora averiguaremos la sección que produce la cara lateral derecha del prisma cuadrangular, CB-FG, que está de perfil sobre el prisma triangular.
Para ello llevamos los dos cuerpos al perfil y los puntos 2, 3 y 4, donde el plano (supuesto infinito) corta a las aristas de prisma triangular.
Uniendo, en el perfil, 3" con 4" y una paralela por 2" se obtienen las secciones (ilimitadas), siendo solo solución la parte que está sobre la cara CB-FG, es decir, los segmentos 5"-6" y 7"-8".
Estos puntos se llevan a ambas proyecciones.
3 – Se determinará donde la arista MO penetra en el prisma cuadrangular. Esto es inmediato en el perfil, donde m"-o" se ve que atraviesa a las caras c"d"-g"h" y a"b"-e"f", en los puntos 9" y 10"
4 – Idéntico procedimiento se hace con la arista NP, que nos da el punto 11"
5 – Uniendo los puntos que estén en una misma cara se determina la sección (línea negra), de recorrido 1-9-7-8-10-11-6-5-2-1

---

Inicio > Sistema diédrico > Intersecciones de cuerpos en diédrico | |

Ejercicios de intersecciones de cuerpos – 995

Inicio > Sistema diédrico > Intersecciones de cuerpos en diédrico

Dada la representación en proyección diedricá de la figura C, completar la intersección entre el cilindro y el prisma de base hexagonal.

---

SOLUCIÓN

En estos casos se utilizan planos horizontales, frontales u otros, que den una sección sencilla para los dos cuerpos. Los puntos de intersección de ambas secciones son los puntos de la intersección. En este caso en concreto :

1 – Trazar un plano frontal, p1

2 – La sección que produce el plano, p1, en el cilindro es una circunferencia que coincide con la proyección vertical de este
3 – La sección que produce el plano, p1, en el prisma son dos generatrices (rectas) que se obtienen llevando el plano al perfil (prolongarlo) y midiendo la distancia x1 entre el eje y los puntos de corte. Esa distancia, x1, se lleva a la proyección vertical, a partir de la parte central del prisma y hacia ambos lados trazando por ahí dos generatrices paralelas a las aristas del prisma
4 – Donde las dos secciones se corten entre sí, puntos 1′-2′-3′-4′, son cuatro puntos de la intersección buscada
5 – Bajar los puntos al plano, 1-2-3-4
6 – Repetir con más planos (en mi dibujo solo he hecho uno) para obtener más puntos.
7 – Unir los puntos

---

Inicio > Sistema diédrico > Intersecciones de cuerpos en diédrico | |

Ejercicios de intersecciones de cuerpos – 994

Inicio > Sistema diédrico > Intersecciones de cuerpos en diédrico

Dadas tres cuñas biseladas triangulares macizas que se cortan.

Completar las tres vistas diédricas con la intersección de las mismas.

---

SOLUCIÓN

La perspectiva es esta :

Y su alzado este :

Las otras dos vistas son simétricas al alzado :

---

Inicio > Sistema diédrico > Intersecciones de cuerpos en diédrico | |

Ejercicios de intersecciones de cuerpos – 993

Inicio > Sistema diédrico > Intersecciones de cuerpos en diédrico

Hallar la intersección de los dos conos siguientes :
Cono 1 : De revolución con vértice W(-65, 120, 15), centro O(25, 0, 35) y radio 30 mm.
Cono 2 : De revolución con vértice V(0, 40, 57) y radio de la base 35 mm, estando situado en el plano horizontal.

---

SOLUCIÓN

1 – Se dibujan las proyecciones de ambos conos.

2 – Se hace un primer cambio de plano del cono (cono coloreado en magenta) de eje WO con la segunda línea de tierra paralela a su eje. Mediante un segundo cambio de plano o una sección rebatida (la semicircunferencia en magenta las oscuro) se tiene la base del cono en verdadera magnitud.
3 – Se divide la base del cono (la rebatida) en varias partes. Yo solo he marcado una, a1, para ganar en claridad.
4 – Se determinan las proyecciones de esas divisiones en las otras vistas; a1′ en el primer cambio de plano, a en la proyección horizontal y a’ en la vertical, mediante el alejamiento Z1 y la cota Z2.
5 – Uniendo el punto A con el vértice del cono, W, se tiene una generatriz.
6 – Hallar la traza vertical, VA, de esta generatriz, WA.
7 – Unir los vértices de los dos conos, V-W.

8 – Determinar las trazas horizontal, th, y vertical, tv’, de la unión de los vértices de los conos, VW.
9 – Unir la traza vertical, tv’, con la traza vertical Va’ hasta la línea de tierra y desde ahí con la traza horizontal th. Esto nos da el plano PA.
10 – Donde la traza horizontal, pa, del plano corte a la base del cono de vértice V, puntos 1a y 2a, se unen con su vértice v.
11 – Donde estas últimas corten a la generatriz WA son los puntos de la intersección buscada, 1 y 2.
12 – Llevar las generatrices a la proyección vertical para determinar sus proyecciones verticales, 1′ y 2′.
13 – Repetir con el resto de las divisiones para obtener más puntos.

---

Inicio > Sistema diédrico > Intersecciones de cuerpos en diédrico | |

Ejercicios de intersecciones de cuerpos – 992

Inicio > Sistema diédrico > Intersecciones de cuerpos en diédrico

Dado el croquisacotado de la figura, se pide completar las vistas.

---

SOLUCIÓN

Determinación de la intersección de una pirámide triangular equilátera recta con un cilindro recto (punta afilada a la izquierda de la pieza)
1 – Tomar un plano de perfil, P

2 – Donde la traza vertical del plano, p’, corta a la prolongación de la arista de la pirámide (punto A’) se lleva al perfil (punto A") y por ahí se traza la sección que produce el plano en la pirámide (triángulo equilátero homotético de X"-Y"-Z")
3 – Donde la sección de la pirámide (el triángulo que parte de A") corta a la sección del cilindro (la circunferencia mayor del perfil) son los puntos de la sección (puntos 1", 2", 3", 4", 5" y 6")
4 – Se llevan esos puntos a las proyecciones horizontal y vertical sobre las trazas del plano (puntos 2 y 3). Yo solo he dibujado un par de ellos por claridad del dibujo
5 – Repetir con varios planos más para obtener más puntos que se unen a mano alzada

---

Inicio > Sistema diédrico > Intersecciones de cuerpos en diédrico | |

Ejercicios de intersecciones de cuerpos – 991

Inicio > Sistema diédrico > Intersecciones de cuerpos en diédrico

Trazar las vistas de la siguiente pieza, completando sus intersecciones.

---

SOLUCIÓN

En el sistema europeo o del primer diedro, las vistas serían :

En el sistema americano o del tercer diedro será :

La pieza es sencilla, la única dificultad es el trazado de la curva intersección entre el taladro vertical y el horizontal.

INTERSECCIÓN DE DOS AGUJEROS CILÍNDRICOS

Para hacer esta curva, se toman puntos cualesquiera en la planta (donde el agujero central superior se ve como una circunferencia)

Se levanta una vertical hasta el agujero semicircular que se ve en el alzado.
Por ahí se hacen horizontales.
En la planta se miden las medidas entre el agujero central superior y los laterales (medidas x, y, z)
Y estas medidas se llevan al perfil sobre las horizontales de cada punto.
Se repite con varios y se unen a mano alzada.
Comento como se lleva un punto a las distintas vistas :
En la planta eliges un punto de la circunferencia (marcado con A).

---

Inicio > Sistema diédrico > Intersecciones de cuerpos en diédrico | |