Inicio > Sistema diédrico > Intersecciones de cuerpos en diédrico
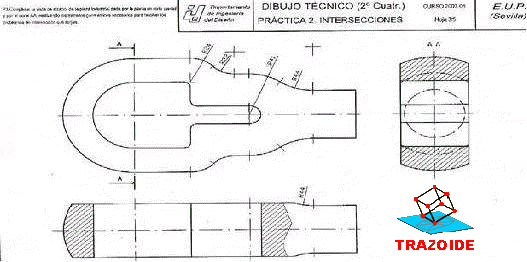
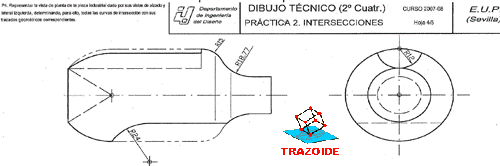
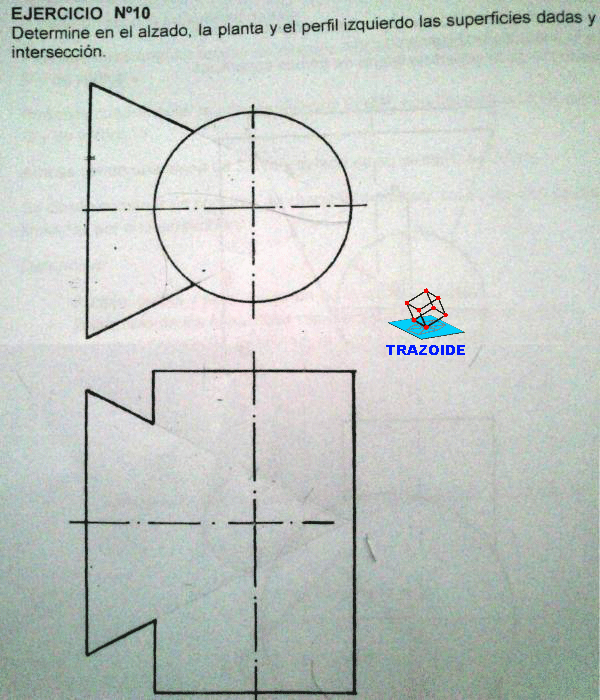
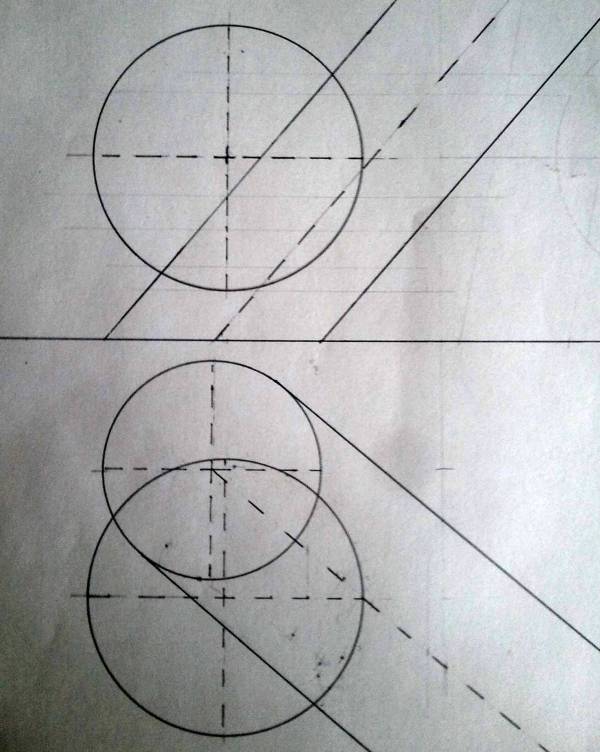
Resolver la intersección de las siguientes superficies:
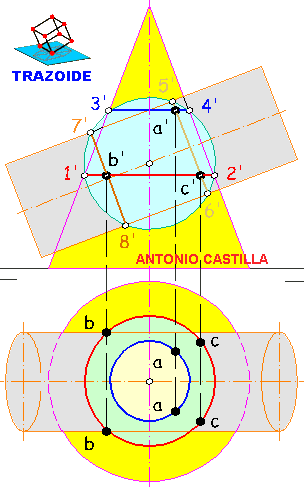
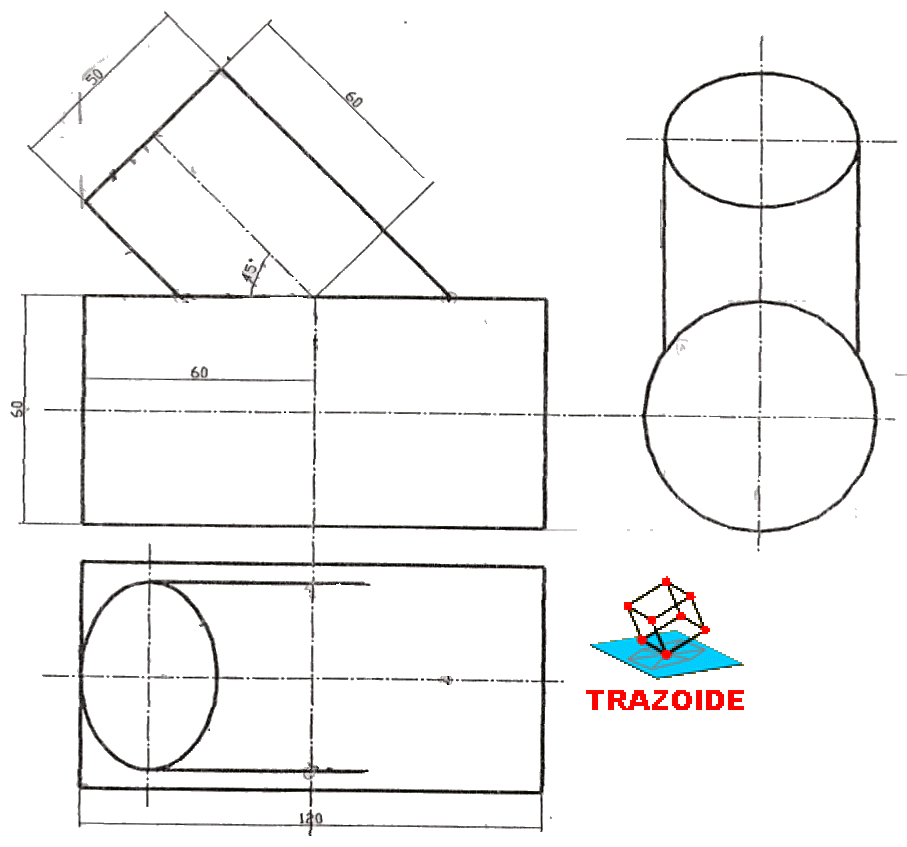
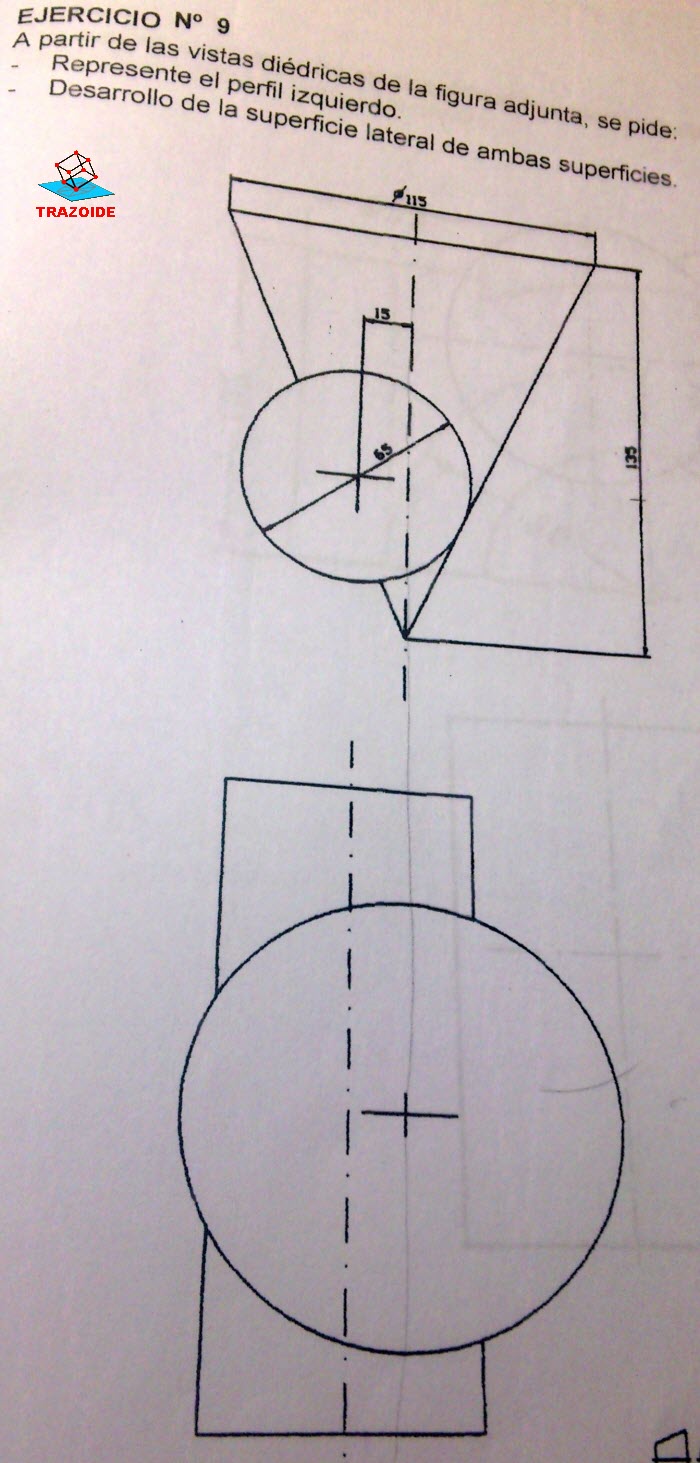
a) CONO DE REVOLUCIÓN de eje vertical, vértice V1 (0, 7, 12) y directriz circular en el PH, de 7 cm de radio.
b) SUPERFICIE CÓNICA DE REVOLUCIÓN, de vértice V2 (-7, 0, 0), apoyada en el plano horizontal de proyección a lo largo de una generatriz, cuyo eje se corta con el eje del primer cono en un punto de cota +4.
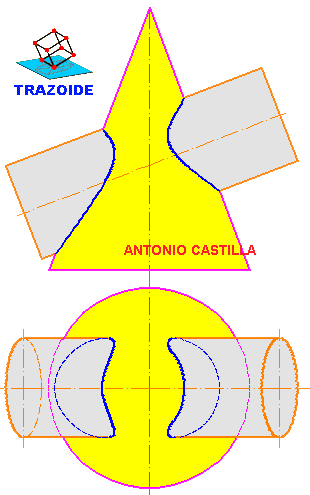
Indicar los puntos de paso por los contornos aparentes.
Ambas superficies están circunscritas a una tercera.
DATOS: Papel A3 horizontal, línea de tierra en el centro. Origen a 18 cm del borde izquierdo.
1 unidad = 1cm

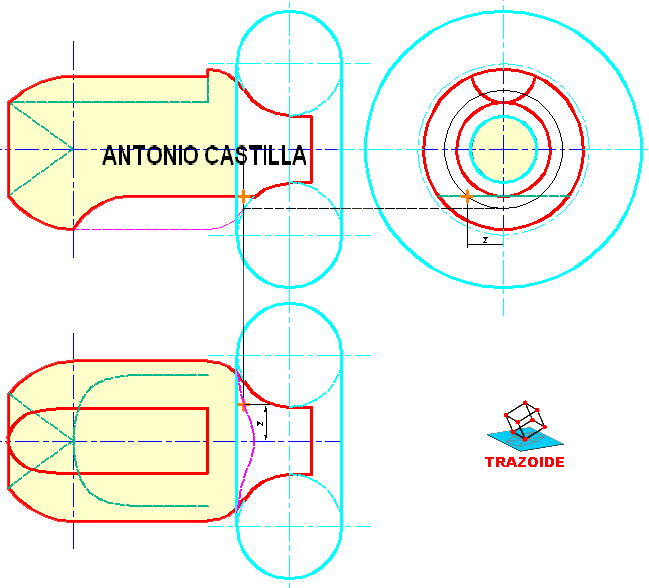
SOLUCIÓN
Para el primer cono no creo que tengas dificultad, no obstante te lo comento rápidamente :
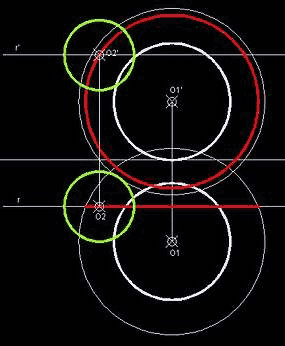
1 – Situar el vértice V1, el cual en proyección horizontal será a la vez el centro de la directriz, estando su proyección vertical sobre la línea de tierra.
2 – Con el radio dado dibujar una circunferencia en proyección horizontal y ya se tiene la proyección horizontal del primer cono.
3 – Llevar la medida del radio dado hacia ambos lados de la proyección vertical del centro (sobre la línea de tierra) y al unir esos extremos con el vértice V1 se consigue la proyección vertical del primer cono.
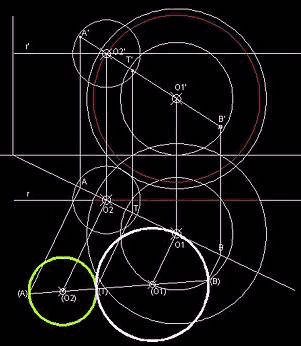
Para el segundo cono primero se dibuja primero el eje uniendo el vértice V2 con el punto del segundo eje de cota 4.
Para dejar bien determinado el segundo cono es necesario poner dibujar una directriz (una base).
Algunas de las formas más básicas (te las pongo en orden de dificultad o necesidad de mayores conocimientos) son :
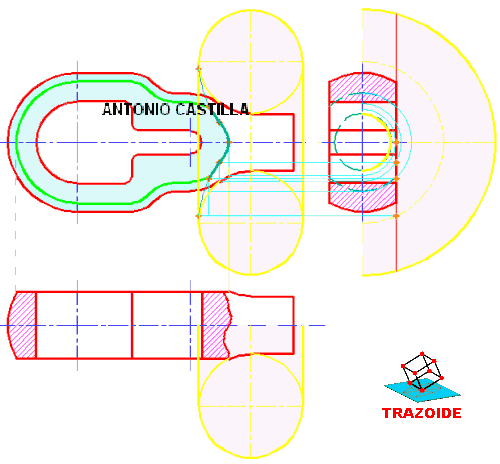
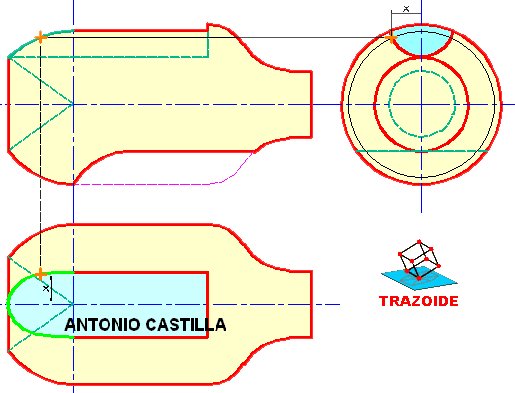
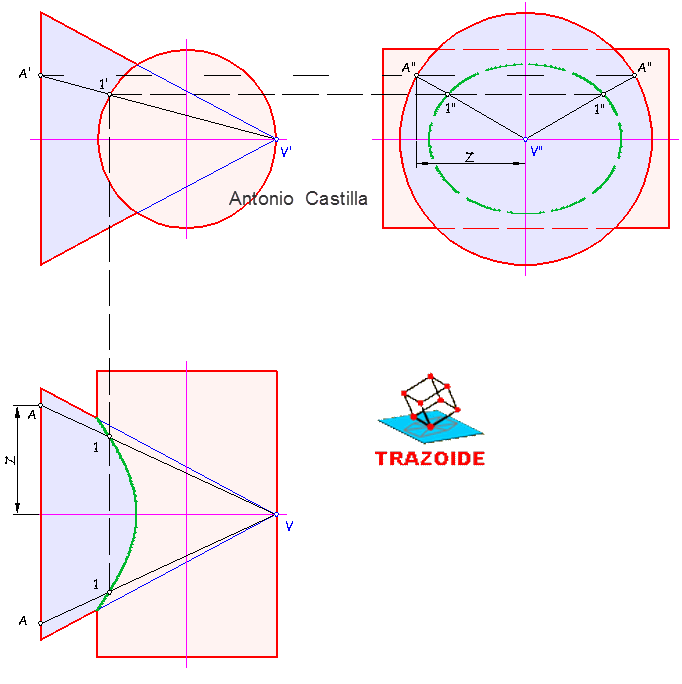
PRIMERA FORMA, mediante abatimiento.
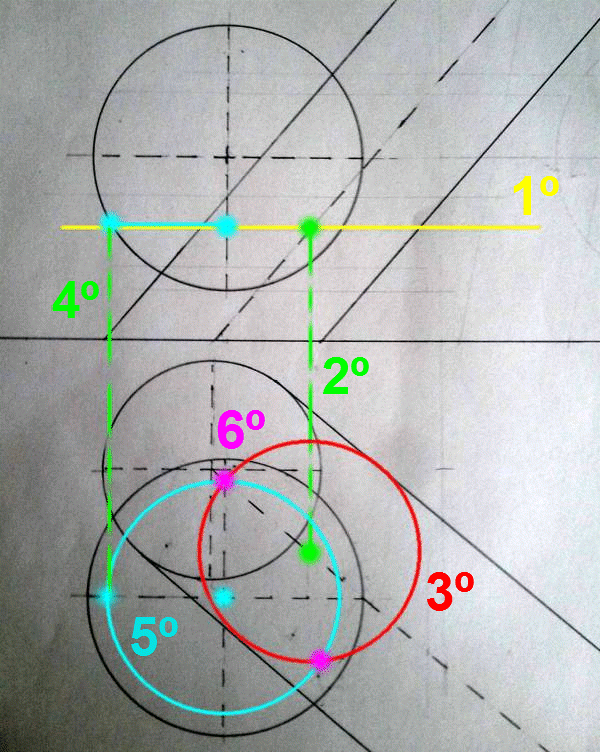
4 – Se elige un punto cualquiera del eje del segundo cono, al que llamaré C.
5 – Se dibuja un plano perpendicular al eje que pase por ese punto.
6 – Se abate el punto elegido, C, el cual será el centro de la circunferencia de la directriz que pasa por ese punto.
7 – El punto donde el eje del cono parece tocar a la traza horizontal del plano será el punto de contacto de dicha directriz con el plano horizontal. Luego, en el abatimiento se dibujará una circunferencia de centro C y radio hasta el punto descrito.
8 – Deshacer el abatimiento para obtener los puntos de la directriz
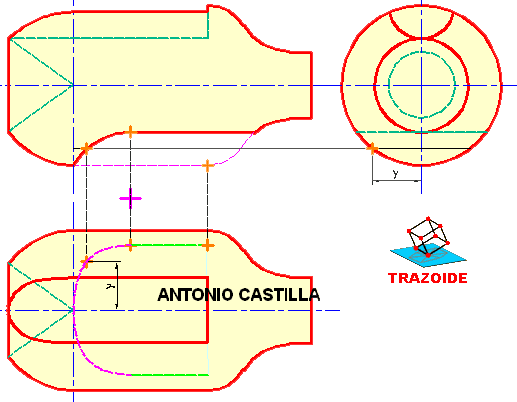
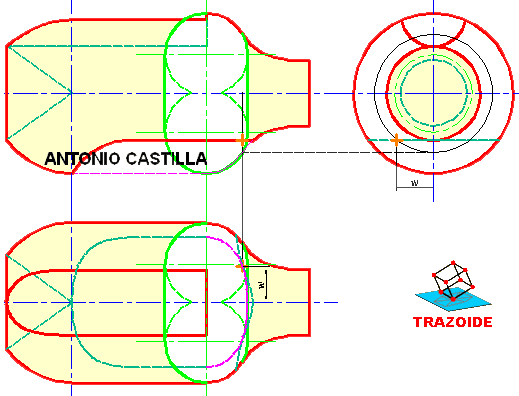
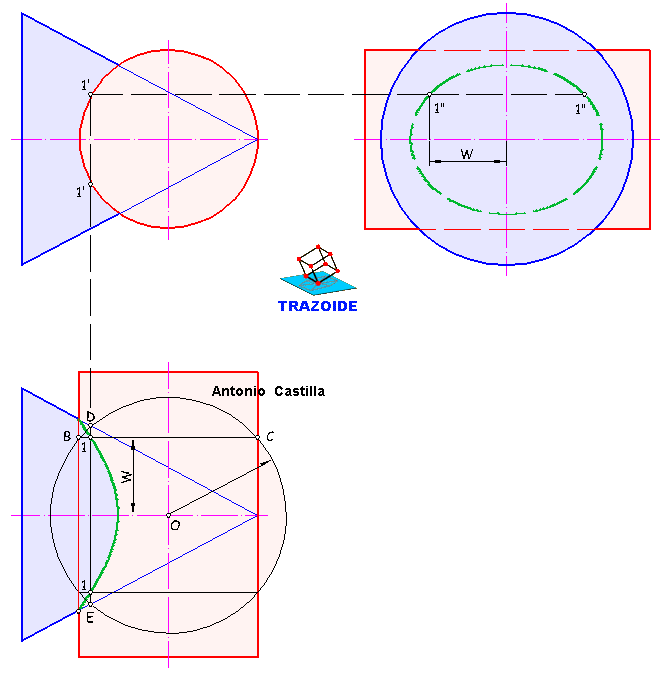
SEGUNDA FORMA, mediante cambio de plano.
9 – Se transforma el eje en una recta del tipo vertical mediante dos cambios de plano. En las dos últimas proyecciones el cono está situado en una posición igual a la del primer cono, es decir, con la directriz sobre el plano horizontal.
10 – En la penúltima proyección (primer cambio de plano) se elige un punto cualquiera sobre el eje, al que llamaré C.
11 – Por ese punto se hace una recta perpendicular al eje (directriz vista en posición horizontal) hasta que toque a la línea de tierra del primer cambio de plano.
12 – El punto donde toca a la línea de tierra es el punto de contacto de la directriz del cono sobre el plano horizontal de proyección.
13 – Luego, la distancia desde el centro C hasta ese punto es el radio de la directriz. En la última proyección (segundo cambio de plano), se dibujará una circunferencia con ese radio y ya se tiene la proyección horizontal cambiada de plano.
14 – Sobre la perpendicular al eje del primer cambio de plano se tiene la directriz.
15 – Basta con ir deshaciendo los cambios de plano de los puntos de la directriz.
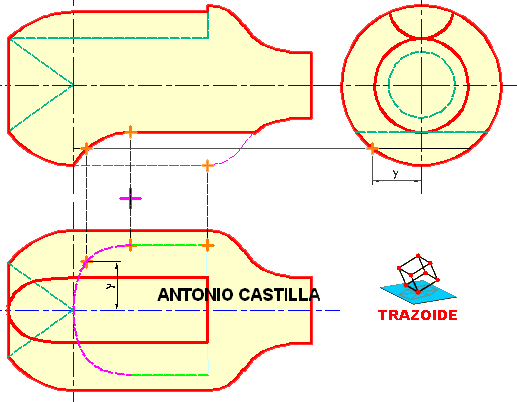
TERCERA FORMA, mediante cambio de plano y sección rebatida.
16 – En realidad este es el procedimiento anterior ligeramente simplificado para que no ocupe tanto espacio. Solo se hace un cambio de plano que transforme el eje en una recta del tipo frontal mediante un único cambio de plano.
17 – En el primer cambio de plano se elige un punto cualquiera sobre el eje, al que llamaré C.
18 – Por ese punto se hace una recta perpendicular al eje (directriz vista en posición horizontal) hasta que toque a la línea de tierra del primer cambio de plano.
19 – El punto donde toca a la línea de tierra es el punto de contacto de la directriz del cono sobre el plano horizontal de proyección.
20 – Luego, la distancia desde el centro C hasta ese punto es el radio de la directriz. Sobre esa misma perpendicular se dibujará una circunferencia con ese radio y ya se tiene la sección rebatida. En realidad no es más que un segundo cambio de plano (como el de antes) pero con la línea de tierra tercera sobre la misma directriz y trabajando solo con la diferencia de alejamientos.
21 – Basta con ir deshaciendo el cambio de plano de los puntos de la directriz.
CUARTA FORMA, mediante giro.
22 – La intención es la misma que el método de cambio de plano, colocar el cono con el eje en posición vertical o de punta mediante dos cambios de plano.
QUINTA FORMA, mediante giro y sección rebatida.
23 – Los razonamientos son los mismos que los del método de cambio de plano y sección rebatida pero mediante un giro que convierta al eje en horizontal o frontal.
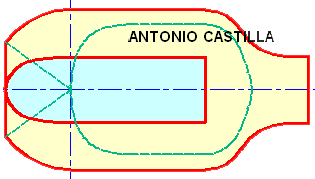
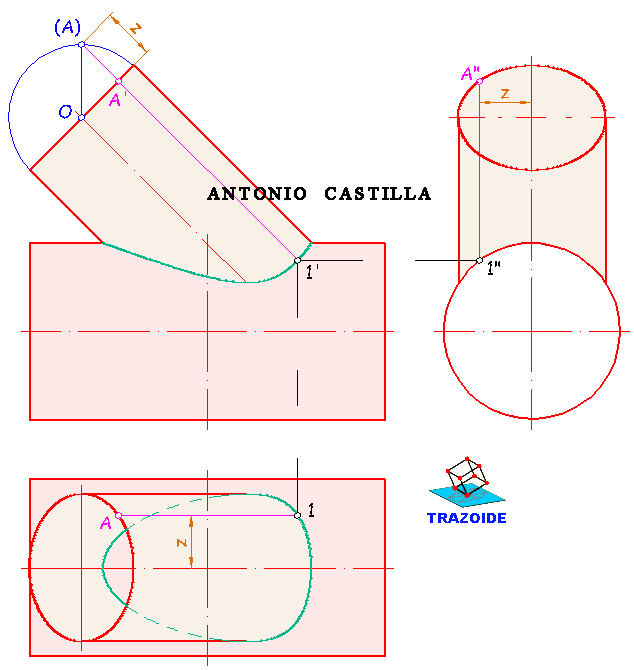
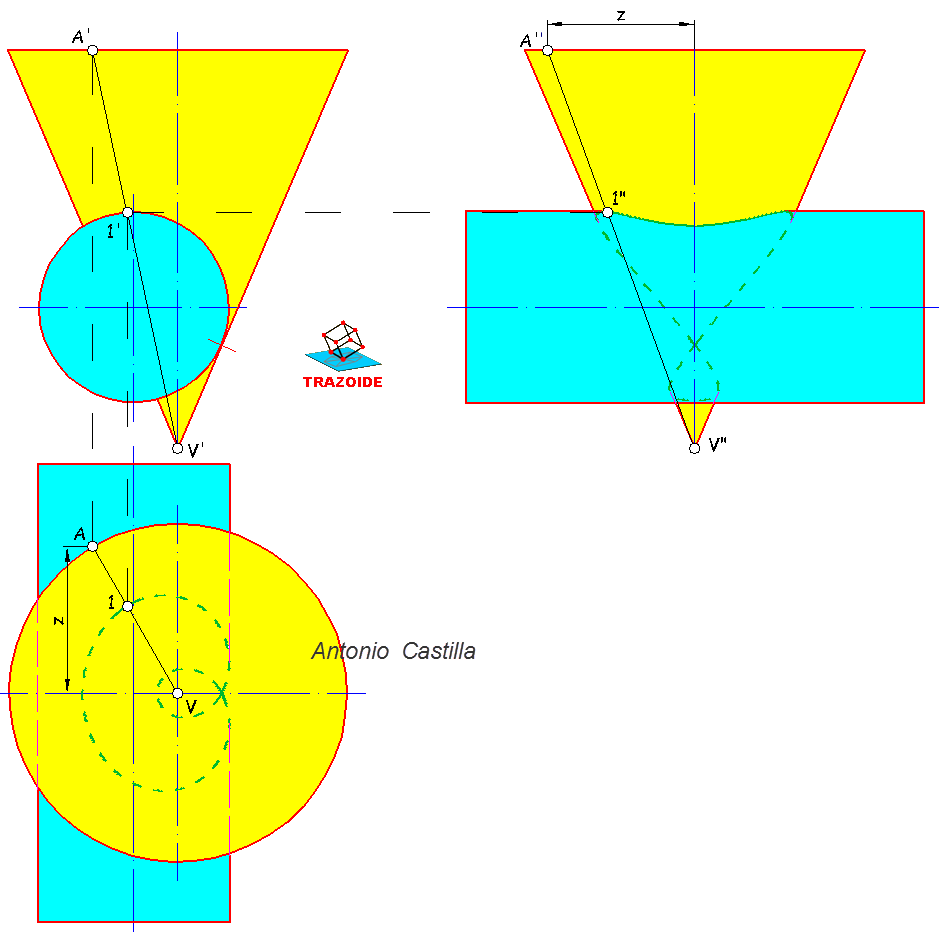
24 – La cuestión «Indicar los puntos de paso por los contornos aparentes, no la han expresado de una manera clara, pero lo que quieren decir, es que determines de forma exacta los puntos de contacto de las generatrices del contorno del cono en la directriz.
25 – Si tampoco te ha quedado claro te lo digo de otra forma. Cuando has hecho la directriz (una circunferencia en verdadera magnitud, pero una elipse en proyección) se hacen dos líneas que saliendo de su vértice V2 son tangentes a esa base, luego, se trata de hallar las tangentes a una elipse desde un punto y sus puntos de contacto (pero bien, nada de apoyar una regla donde cada uno quiera), pues esos dos puntos son los que te piden.
26 – Para determinarlos es necesario conocer algún elemento de la elipse. En este caso lo más fácil es determinar sus ejes principales, que te recuerdo. El eje mayor es paralelo a la traza del plano que lo contiene y mide lo el diámetro de la circunferencia en verdadera magnitud. El eje menor es perpendicular a la traza del plano y está en proyección.
27 – Una vez conseguidos los dos ejes principales pasa a determinar las tangentes a la elipse desde un punto exterior a ella por cualquiera de los procedimientos que conoces.
Inicio > Sistema diédrico > Intersecciones de cuerpos en diédrico | |






intersecciones de cuerpos – 988