Ejercicios resueltos de intersecciones en diedrico – 984
Inicio > Sistema diédrico > Intersecciones planas en diédrico
Definidos dos triángulos ABC y DEF por sus proyecciones diédricas, se pide obtener la intersección entre ambos estudiando la visibilidad del conjunto.
Se puede ver el cálculo de las sombras de los dos triángulos pulsando aquí.

SOLUCIÓN
INTERSECCIÓN
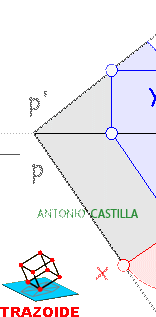
1 – Dibujar una paralela a la línea de tierra, r’-s’, en proyección vertical. Llevar los puntos de corte con los triángulos a la proyección horizontal y unirlos formando dos rectas r y s. Donde se corten ambas, punto g, es un punto de la intersección, llevarlo a la proyección vertical de r’-s’.
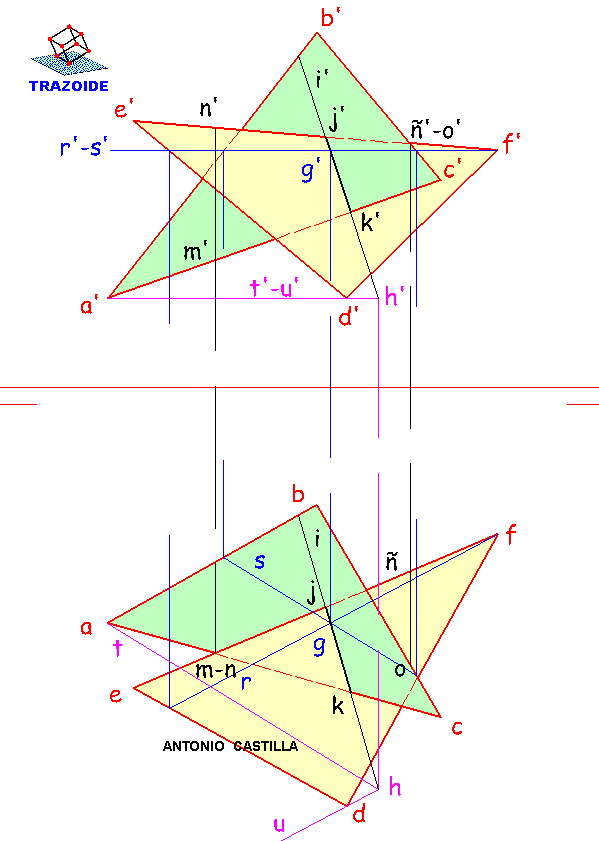
2 – Repetir con otra cualquiera, en mi caso t’-u’. El punto de corte de sus dos proyecciones horizontales, h, es otro punto de la intersección.
3 – Uniendo los dos puntos, G-H, se obtiene la intersección de los dos triángulos. En realidad, solo es intersección la parte común a los dos triángulos, es decir, J-K.
Aquí se han utilizado planos horizontales para hallar los puntos comunes, pero también se podría haber utilizado planos proyectantes que contengan a las aristas.
Visibilidad
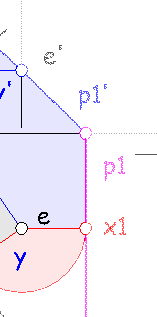
4 – Para determinar la visibilidad se elige un punto donde las dos proyecciones horizontales coincidan, como m-n, y se lleva a las proyecciones verticales de las dos rectas que lo forman, m’ sobre a’-c’ y n’ sobre e’-f’. En la proyección vertical n’ tiene mayor cota (está más alto) que m’, luego se deduce que la línea sobre la que está, e’-f’, está encima de a’-c’, por lo que e’-f’ será vista en proyección horizontal. Así, en proyección horizontal, a-m y e-n son vistos por ser contorno de la figura (o dicho de otra forma aquí no se tapan uno al otro por lo que los dos son vistos) y a partir de m-n la recta e-f es vista mientras que a-c es oculto (es decir uno se mete debajo del otro y el más bajo pasa a oculto), hasta llegar a la intersección de los dos triángulos, j-k, donde intercambian su visibilidad (por que la parte del triángulo abc que estaba debajo de efg lo atraviesa y pasa a ser visto) hasta que vuelven a ser contornos y pasan ambos a ser vistos (dejan de taparse).
5 – Esto se puede repetir con el resto de las líneas de la proyección horizontal o utilizar la lógica que es más rápido. Razónalo apoyándote en el coloreado de los triángulos.
6 – Para determinar la visibilidad de la proyección vertical se procede igual. En mi caso, elegí el punto ñ’-o’ en proyección vertical y se lleva a la proyección horizontal, ñ y o. Como o tiene más alejamiento (está más cerca del observador) que ñ esto implica que b-c está delante de e-f, por lo que b’-c’ tapará a e’-f’ en la proyección vertical. A partir de la intersección, j’-k’, cambian su visibilidad.
Inicio > Sistema diédrico > Intersecciones planas en diédrico | | Vídeos sobre intersecciones en diédrico