Mes: octubre 2014

Ejercicios de equivalencias – 986

Inicio > Geometría plana > Equivalencias

Dibujar un cuadrado equivalente al pentágono irregular dado

---

SOLUCIÓN

Existen varias formas. Una es dividiendo el pentágono en tres triángulos mediante sus diagonales. Después hallas cuadrados equivalentes a cada triángulo y por último un cuadrado suma de las áreas de los tres cuadrados. El segundo método es el que te expongo con más detenimiento.

SOLUCIÓN :

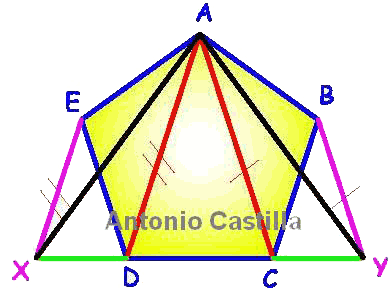
a1 – Designemos los vértices del pentágono como ABCDE. Unir dos vértices de lados contiguos, B y D por ejemplo.
a2 – Hacer una paralela a BD por C.
a3 – Donde corte a la prolongación de AB será el nuevo vértice X.
a4 – El pentágono se ha transformado en un cuadrilátero, el AXDE.
a5 – Repetir el proceso. Unir A con D.
a6 – Por E hacer una paralela a AD.
a7 – Donde corte a la prolongación de AX es el nuevo vértice Y.
a8 – El cuadrilátero queda transformado en un triángulo XDY.
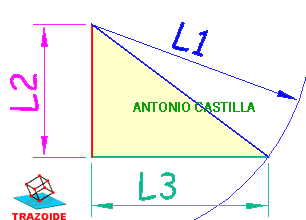
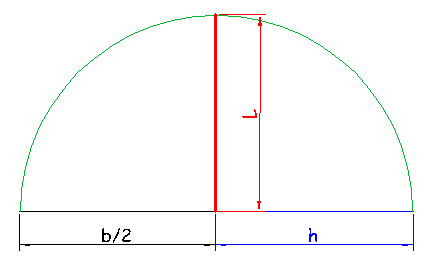
a9 – Hallar la media proporcional entre la mitad de la base de ese triángulo, XY/2, y su altura. Se está planteando (B/2) / L = L / H, donde B y H son la base y altura del triángulo y L el lado del cuadrado.
a10 – El resultado obtenido es el lado del cuadrado buscado.

---

Inicio > Geometría plana > Equivalencias | | Vídeos sobre equivalencias

Inicio > Geometría plana > Equivalencias

Hallar un cuadrado (lado L3) cuya área sea igual a la suma de otros dos conocidos (L1 y L2).

---

SOLUCIÓN

1 – Se plantea la igualdad de las áreas, S3 = S1 + S2. Y se sustituye por lo que valen (el cuadrado del lado), quedando L3² = L1² + L2².

2 – Esa expresión es la del teorema de Pitágoras, en la que los dos elementos que suman, L1 y L2, son los catetos de un triángulo rectángulo, y L3 la hipotenusa.

3 – Luego, para resolverlo se trazan dos líneas a 90º y sobre ellas se miden los lados de los cuadrados dados, L1 y L2. Uniendo sus extremos (hipotenusa) se consigue el valor del lado del cuadrado buscado, L3.

 

---

 

Inicio > Geometría plana > Equivalencias | | Vídeos sobre equivalencias

 

equivalencias – 985

Ejercicios de equivalencias – 984

Inicio > Geometría plana > Equivalencias

Hallar un cuadrado (lado L4) cuya área sea igual a la suma de otros tres conocidos (L1, L2 y L3)

---

SOLUCIÓN

1 – Se plantea la igualdad de las áreas, S4 = S1 + S2 + S3. Y se sustituye por lo que valen (el cuadrado del lado), quedando L4² = L1² + L2² + L3²
2 – Primero se plantea el cuadrado equivalente a la suma de las áreas de dos cualquiera de ellos (utilizando el método anterior), es decir, X² = L1² + L2². Así que se trazan dos líneas a 90º y sobre ellas se miden los lados de los cuadrados dados, L1 y L2. Uniendo sus extremos (hipotenusa) se consigue el valor del lado del cuadrado buscado, X.
3 – Se sustituye ese valor en la ecuación anterior L4² = ( L1² + L2² ) + L3² ⇒ L4² = X² + L3². Por lo que se plantea un nuevo Pitágoras cuyos catetos sean L3 y X. La hipotenusa es el lado L4 buscado
Esto se puede repetir tantas veces como se quiera (cuadrado equivalente a la suma de otros 4, 5, 6, etc).

---

Inicio > Geometría plana > Equivalencias | | Vídeos sobre equivalencias

Inicio > Geometría plana > Equivalencias

Hallar un cuadrado (lado L3) de área igual a la diferencia de las áreas de dos cuadrados de lados L1 y L2.

---

SOLUCIÓN

1 – Colocar el lado del cuadrado menor, L2.

2 – Hacer una recta perpendicular por uno de sus extremos.

3 – Con centro en el otro extremo y radio el lado del cuadrado mayor, L1, hacer un arco.

4 – Donde el arco corte a la perpendicular es el lado del cuadrado buscado, L3.

 

---

 

Inicio > Geometría plana > Equivalencias | | Vídeos sobre equivalencias

 

Ejercicios de equivalencias – 983

Inicio > Geometría plana > Equivalencias

Hacer un cuadrado equivalente al trapezoide (o cuadrilátero) dado

---

SOLUCIÓN

Para hacer un cuadrado equivalente al trapezoide dado, primero transformo el cuadrilátero en un triángulo equivalente, para ello uno dos de sus vértices, línea magenta, (te lo he dibujado aparte de la homología en el siguiente dibujo, para que esté más claro, pero se puede hacer encima) y se hace una paralela por el otro vértice, prolongando el lado contiguo se obtiene un triángulo equivalente (el que ves rayado), que tendrá de base la señalada como b y de altura la marcada con h.

Ahora se transforma el triángulo obtenido en un cuadrado, para ello se igualan las áreas b·h/2 = L·L, por lo tanto se conocen dos segmentos, b/2 y h, así que planteare una media proporcional para obtener el valor del lado del cuadrado, L (en el siguiente dibujo). La mitad de la base, b/2, y la altura, h, me han salido muy parecidas, pero no tienen por ser iguales.

---

Inicio > Geometría plana > Equivalencias | | Vídeos sobre equivalencias

 

     

Ejercicios de equivalencias – 981

Inicio > Geometría plana > Equivalencias

¿ Cómo se hace un triángulo equivalente a cuadrado de lado 4 cm ?

---

SOLUCIÓN

El enunciado en si no dice nada respecto del tipo de triángulo que se quiere.
Pasando a la parte práctica, existen varias formas, dependiendo de lo que desees, ya que al decir solo "triángulo equivalente" existen infinitas soluciones.

OPCIÓN 1

La forma más clásica (la que viene en todos los libros) es hacer un triángulo equivalente con la misma base que la del cuadrado. Para ello, basta con que unas los extremos de la base con cualquier punto que esté en una paralela separada el doble del lado del cuadrado. Se basa en que el área del triángulo es b·h/2, tomas como base, b, la del cuadrado, y como altura, h = 2·L, el doble del lado del cuadrado, pero cualquier punto a esa altura es válido. Si escoges el punto que está en la mediatriz de la base obtienes un triángulo isósceles.
También se podría hacer un triángulo de base el doble del lado del cuadrado y altura igual al lado del cuadrado.

OPCIÓN 2

Mediante una cuarta proporcional al igualar las áreas queda como L·L = b·h/2, o reordenado, L/b = (h/2)/L, o bien, L/h = (b/2)/L. Y ahora tienes dos opciones, dar un valor determinado a la altura y determinar la altura (primera ecuación) o bien al revés, decides cuanto valdrá la base y determinas la altura (segunda ecuación).

OPCIÓN 3

Mediante la determinación de un polígono equivalente con un lado menos. Dibujas una de las diagonales, haces una paralela por uno de los otros dos vértices, y donde corte a la prolongación del lado se une con el vértice opuesto.

---

Inicio > Geometría plana > Equivalencias | | Vídeos sobre equivalencias

Ejercicios de equivalencias – 980

Inicio > Geometría plana > Equivalencias

Construir un triángulo equivalente a un cuadrado de 50 mm. de lado

---

SOLUCIÓN

El triángulo ABE sí es equivalente al cuadrado, ya que su base es 2L y su altura L, por lo que su área valdrá b·h/2 = (2L)·(L)/2 = L·L, que es la misma área que la del cuadrado.

---

Inicio > Geometría plana > Equivalencias | | Vídeos sobre equivalencias

Ejercicios de equivalencias – 979

Inicio > Geometría plana > Equivalencias

Dan un lado y se debe hacer un pentágono regular y luego a partir de ese pentágono un triángulo del mismo área.

---

SOLUCIÓN

1 – Unir el vértice A con los opuestos C y D.
2 – Hacer paralelas a esa diagonales por B y E.
3 – Estas paralelas cortarán a la prolongación del lado CD en X e Y.
4 – Unir el vértice A con esos puntos de corte, X e Y, y ese es el triángulo equivalente, el AXY.

---

Inicio > Geometría plana > Equivalencias | | Vídeos sobre equivalencias

Ejercicios de equivalencias – 978

Inicio > Geometría plana > Equivalencias

Hallar un triángulo equivalente a un trapecio.

---

SOLUCIÓN

El triángulo tendrá por base una de longitud la mitad de la suma de las bases y de altura la misma del trapecio.

---

Inicio > Geometría plana > Equivalencias | | Vídeos sobre equivalencias

Ejercicios de equivalencias – 977

Inicio > Geometría plana > Equivalencias

Construir un triángulo equivalente a otro dado.

---

SOLUCIÓN

Trácese por el vértice opuesto a la base del triángulo conocido una paralela a ésta. Cualquier punto C’ de la paralela trazada, unido con los vértices de la base nos determina un triángulo equivalente al propuesto.

---

Inicio > Geometría plana > Equivalencias | | Vídeos sobre equivalencias