Mes: octubre 2014

Catenoide

es la superficie que se obtiene al girar una catenaria alrededor de una recta que no la corte y que sea perpendicular a su eje de simetría, siendo esta una superficie mínima de revolución.

Catenario

es la curva formada por una cadena o cuerda que cuelga libremente sujeta por sus extremos, y en la que solo actúa su propio peso.

En el siglo XVII, Galileo creyó que la curva que formaba una cadena sujeta por sus extremos era una parábola, aunque más tarde probo que estaba equivocado.

La palabra “catenaria” proviene del latín “catena”, que significa “cadena”. Esta curva girada hacia arriba da el arco catenario descubierto y usado por Gaudí, el cual es el arco ideal que aguanta su propio peso.

Girando la catenaria alrededor de una recta que no la corte y que sea perpendicular a su eje de simetría nace la superficie mínima de revolución llamada catenoide.

Su involuta es la tractriz.

A un catenario se le suele nombrar más como catenaria.

La catenaria, tiene gran aplicación en la ingeniería eléctrica para el diseño y colocación de líneas eléctricas, ya que los cables, al ser suspendidos, generan este tipo de curvas y su estudio permite determinar los esfuerzos a que serán sometidos por la acción de su propio peso. En la ingeniería civil se aplican en el diseño y construcción de puentes colgantes.

Sinónimos :

Catenario – Catenaria

Catenaria

es la curva formada por una cadena, cuerda o hilo que cuelga libremente sujeta por sus extremos, y en la que solo actúa su propio peso.

En el siglo XVII, Galileo creyó que la curva que formaba una cadena sujeta por sus extremos era una parábola, aunque más tarde probo que estaba equivocado.

La palabra “catenaria” proviene del latín “catena”, que significa “cadena”. Esta curva girada hacia arriba da el arco catenario descubierto y usado por Gaudí, el cual es el arco ideal que aguanta su propio peso.

Girando la catenaria alrededor de una recta que no la corte y que sea perpendicular a su eje de simetría nace la superficie mínima de revolución llamada catenoide.

A la catenaria también se la puede nombrar como catenario.

Su involuta es la tractriz.

La catenaria, tiene gran aplicación en la ingeniería eléctrica para el diseño y colocación de líneas eléctricas, ya que los cables, al ser suspendidos, generan este tipo de curvas y su estudio permite determinar los esfuerzos a que serán sometidos por la acción de su propio peso. En la ingeniería civil se aplican en el diseño y construcción de puentes colgantes.

Sinónimos :

Catenaria – Catenario

Forma de segunda categoría

son las constituidas por elementos de dos especies (puntos y rectas o rectas y planos).

Las más sencillas o fundamentales son :

a) La forma plana, es el conjunto de todos los puntos y rectas de un plano. Son figuras de esta forma la recta, las curvas planas y los polígonos.

b) La radiación, es el conjunto de las infinitas rectas y planos que pasan por un punto. Son figuras de esta forma el haz de rectas, el haz de planos, las superficies cónicas y las superficies piramidales.

Formas de primera categoría

son las constituidas por elementos de una sola especie (puntos o rectas o planos). Las más sencillas o fundamentales son :

a) La serie rectilínea o conjunto de los infinitos puntos de una recta. Son figuras de esta forma la recta y/o el segmento.

b) El haz de rectas, haz de rayos o radiación plana, es el conjunto de las infinitas rectas de un plano que pasan por un punto. Son figuras de esta forma un ángulo y el haz de rectas o rayos.

c) El haz de planos, es el conjunto de los infinitos planos que pasan por una recta. Son figuras de esta forma el ángulo diedro y el haz de planos.

En alemán :

• Ausdruck >> Forma

Categoría de una forma geométrica fundamental

es el número de condiciones necesarias para determinar cada elemento constituyente de manera inequívoca, dentro de la propia forma a la que pertenece.

Catastro

es la documentación escrita y cartográfica que determina y cuantifica la propiedad de la tierra con finalidades jurídicas, estadísticas, administrativas y fiscales.

Catametría

, se dice de los elementos que no son congruentes ni análogos, pero que son fruto de una común relación entre las figuras.

También se puede expresar como la unificación de las partes por una subparte en común, o sea es la coherencia de un conjunto de partes por una parte en común, ya sea tipográfica, gráfica, color, forma, etc.

Cualquier variante que permita una continuidad en las partes.

Inicio > Sistema axonométrico > Isométrica ||
Dibujar la letra A mayúscula en perspectiva isométrica.

SOLUCIÓN

Primero se debe dibujar el diseño de la letra sobre una cuadrícula rectangular. Estos son dos ejemplos de como podría ser :

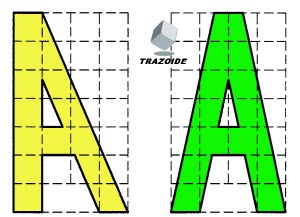
Después, sobre una cuadrícula isométrica, se llevan las medidas que se han obtenido del boceto en la cuadrícula rectangular. Dando profundidad tenemos la perspectiva isométrica, en este caso del segundo boceto (en verde) :

Inicio > Sistema axonométrico > Isométrica ||