Círculo de Furhmann
es el círculo que tiene por diámetro la recta que une el ortocentro de un triángulo con el punto de Nagel.
Mes: noviembre 2014
Círculo de Feuerbach
Círculo de Feuerbach
es el que tiene por diámetro la recta que une el circuncentro y el ortocentro de un triángulo, y cuya circunferencia pasa por los puntos medios de los lados del triángulo, por los pies de las alturas y por los puntos medios de las rectas que unen los vértices con el ortocentro.
También se le puede definir como el círculo que tiene como centro el punto medio del segmento de Euler y como diámetro la mitad de la circunferencia circunscrita al triángulo.
También se le denomina círculo de los nueve puntos o de Euler.
Sinónimos :
Círculo de las alturas – Círculo polar conjugado
Círculo de Euler
Círculo de Euler
es el que tiene por diámetro la recta que une el circuncentro y el ortocentro de un triángulo, y cuya circunferencia pasa por los puntos medios de los lados del triángulo, por los pies de las alturas y por los puntos medios de las rectas que unen los vértices con el ortocentro.
También se le puede definir como el círculo que tiene como centro el punto medio del segmento de Euler y como diámetro la mitad de la circunferencia circunscrita al triángulo.
También se le denomina círculo de los nueve puntos o de Euler.
Sinónimos : Circulo de Euler – Circulo de Feuerbach – Circulo de los nueve puntos
Círculo de distancias
Círculo de distancias
en el sistema central, el círculo de distancias es el círculo que tiene de centro el punto principal y de radio la distancia desde el plano de proyección al centro de proyección.
El círculo de distancias sirve para dejar definida la proyección, ya que sin él, existiría una misma proyección para distintos centros de proyección que estén a diferentes alturas.
Cómo saber si poner o no aristas en una cara
Inicio > Sistema axonométrico > Isométrica ||
Algunas personas se quedan con la duda de colocar o no determinadas aristas sobre una cara, sin tener claro si existen o no.
Por ejemplo, en la perspectiva isométrica planteada para estas tres vistas :
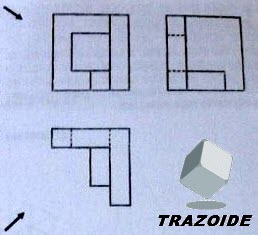
SOLUCIÓN
Una solución propuesta muy habitual es esta :
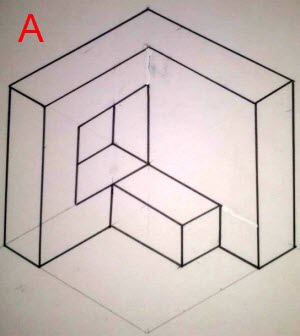
A esa solución le falta la línea gruesa naranja y le sobran las líneas gruesas amarilla y azul.
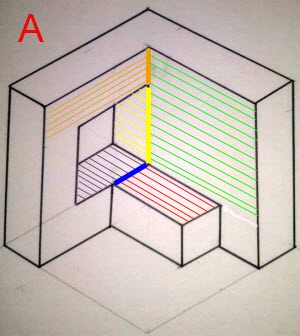
A veces es útil visualizar los planos que forman las caras dibujando líneas paralelas, que para mí son como la huella que va dejando el dedo (o lo que se siente) al deslizarlo por la pieza.
Dibujamos una línea donde hay una arista, es decir, la intersección de dos planos.
La línea gruesa naranja es la intersección (rincón) entre el plano formado por las líneas finas naranjas y verdes.
Sin embargo, la línea gruesa amarilla sobra porque los planos formados por las líneas finas verdes y amarillas están unas a continuación de otras por lo que no hay ninguna arista entre ellas.
Lo mismo ocurre con las líneas finas rojas y azules, forman un único plano y no dos, por lo que no hay ninguna línea de separación entre ellas (la línea gruesa azul, que se debe quitar).
<<< PROBLEMA ANTERIOR – – – – – PROBLEMA SIGUIENTE >>>
Inicio > Sistema axonométrico > Isométrica
isometrica-919
Círculo
Círculo
, a diferencia de la circunferencia, el círculo es una superficie plana limitada por una circunferencia; o lo que es lo mismo, es una porción de plano cuyo límite es una circunferencia.
La longitud de una circunferencia es L = 2·π·R, donde π es 3’1415 y R el radio.
Al proceso de hallar la longitud de la circunferencia de una forma gráfica se le llama rectificar.
No se debe confundir una circunferencia con un círculo.
El círculo es la zona interior de la circunferencia, y por lo tanto, un círculo es una superficie mientras que una circunferencia es una línea.
En la práctica mucha gente utiliza el término círculo para todo. La superficie de un círculo es S = π·R2, con los mismos significados anteriores. Un proceso muy clásico es el de hallar un cuadrado con la misma superficie del círculo, a esto se le llama la cuadratura del círculo.
También se denomina círculo al movimiento completo de un radio de circunferencia; pues, describe una porción de plano de naturaleza circular, en la que su contorno es la propia circunferencia.
Trapecio circular
Trapecio circular
es la porción de plano limitada por dos circunferencias concéntricas y dos radios distintos.
Segmento circular
Segmento circular
es la región circular (de círculo) comprendida entre un arco y su cuerda.
Sector circular convexo
Sector circular convexo
es la menor (de las dos posibles) regiones circulares comprendidas entre un arco y los dos radios que terminan en sus extremos.
A la de mayor superficie se la denomina sector circular cóncavo.
Sector circular cóncavo
Sector circular cóncavo
es la mayor (de las dos posibles) regiones circulares comprendidas entre un arco y los dos radios que terminan en sus extremos.
A la de menor superficie se la denomina sector circular convexo.