Otra de las aplicaciones de la cuarta proporcional es determinar el cuadrado de un segmento, x = a².
Otros enlaces relacionados :
Estás en : Geometría plana > Proporcionalidad
Cuadrado de un segmento x = a²
Autor: Administrador
Raíz cuadrada de un segmento
La raíz cuadrada de un segmento se determina mediante una media proporcional entre un segmento que mida una longitud igual a la raíz que se quiere obtener y una unidad. La unidad debe ser igual que la del segmento, es decir, si el segmento mide 9 cm la unidad es 1 cm, pero si el segmento es 90 mm la unidad es 1 mm.
Otros enlaces relacionados :
Estás en : Geometría plana > Proporcionalidad
Romboide conocidos sus lados y un ángulo
En este vídeo veremos como construir un romboide conocidos sus lados (con dos son suficientes porque los otros dos son iguales) y uno de sus ángulos.
Un romboide es el cuadrilátero (cuatro lados) que tiene los lados paralelos dos a dos y los ángulos iguales dos a dos, pero sus diagonales son distintas.
Los romboides también son conocidos como paralelogramos cualquiera.
Estás en : Geometría plana > Polígonos > Cuadriláteros > Paralelogramos > Romboides
Romboide conocidos sus lados y una altura
En este vídeo veremos como construir un romboide conocidos sus lados (con dos son suficientes porque los otros dos son iguales) y una de sus alturas.
Un romboide es el cuadrilátero (cuatro lados) que tiene los lados paralelos dos a dos y los ángulos iguales dos a dos, pero sus diagonales son distintas.
Los romboides también son conocidos como paralelogramos cualquiera.
Ejercicios de romboides
Estás en : Geometría plana > Polígonos > Cuadriláteros > Paralelogramos > Romboides
Romboide conocidos sus lados y una diagonal
En este vídeo veremos como construir un romboide conocidos sus lados (con dos son suficientes porque los otros dos son iguales) y una de sus diagonales.
Un romboide es el cuadrilátero (cuatro lados) que tiene los lados paralelos dos a dos y los ángulos iguales dos a dos, pero sus diagonales son distintas.
Los romboides también son conocidos como paralelogramos cualquiera.
Ejercicios de romboides
Estás en : Geometría plana > Polígonos > Cuadriláteros > Paralelogramos > Romboides
Visibilidad de una recta de perfil
Para determinar las trazas de una recta de perfil es necesario dibujarla en el perfil y ahí determinar donde atraviesa al plano horizontal y vertical para después llevarla a las proyecciones horizontal y vertical.
Solo es visible la parte de la recta que está en el primer diedro. Las trazas son necesarias para determinar donde atraviesa los cuadrantes y por tanto que parte no es visible.
Otros enlaces relacionados :
Estás en : Sistema diédrico > Rectas en diédrico
Trazas de una recta de perfil
Para determinar las trazas de una recta de perfil es necesario dibujarla en el perfil y ahí determinar donde atraviesa al plano horizontal y vertical para después llevarla a las proyecciones horizontal y vertical.
Otros enlaces relacionados :
Estás en : Sistema diédrico > Rectas en diédrico
Bisectriz de dos rectas que se cortan fuera de los límites del papel, mediante homotecia
La bisectriz de un ángulo lo divide en dos partes iguales y uno de los métodos para hallarlos es haciendo un arco con centro en el vértice (punto de corte de las dos rectas), pero este punto muchas veces es inaccesible. Aquí se explica una de las formas de resolverlo, mediante homotecia.
Otros enlaces relacionados :
- Vídeos sobre trazados fundamentales o básicos en dibujo técnico
- Ejercicios sobre trazados fundamentales o básicos en dibujo técnico
Estás en : Geometría plana > Trazados básicos
Bisectriz de dos rectas que se cortan fuera de los límites del papel, mediante bisectrices
La bisectriz de un ángulo lo divide en dos partes iguales y uno de los métodos para hallarlos es haciendo un arco con centro en el vértice (punto de corte de las dos rectas), pero este punto muchas veces es inaccesible. Aquí se explica una de las formas de resolverlo, mediante bisectrices.
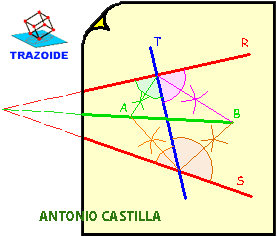
Otros enlaces relacionados :
- Vídeos sobre trazados fundamentales o básicos en dibujo técnico
- Ejercicios sobre trazados fundamentales o básicos en dibujo técnico
Estás en : Geometría plana > Trazados básicos
Transportar un ángulo con el compás
Transportar un ángulo consiste en copiarlo en otro lugar. No es necesario medir o conocer su valor.
Otros enlaces relacionados :
- Vídeos sobre trazados fundamentales o básicos en dibujo técnico
- Ejercicios sobre trazados fundamentales o básicos en dibujo técnico
Estás en : Geometría plana > Trazados básicos