Mes: octubre 2014

Inicio > Sistema diédrico > Abatimiento

 

Selectividad Andalucía
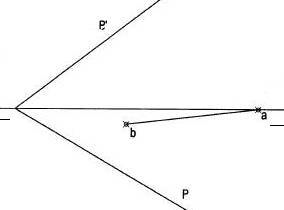
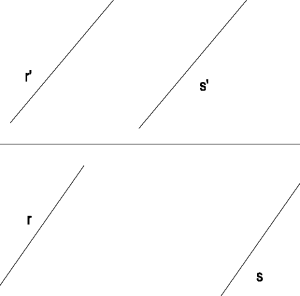
Dadas las proyecciones de las rectas R y S se pide :

1 – Hallar las trazas del plano P que contiene a las rectas R y S.

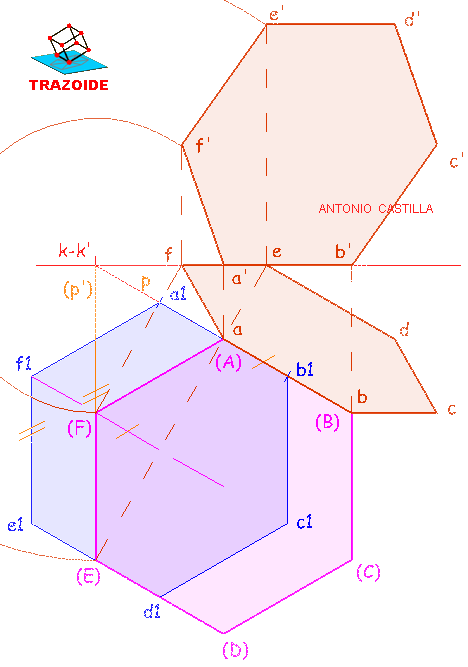
2 – Dibujar las proyecciones del hexágono regular que tiene dos de sus lados opuestos sobre las rectas R y S y uno de sus vértices sobre el plano horizontal de proyección, estando situado dicho polígono en el primer diedro de proyección.

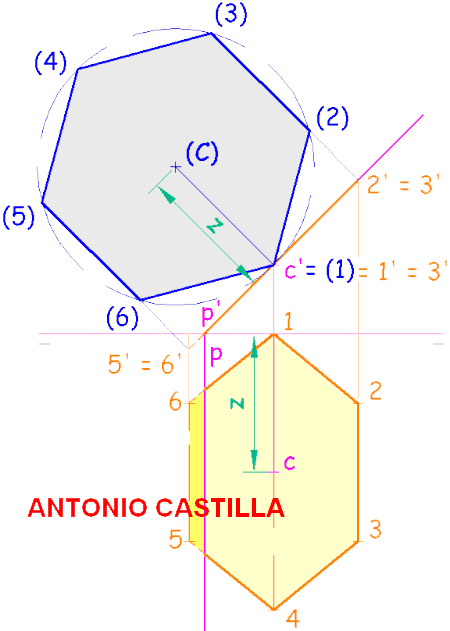
3 – Determinar las proyecciones de la pirámide regular de base el hexágono obtenido, altura 70 mm, y situada en el primer diedro de proyección.

---

SOLUCIÓN

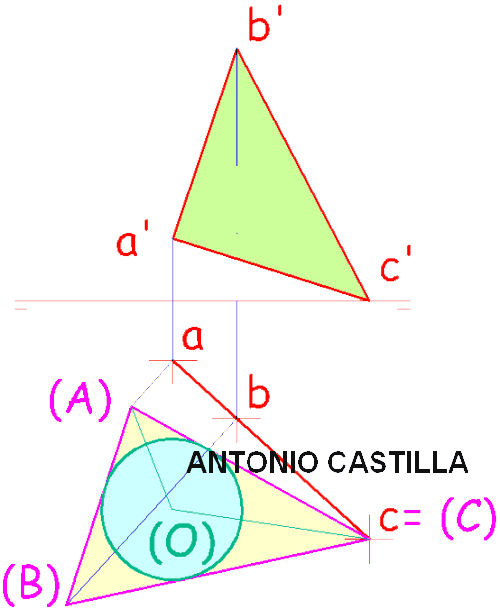
Hallar el plano formado por las dos rectas y abatirlo junto con las rectas.
Para hacer el hexágono en el abatimiento :
1 – Abatir las dos rectas R y S.

2 – A la mitad de la distancia que separa a R de S (en el abatimiento) se dibuja una paralela a R o S.

3 – Donde esta paralela media corte a la traza horizontal del plano es el primer vértice, A, del hexágono.

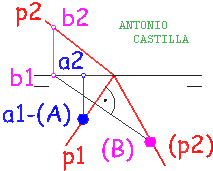
4 – Desde ese punto, A, levanta líneas que formen 30º con la paralela media, hacia ambos lados. Estas líneas cortarán a R y S en dos puntos que son dos vértices del hexágono, B y F, siendo además A-B o A-F el valor del lado del hexágono en verdadera magnitud.

5 – Sobre R y S, y a partir de B y F llevar una longitud igual a A-B o A-F, consiguiendo dos nuevos vértices, C y E.

6 – Con centro en C y E y radio A-B o A-F hacer dos arcos. Donde se corten es el último vértice, D, que deberá estar sobre la paralela media.

 

---

 

Inicio > Sistema diédrico > Abatimiento | | Vídeos sobre abatimientos

 

abatimientos en diédrico – 994

Ejercicios de abatimientos en diédrico – 993

Inicio > Sistema diédrico > Abatimiento

Selectividad Andalucía
Un trapecio rectángulo ABCD está contenido en un plano P, y se sabe que el segmento ab es la proyección horizontal de la base mayor de dicho polígono, que la altura BC es igual a 20 m y que la base menor CD es igual a 22 m. Se pide determinar las proyecciones diédricas del hexágono.

---

SOLUCIÓN

1 – Abatir el plano P y los puntos A y B.
2 – En el abatimiento :
2.a – Desde el punto B levantar una perpendicular a AB y sobre ella medir la altura del trapecio, 20 mm. Este punto es C.
2.b – Desde ahí una paralela a AB sobre la que se medirá el lado CD = 22, consiguiendo el cuarto vértice, D, de trapecio
3 – Desabatir los cuatro puntos del trapecio para determinar su proyección horizontal
4 – Hallar la proyección vertical de los cuatro puntos

---

Inicio > Sistema diédrico > Abatimiento | | Vídeos sobre abatimientos

Ejercicios de abatimientos en diédrico – 992

Inicio > Sistema diédrico > Abatimiento

Obtención de la traza horizontal de un plano, p, conocidas las proyecciones horizontal y vertical de un punto, a y a’, que está en el plano y el abatimiento del punto, (A).

---

SOLUCIÓN

1 – Unir el punto abatido, (A), con la proyección horizontal del punto, a
2 – Trazar una perpendicular a esta última por la proyección horizontal del punto
3 – Medir sobre esa perpendicular la cota del punto (entre la línea de tierra y la proyección vertical a’)
4 – Unir el extremo de la perpendicular con el punto abatido
5 – Determinar la mediatriz de este último segmento
6 – Por donde la mediatriz corte a la unión de la proyección horizontal con el punto abatido se dibuja una perpendicular a esa misma recta y esa es la traza horizontal del plano

---

Inicio > Sistema diédrico > Abatimiento | | Vídeos sobre abatimientos

Ejercicios de abatimientos en diédrico – 991

Inicio > Sistema diédrico > Abatimiento

Obtención de la traza horizontal de un plano, p, conocidas las proyecciones horizontal y vertical de un punto, a y a’, que está en el plano y el abatimiento del punto, (A)

---

SOLUCIÓN

1 – Colocar el punto K y desde él trazar una recta que forme 30º con la línea de tierra. Esta es la traza horizontal del plano que contiene al hexágono, p.

2 – Dibujar un hexágono, a1-b1-c1-d1-e1-f1, de lado 50 apoyado en la recta anterior y en cualquier lugar.
3 – Por K trazar una paralela a e1-f1. Esta es la traza vertical del plano abatida, (p’).
4 – Por f1 hacer una paralela a p y donde corte a (p’) es el vértice (F) del hexágono abatido buscado.
5 – Trazar el resto del hexágono abatido, (A)-(B)-(C)-(D)-(E)-(F), por paralelas al primero, a1-b1-c1-d1-e1-f1.
6 – Las proyecciones horizontales de A y B coinciden con sus abatimientos y las verticales están sobre la línea de tierra.
7 – Por (E) y (F) trazar perpendiculares a la traza horizontal del plano, p, y donde corten a la línea de tierra son sus proyecciones horizontales. Para las verticales subir perpendiculares a la línea de tierra y con centro en K y radios hasta los puntos abatidos, (E) y (F), trazar sendos arcos. Donde corten a las verticales son las proyecciones verticales.
8 – Unir las proyecciones de los puntos, B con A, A con F y F con E.
9 – El lado E-D es paralelo al lado A-B y de igual longitud. Por el extremo D una paralela al lado A-F y con su misma longitud se obtiene C. Unir C con B.

---

Inicio > Sistema diédrico > Abatimiento | | Vídeos sobre abatimientos

Inicio > Sistema diédrico > Abatimiento

Para situar una cámara fotográfica se dispone de un trípode cuyas patas miden como máximo 1’5 m.
Los únicos puntos de apoyo seguros para las patas del trípode están en los puntos A(-7, 2, 0), B(-3,  13,  0), C(10,  3,  0) en dm.
La cámara debe quedar para hacer las fotografías a una altura de 1 m respecto del plano horizontal. Para ello estiramos dos de sus patas al máximo y las colocamos en los puntos A y B.

Se pide :
a) ¿ Cuanto mide la tercera pata para obtener la altura deseada ?

b) Dibujar las proyecciones del trípode posicionado. El vértice se llamará V.

---

SOLUCIÓN

1 – Uniendo las proyecciones horizontales de los puntos A y B se tiene la traza del plano.

2 – Los puntos A y B ya están abatidos. A partir de ellos formar un triángulo isósceles de lado desigual A-B y lados iguales de 1’5 m. El tercer vértice es V, el punto buscado pero en el abatimiento.

3 – Hallar la proyección horizontal del punto V conocido su abatimiento y la cota del punto, 1 m.

4 – Determinar su proyección vertical con la cota conocida, 1 m.

Existe otro procedimiento mediante esferas, pulsar aquí para verlo.

 

---

 

Inicio > Sistema diédrico > Abatimiento | | Vídeos sobre abatimientos

 

abatimientos – 990

Ejercicios de abatimientos en diédrico – 989

Inicio > Sistema diédrico > Abatimiento

Un triángulo equilátero gira alrededor de su lado A(-70, 40, 30)-B(-35, 55, 70) hasta que su vértice C choca con el plano Q-Q´en su posición más alta posible. El plano Q-Q pasa por el punto N(-70, 0, 0) es paralelo a la recta t [(40, 0, 50);(75, 40, 50)] y forma 60º con el horizontal ascendiendo hacia la derecha. (x,y,z)

Dibujar las proyecciones diédricas del triángulo.

---

SOLUCIÓN

Para determinar el vértice C puede haber muchas opciones.

OPCIÓN I Por abatimiento

1 – Dibujar un plano, P, perpendicular a la recta AB y que pase por su punto medio, M.
2 – Hallar la intersección, I, entre el plano perpendicular a AB, P, y el plano Q.
3 – Aparte determinar el valor de la verdadera magnitud de la altura del triángulo equilátero. Para ello hallar primero la verdadera magnitud de AB y después dibujar un triángulo equilátero en el que se determinará su altura, h.
4 – Abatir el punto medio del lado AB, M, y la recta intersección, I, respecto del plano perpendicular a AB, P.
5 – En el abatimiento con centro en M y radio la altura del triángulo equilátero, h, se dibuja una circunferencia.
6 – Donde la circunferencia corte a la recta intersección, I, abatida son las posibles soluciones para el vértice C.
7 – Desabatir el punto C.

OPCIÓN II Por cambio de plano

8 – Dibujar un plano perpendicular a la recta AB y que pase por su punto medio.
9 – Hallar la intersección, I, entre el plano perpendicular a AB y el plano Q.
10 – Aparte determinar el valor de la verdadera magnitud de la altura del triángulo equilátero. Para ello hallar primero la verdadera magnitud de AB y después dibujar un triángulo equilátero en el que se determinará su altura, h.
11 – Hacer el cambio de plano necesario para que la recta AB se convierta en vertical o de punta.
12 – Cambiar, con las mismas líneas de tierra, la recta intersección, I.
13 – Con centro en la recta AB en el cambio de plano (donde se ve como un punto) y con radio la altura en verdadera magnitud del triángulo equilátero, h, se dibuja una circunferencia. Donde la circunferencia corte a la recta intersección, I, son las dos posibles soluciones para C en el cambio de plano.
14 – Determinar las proyecciones de C. Para ello en la penúltima proyección se traza una perpendicular a AB por su punto medio y se lleva la última proyección de C a esta perpendicular mediante una perpendicular a la última línea de tierra.

---

Inicio > Sistema diédrico > Abatimiento | | Vídeos sobre abatimientos

Ejercicios de abatimientos en diédrico – 988

Inicio > Sistema diédrico > Abatimiento

Cómo abatir un puntos que están en un plano oblicuo, P, y pertenecen al plano horizontal, A, o vertical, B, de proyección

---

SOLUCIÓN

1 – Si un punto, A, está en el plano horizontal y además pertenece a un plano oblicuo, si abates alrededor de la traza horizontal del plano su abatimiento coincide con la proyección horizontal del punto, (A) = A1.

2 – Si un punto, B, está en el plano vertical y además pertenece a un plano oblicuo, si abates alrededor de la traza horizontal del plano su abatimiento está sobre la traza vertical abatida. A partir de su proyección horizontal, B1, dibuja una perpendicular a la traza horizontal del plano y donde corte a la traza vertical del plano abatida es el abatimiento del punto, (B).

---

Inicio > Sistema diédrico > Abatimiento | | Vídeos sobre abatimientos

Ejercicios de abatimientos en diédrico – 987

Inicio > Sistema diédrico > Abatimiento

Un plano proyectante vertical forma 45º con el plano horizontal de proyección y pasa por O(0, 0, 0). Contiene un hexágono regular con dos lados horizontales, centrado en C(2, 4, x) y tal que uno de sus vértices toca a la traza vertical del plano. Dibujarlo, con partes vistas y ocultas

---

SOLUCIÓN

1 – Por el vértice, levanta 90º y 45º con la línea de tierra, para formar el plano (en magenta)

2 – Localizada la proyección horizontal del centro, c, la proyección vertical, c’, está sobre la traza vertical del plano, p’
3 – Se abate el centro, (C). Para ello se toma su alejamiento, z, y se lleva en perpendicular a la traza vertical del plano
4 – Con centro en (C) y radio hasta la traza vertical se traza una circunferencia
5 – El primer vértice del hexágono, (1), está donde la circunferencia toque a la traza del plano
6 – A partir de ese vértice se traza el hexágono
7 – Los puntos desabatidos están en perpendicular a la traza vertical del plano y sobre ella.
8 – La proyección vertical del hexágono se ve como una línea (naranja), siendo la parte que está por debajo de la línea de tierra, oculta.
9 – Se hallan las proyecciones horizontales de los seis puntos del hexágono (al revés de como se abatió el centro C)
10 – La parte del hexágono que pasa al otro lado de la traza del plano (zona amarilla más oscura) es oculta

---

Inicio > Sistema diédrico > Abatimiento | | Vídeos sobre abatimientos

Ejercicios de abatimientos en diédrico – 986

Inicio > Sistema diédrico > Abatimiento

Distancia entre el punto A y la recta R (mediante abatimiento).

---

SOLUCIÓN

A – Hacer un plano con la recta y el punto dado
B – Abatir la recta y el punto
C – En el abatimiento se traza una perpendicular a la recta que pase por el punto. Esa es la verdadera magnitud entre la recta y el punto

---

Inicio > Sistema diédrico > Abatimiento | | Vídeos sobre abatimientos

Ejercicios de abatimientos en diédrico – 985

Inicio > Sistema diédrico > Abatimiento

Dibujar una circunferencia inscrita en un triángulo ABC proyectante horizontal.

---

SOLUCIÓN

Debes de abatir el triángulo para poder hacer la circunferencia inscrita.
Debes de fijarte en que la proyección horizontal se ve como una línea, luego se trata de un plano proyectante.

En el abatimiento trazas un par de bisectrices y el punto de corte es el incentro.
El resto es desabatir.

---

Inicio > Sistema diédrico > Abatimiento | | Vídeos sobre abatimientos