Inicio > Sistema diédrico > Intersecciones de cuerpos en diédrico
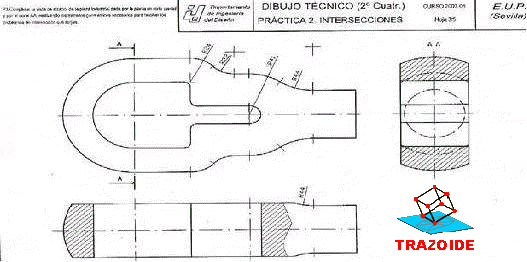
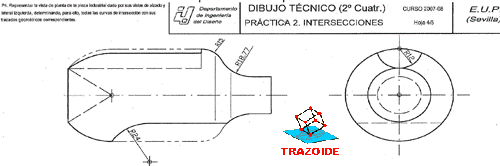
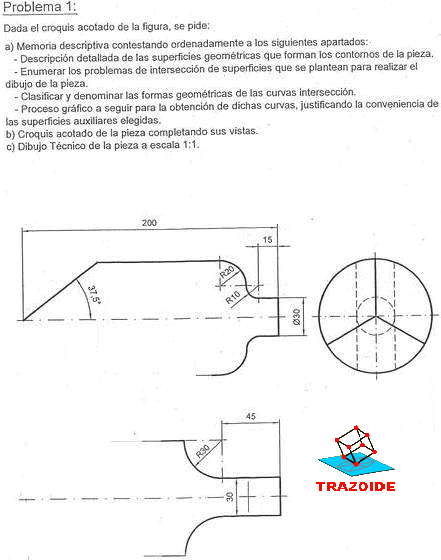
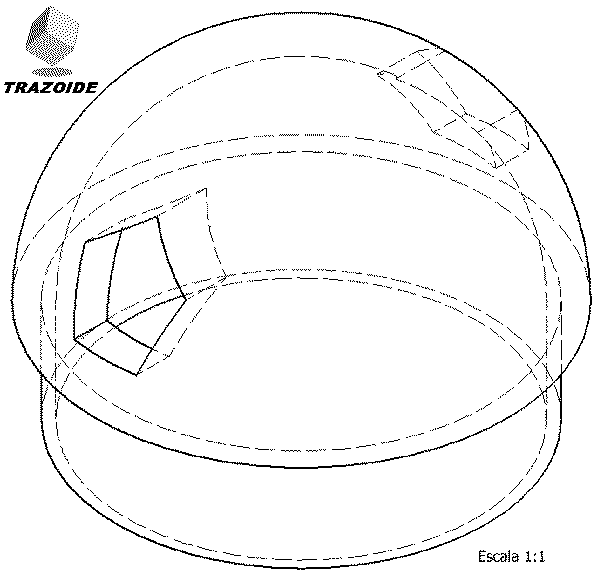
Dada la pieza representada en la figura dibujar, a lápiz y a la escala más apropiada al papel disponible, las seis vistas de la misma en sistema diédrico europeo. No es necesario tener en cuenta el coeficiente corrector 0.816.

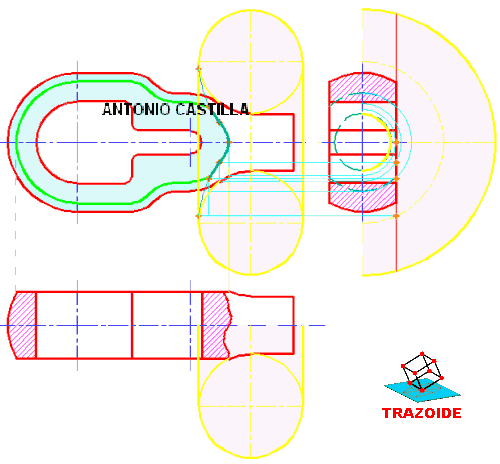
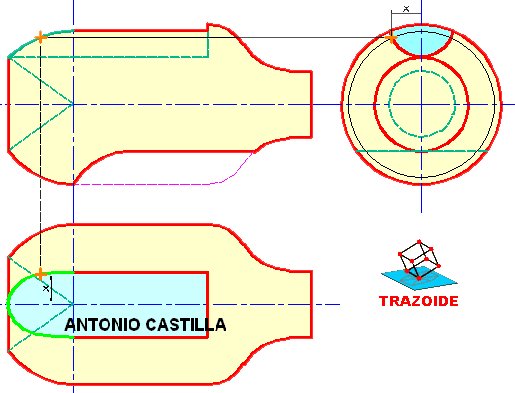
SOLUCIÓN
Ejes de la perspectiva.
1 – Primero situaré los ejes de la perspectiva. Las líneas verticales del contorno del cilindro (a la izquierda) las consideraré como dirección del eje Z.
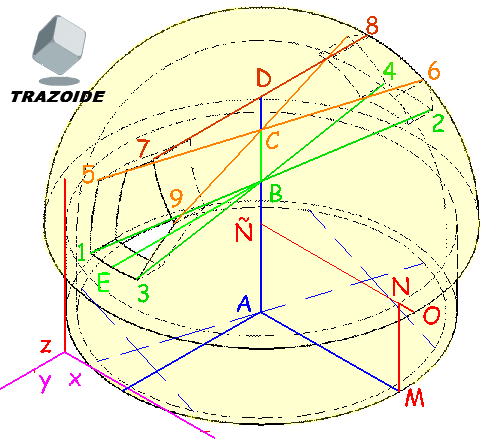
2 – Respecto de ese eje Z dibujaré los ejes X e Y formando 120º con el Z (en magenta a la izquierda).
Centros de las elipses.
3 – Para localizar el centro de la elipse inferior (la correspondiente al agujero cilíndrico) dibujo una cuerda cualquiera (a la derecha en línea azul discontinua fina) y otra paralela en cualquier lugar. Se unen sus puntos medios y se alarga hasta tocar a la elipse. Su punto medio es el centro de la elipse, A. Este procedimiento está explicado más detalladamente en este enlace (pulsar aquí).
4 – Por el centro A se dibujan los ejes de la perspectiva (en azul grueso).
5 – Para localizar el centro de las otras elipses se podría recurrir al mismo procedimiento o bien a trazar generatrices, como la que parte de M sube en paralelo hasta la siguiente, punto N. Esto nos da la altura del cilindro inferior M-N.
6 – Por N una paralela al eje X y donde corte al eje, Ñ, es el centro de la semiesfera y hasta donde toca a la elipse, O, es su radio, Ñ-O.
Centros del hueco pentagonal.
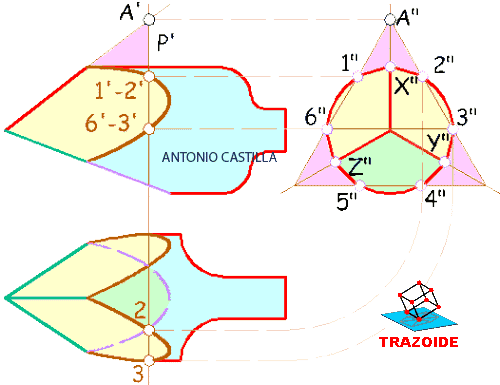
7 – Como los dos huecos pentagonales son simétricos se puede plantear una simetría. Es decir, se une el punto 1 con el punto 2 y donde corte al eje vertical que parte de A es el centro de la parte inferior del hueco pentagonal, B.
Otra forma sería dibujar la cuerda 1-3 y determinar su punto medio, E, y por él trazar una paralela al eje Y. Donde corte al eje Z es el centro B y además el radio de esa elipse, E-B, por estar sobre un eje.
8 – El radio de la circunferencia que tiene por centro a B no se puede medir hasta los puntos 1, 2, 3 o 4, ya que en un dibujo isométrico los radios de las elipses que están en verdadera magnitud son los paralelos a los ejes X, Y o Z. Por ello desde su centro B se dibuja una paralela a Y y donde toque a la elipse es su radio, B-E. En la práctica está medida es muy aproximada, será mejor emplear el procedimiento que describo más adelante.
9 – El centro de los siguientes puntos se logran de la misma forma. Unir 5 con 6 y donde corte al eje Z es su centro, C. El radio de la elipse que pasa por esos puntos, 5, 6 y 9, no se puede lograr como antes ya que ni siquiera está dibujada. Recurriremos al alzado para hallarlo.
10 – Para el vértice superior del hueco hexagonal, 7, dibujaré una paralela al eje Y y donde corte al eje Z es su centro D. En este caso sí se puede medir directamente entre D-7 por ser paralela al eje Y.
Radios exactos para el hueco pentagonal.
11 – Como conocemos las alturas en Z para los centros los radios se calculan de una forma exacta si se trabaja directamente sobre la vista. Dibujaré un alzado parcial (solo la parte que nos interesa ahora mismo). Este alzado está compuesto del cilindro exterior (un rectángulo con las medidas A-M y M-O) y la semiesfera (una semicircunferencia de radio Ñ-O).
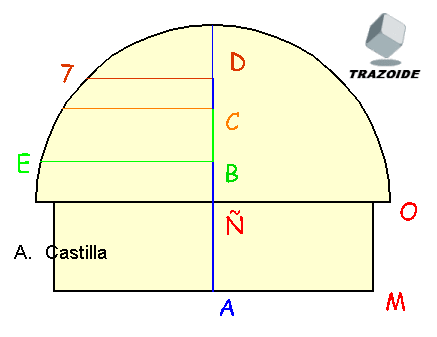
12 – Sobre su eje central se sitúan las medidas de las alturas de los centros B, C y D.
13 – Por cada centro se traza una línea horizontal (en el espacio sería un plano horizontal) hasta tocar a la curva y esto nos da los radios correctos (las horizontales de la izquierda).
Vértices del hueco pentagonal en las vistas.
14 – Para dibujar el hueco pentagonal en el perfil desde sus centros B, C y D en el alzado se dibujan horizontales hacia el perfil.
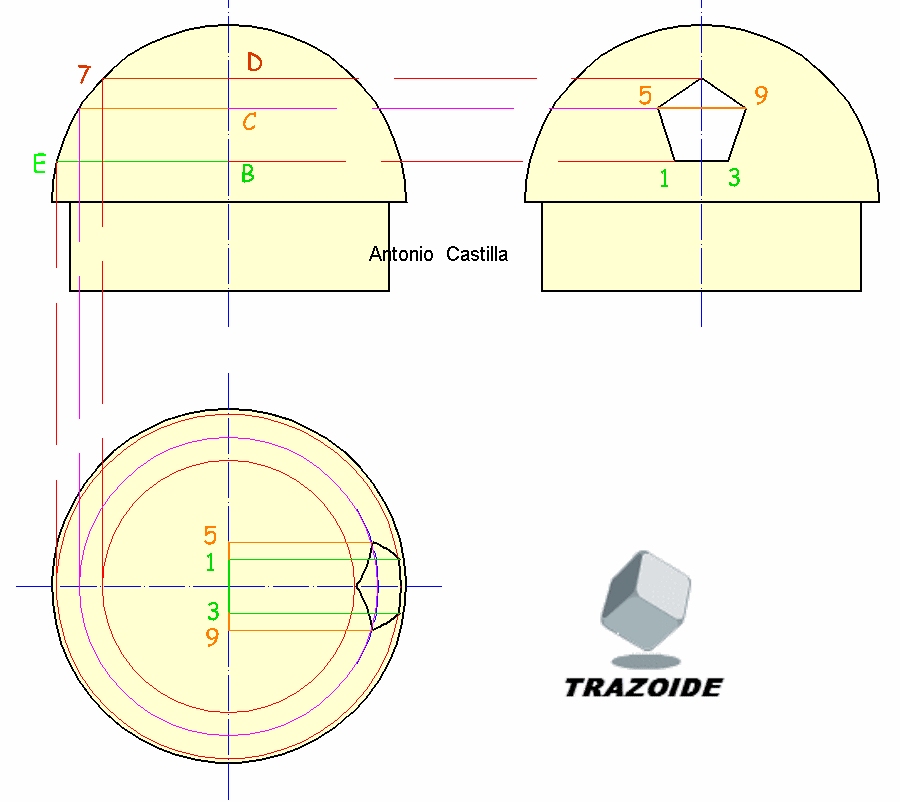
15 – En la perspectiva se miden las cuerdas 1-3 y 5-9 que están en verdadera magnitud por ser su unión paralelas al eje X. En el perfil a partir del eje se llevan la mitad de esas cuerdas y con ello tenemos los puntos del pentágono. Las uniones de los puntos son líneas rectas.
16 – En la planta también se han llevado las cuerdas 1-3 y 5-9 colocándolas sobre el eje vertical y desplazándolas hacia un lado y estando sobre las circunferencias que se obtuvieron en el alzado. Las uniones de los puntos son curvas (arcos de elipses).
Ejes de las elipses del hueco pentagonal en la planta.
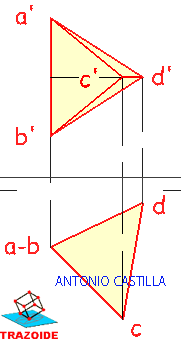
17 – Plantearé solo uno, los demás se hacen igual. En el perfil vemos los planos del hueco pentagonal como planos proyectantes (se ven como una línea). Se trata de hallar la sección de un esfera por un plano. Si prolongamos el plano hasta cortar a la esfera obtenemos la media del eje mayor, q, de la sección.
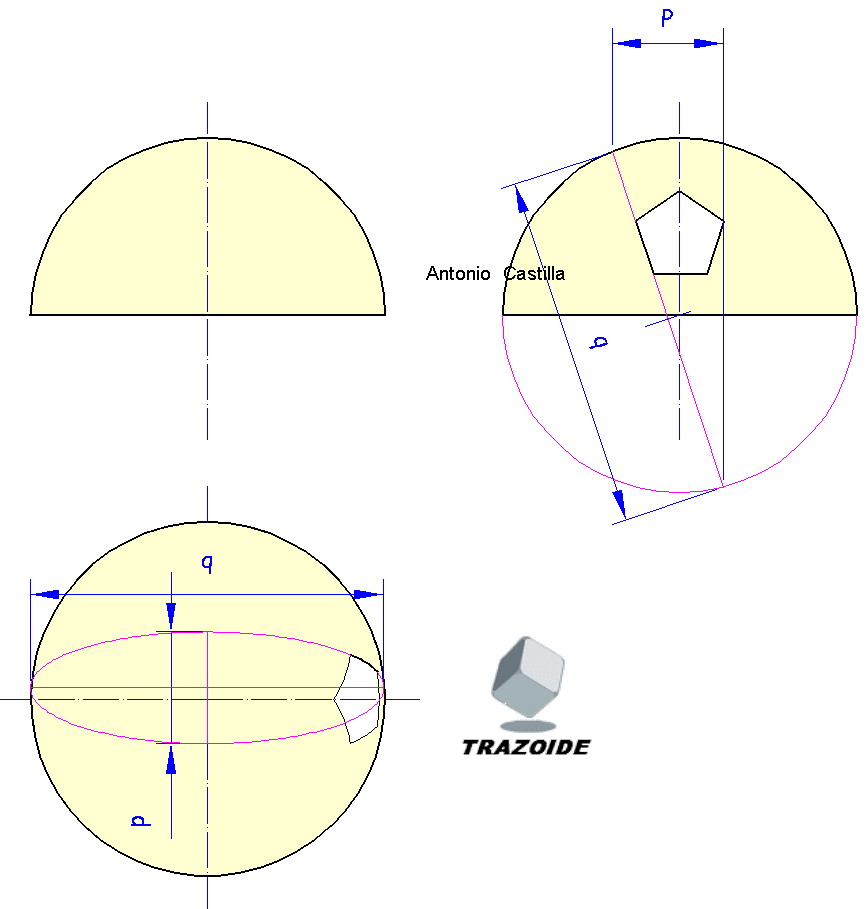
18 – Su centro se localiza en su punto medio y este se lleva a la planta, así como el eje mayor, q.
19 – En el perfil la proyección horizontal, p, del plano es el eje menor de la elipse. Llevarla a la planta en perpendicular al eje mayor.
20 – Se realizaría lo mismo para los otros planos. El plano del lado inferior del pentágono no produce una elipse en la planta sino una circunferencia. La intersección de todas las elipses es el hueco pentagonal.
Puntos de las elipses del hueco pentagonal en la planta.
21 – Para obtener puntos para el trazado de las elipses de los huecos pentagonales se puede recurrir a cualquier procedimiento para su obtención a partir de los ejes principales o mediante métodos propios del diédrico. Hallaré un punto de está forma. En el perfil determino un punto r» que deseo llevar a la planta.
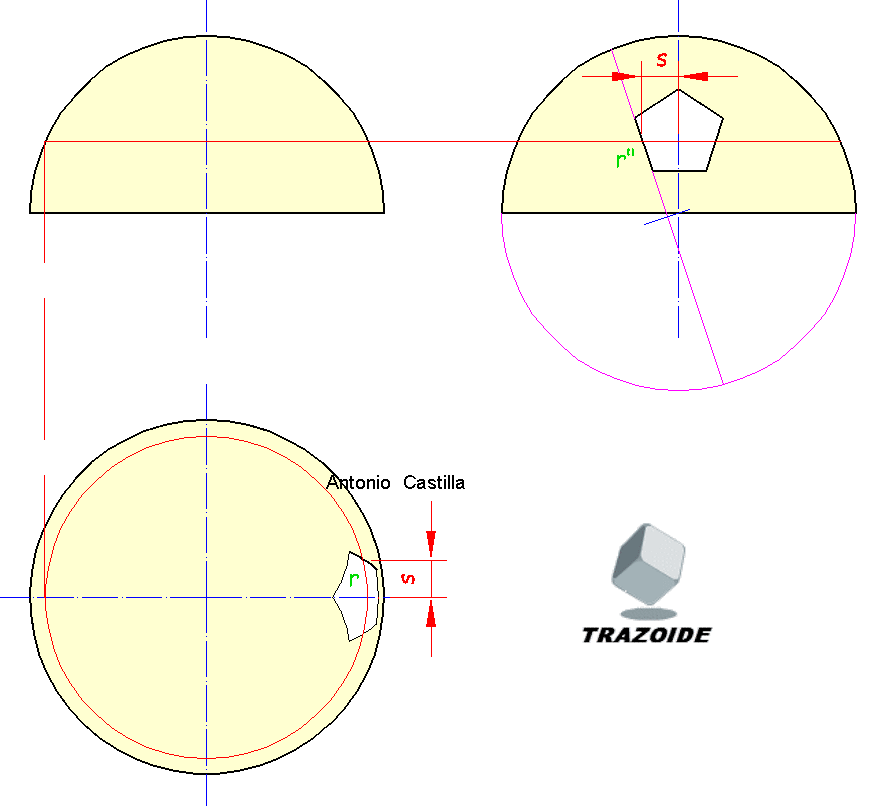
22 – Se mide su proyección horizontal, s, y se lleva a la planta sobre una circunferencia que se ha obtenido por el plano horizontal que pasa por él desde el alzado llevándola a la planta.
23 – Repetir con más puntos y unirlos a mano alzada.
Vistas completas.
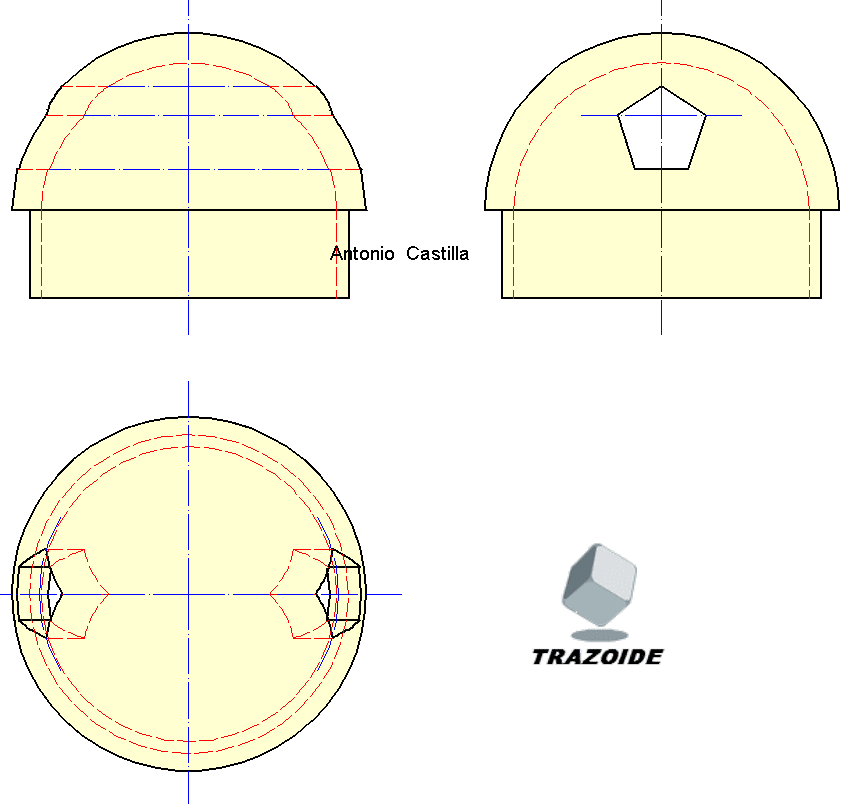
24 – Las vistas completas son estas :
Inicio > Sistema diédrico > Intersecciones de cuerpos en diédrico | |






Intersección – 981