Mes: octubre 2014

Ejercicios resueltos de enlaces y tangencias – 112

Inicio > Geometría plana > Enlaces y tangencias

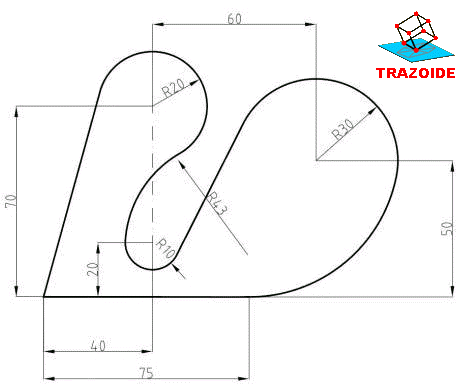
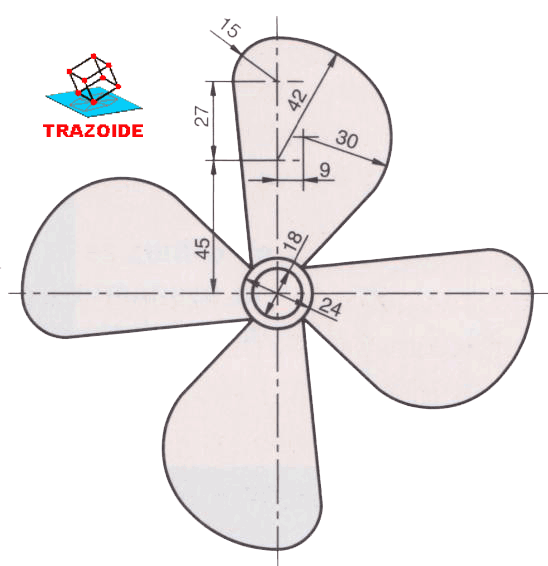
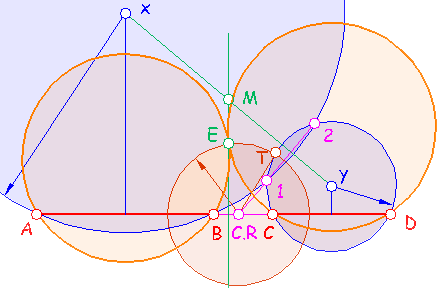
En la imagen se muestra el extremo abombado de un eje formada por arcos de circunferencias. Dibujarlo determinando los centros y puntos de tangencia.

---

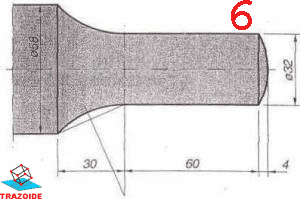
SOLUCIÓN

1 – Dibujamos una línea horizontal, el eje.
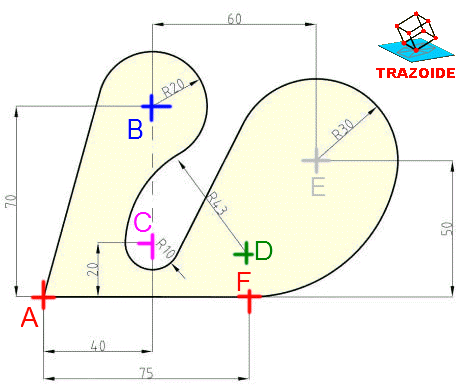
2 – Empezando por el lado izquierdo, en perpendicular al eje se traza una segmento que mida 58/2 hacia ambos lados, punto C de la siguiente imagen.

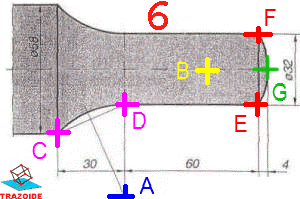
3 – Sobre el eje y desde la línea anterior dibujamos otra perpendicular al eje separada 30 mm de la anterior, y hacia cada lado marcamos 32/2, punto D.
4 – Unir los dos puntos C y D y trazar su mediatriz. Donde esta corte a la prolongación de la perpendicular que pasa por D es el centro A.
5 – Desde la perpendicular que pasa por D dibujar otra separada 60 mm hacia la derecha y medir hacia ambos lados una medida de 32/2, puntos E y F.
6 – Sobre el eje y a partir de la línea anterior medir 4 mm hacia la derecha, punto G.
7 – Unir el punto G con E y F. Hallar las mediatrices de EG y FG y donde se corten es el centro B del extremo derecho. Si se quiere no es necesario hallar las dos mediatrices con solo una de las dos donde corte al eje se obtiene B.

---

Inicio > Geometría plana > Enlaces y tangencias | | Vídeos sobre enlaces y tangencias

Ejercicios resueltos de enlaces y tangencias – 111

Inicio > Geometría plana > Enlaces y tangencias

En la imagen se muestra un alga formada por arcos de circunferencias. Dibujarla determinando los centros y puntos de tangencia.

---

SOLUCIÓN

1 – Situar el punto A y desde él medir 40 hacia la derecha y 70 hacia arriba y tenemos el centro B. Con radio 20 dibujar una circunferencia.

2 – Desde el punto A trazar la recta tangente exterior a la circunferencia de centro B.
3 – Desde el punto A medir 40 hacia la derecha y 20 hacia arriba y tenemos el centro C. Con radio 10 dibujar una circunferencia.
4 – Con centro en B y radio 20 + 43 trazar un arco. Con centro en C y radio 43 – 10 se dibuja otro arco. Donde se corten los dos arcos es el centro D. Con radio 43 dibujar un arco que enlace a los otros dos.
5 – A partir de A medir 75 hacia la derecha y tenemos el punto F.
6 – Desde el punto B hacer una línea vertical a 60 mm hacia la derecha. Desde la recta AF dibujar una recta horizontal separada 50 mm hacia arriba. Donde se encuentren las dos líneas es el centro E. Con radio 30 dibujar una circunferencia.
7 – Dibujar la tangente interior entre las circunferencias de centros C y E.
8 – Desde el punto F levantar uan recta perpendicular a AF. Desde E dibujar una horizontal. Donde ambas se corten es el centro del arco inferior derecho, dibujarlo.

---

Inicio > Geometría plana > Enlaces y tangencias | | Vídeos sobre enlaces y tangencias

Ejercicios resueltos de enlaces y tangencias – 110

Inicio > Geometría plana > Enlaces y tangencias

Circunferencias tangentes a una recta R, con sus centros en otra recta S y que pasen por un punto de dicha recta, P.

---

SOLUCIÓN

1 – Desde el punto dado, P, se levanta una perpendicular a la recta que contiene a los centros, S.

2 – Se halla la bisectriz entre la perpendicular y la recta a la que serán tangentes, R. Como ambas rectas forman dos ángulos existen dos posibles bisectrices y por tanto dos soluciones.
3 – Donde las bisectrices corten a la recta que contiene a los centros, S, son los centros de las circunferencias buscadas, C1 y C2.
4 – Desde los centros, C1 y C2, se trazan perpendiculares a la recta tangente, R, y los pies son los puntos de tangencia, T1 y T2.
5 – Dibujar las circunferencias con los centros hallados, C1 y C2, y radio hasta el punto dado P o hasta los puntos de tangencia, T1 y T2.

---

Inicio > Geometría plana > Enlaces y tangencias | | Vídeos sobre enlaces y tangencias

Inicio > Geometría plana > Enlaces y tangencias

Reproducir la figura, hélice de barco o ventilador, indicando claramente los centros y puntos de tangencia de los diferentes arcos de enlaces.

---

SOLUCIÓN

1 – Colocar el primer centro, A, y las circunferencias centrales de diámetro 18 y 24 mm.

2 – Trazar un eje vertical por A y sobre él medir 45 mm para situar el centro B.

3 – Subir 27 mm más para situar C.

4 – Con centro en C y radio 15 mm se traza el arco superior izquierdo.

5 – Con centro en B y radio 42 mm se traza el arco superior derecho.

6 – Se dibuja una paralela al eje vertical separada 9 mm hacia la derecha. Con centro en B y radio 42 – 30 = 12 mm se traza un arco. Donde el arco corte a la paralela es el centro D.

7 – Con centro en D y radio 30 trazar el arco lateral derecho.

8 – Para el lado izquierdo trazar la tangente exterior entre la circunferencia de centro A y diámetro 18 y la de centro C y radio 15.

9 – Para el lado derecho dibujar la tangente a la circunferencia de centro D y radio 30 respecto de un punto, el centro A.

 

---

Inicio > Geometría plana > Enlaces y tangencias | | Vídeos sobre enlaces y tangencias

 

Ejercicios de enlaces y tangencias – 108

Inicio > Geometría plana > Enlaces y tangencias

En una chapa se realizan dos agujeros de diámetros 60 y 40 mm, con distancia entre ambos de 70 mm. Obtener los diámetros de dos bolas iguales que encajen en los referidos taladros y que sean tangentes entre sí.
Otra ora de expresar el mismo enunciado :
Circunferencias de igual radio, tangentes entre sí, conocidas dos cuerdas, AB y CD

---

SOLUCIÓN

1 – Trazar las mediatrices de AB y CD

2 – Con centro en cualquier punto de ellas, X e Y, y radio hasta los extremos de los segmentos, AB y CD, trazar dos circunferencias que se corten entre sí
3 – Unir los puntos de corte de las dos circunferencias, 1 y 2, y prolongarlo hasta que corte a los segmentos AB y CD (punto C.R)
4 – Hallar la tangente a una de las dos circunferencias auxiliares, X o Y, que parte de C.R. El punto de tangencia es T
5 – Con centro en C.R y radio hasta T hacer una circunferencia
6 – Unir X con Y y por su punto medio dibujar una perpendicular a AB o CD (también se puede trazar la perpendicular a AB por el punto medio de la distancia entre los puntos medios de AB y CD)
7 – Donde esta última perpendicular corte a la circunferencia de centro C.R es el punto E, punto de tangencia de las dos circunferencias solución
8 – Hacer una circunferencia que pase por A, B y E y otra por C, D y E. Ambas son las soluciones buscadas

---

Inicio > Geometría plana > Enlaces y tangencias | | Vídeos sobre enlaces y tangencias

Ejercicios de enlaces y tangencias – 107

Inicio > Geometría plana > Enlaces y tangencias

Dibujar tres circunferencias tangentes interiormente a un triángulo isósceles, ABC, cada una a dos lados del triángulo y tangentes entre sí exteriormente.

---

SOLUCIÓN

1 – Hallar la bisectriz de uno de los ángulos, A por ejemplo, y hacer una circunferencia, centro 1′, de radio cualquiera tangente a dos lados

2 – Trazar otra igual tangente a ella y a un mismo lado, la de centro 2′
3 – Hallar una tercera circunferencia, 3′, tangente a las dos anteriores, 1′ y 2′, y a uno de los lados, AC (esto lo explico en el siguiente mensaje)
4 – Hacer una recta, B’C’, paralela al lado BC y tangente a las circunferencias 2′ y 3′
5 – Unir 1′ con B’ y después una paralela a ella por B. Donde corte a la bisectriz de A es el centro de la circunferencia buscada, 1, su radio mediante una perpendicular a AB por 1.
6 – Hacer otra igual, centro 2, tangente a la primera
7 – Unir el centro 1′ con 3′ y trazar una paralela por 1 hasta cortar a la bisectriz de C. Este será el centro 3 de la tercera circunferencia, de radio hasta donde la unión de 1 con 3 corta a la circunferencia de 1

---

Inicio > Geometría plana > Enlaces y tangencias | | Vídeos sobre enlaces y tangencias

Ejercicios de enlaces y tangencias – 106

Inicio > Geometría plana > Enlaces y tangencias

Hallar dos circunferencias iguales tangentes entre sí, además de ser tangente cada una a un lado distinto de un triángulo conocido y tangentes ambas al tercer lado.

---

SOLUCIÓN

1 – Se traza una circunferencia de radio cualquiera tangente a dos lados (la de centro x’), y otra de igual radio tangente a ella y al mismo lado

2 – Trazar una tangente al lado BC por la segunda circunferencia (lado B’C’)
3 – Unir el vértice A con el centro X’, y este a su vez con B’
4 – Por el vértice B se hace una paralela a B’X’
5 – Donde esta última corte a AX’ es el centro de la circunferencia buscada, X
6 – Por X se hace una perpendicular a AB y ese es el radio de la circunferencia buscada
7 – Trazar la otra

---

Inicio > Geometría plana > Enlaces y tangencias | | Vídeos sobre enlaces y tangencias

Inicio > Geometría plana > Enlaces y tangencias

Construir tres circunferencias tangentes entre sí y que sus respectivos centros sean los vértices del triángulo de 90, 60 y 80 mm.

---

SOLUCIÓN

1 – Halla el incentro (punto de corte de las tres bisectrices del triángulo).

2 – Desde el incentro se trazan rectas perpendiculares a los lados del triángulo.

3 – Donde esas perpendiculares corte a los lados del triángulo son los puntos de tangencia de las circunferencias.

4 – Con centro en los vértices del triángulo y radio hasta los puntos de tangencia se dibujan las circunferencias pedidas.

---

Inicio > Geometría plana > Enlaces y tangencias | | Vídeos sobre enlaces y tangencias

 

Inicio > Geometría plana > Enlaces y tangencias

Dados tres puntos A, B y C no alineados, dibujar tres circunferencias tangentes dos a dos en dichos puntos. (AB = 3,5 cm BC = 4,5 cm Y CA = 4 cm)

---

SOLUCIÓN

1 – Halla el circuncentro (punto de corte de las mediatrices) del triángulo formado con los tres puntos.

2 – Une el circuncentro con los tres puntos.

3 – Traza líneas perpendiculares a esa últimas por los tres puntos.

4 – Prolongarlas hasta formar un nuevo triángulo.

5 – Los vértices de este nuevo triángulo son los tres centros de las circunferencias buscadas. El radio es hasta los puntos dados.

---

Inicio > Geometría plana > Enlaces y tangencias | | Vídeos sobre enlaces y tangencias

 

Ejercicios resueltos de enlaces y tangencias – 103

Inicio > Geometría plana > Enlaces y tangencias

Conocido un triángulo rectángulo ABC, dibujar dos circunferencias del mismo radio y tangentes entre sí tal que:
– Una tiene centro en el vértice C
– Otra tiene centro en el lado CB y además es tangente al lado AB

---

SOLUCIÓN

1 – Con centro en C y un radio cualquiera, trazar una circunferencia (azul)

2 – Dibujar otra igual tangente a ella y con centro en BC
3 – Tangente a esta última haces una paralela a AB
4 – Unir A’ con T’ (punto de tangencia de las dos circunferencias auxiliares), o cualquier otro punto que quieras averiguar como el centro de la circunferencia
5 – Hacer una paralela a A’T’ por A y donde corte a BC es T punto de tangencia de las circunferencias buscadas
6 – Con centro en C y radio hasta T se traza la primera circunferencia.

---

Inicio > Geometría plana > Enlaces y tangencias | | Vídeos sobre enlaces y tangencias