Categoría: Uncategorized

Figuras idénticas, dos figuras son idénticas cuando superpuestas coinciden todos sus puntos.

No se debe confundir figuras idénticas con figuras iguales. Así dos figuras son iguales si todos sus elementos son los mismos pero no pueden superponerse, como en la simetría axial, mientras que si esto es posible son idénticas.

Por lo tanto dos figuras idénticas son iguales, pero dos figuras iguales no son idénticas. La identidad se suele representar con tres trazos horizontales, mientras la igualdad por dos.

Inicio > Sistema diédrico > Intersecciones planas en diédrico

Intersección entre varios planos

1. Poliedro formado por la intersección entre tres planos y los planos de proyección
2. Poliedro formado por la intersección entre cuatro planos y los planos de proyección
3. Intersección entre un plano definido por un paralelogramo y cuatro planos definidos por cuadrados
4. Cubierta de planta hexagonal

 

---

Inicio > Sistema diédrico > Intersecciones planas en diédrico | | Vídeos sobre intersecciones en diédrico

 

Inicio > Sistema diédrico > Intersecciones planas en diédrico

Intersección entre tres planos

1. Intersección de tres planos (uno oblicuo, otro frontal y otro paralelo a la línea de tierra)
2. Intersección de tres planos (uno oblicuo, otro horizontal y otro paralelo a la línea de tierra)

---

Inicio > Sistema diédrico > Intersecciones planas en diédrico | | Vídeos sobre intersecciones en diédrico

 

Inicio > Sistema diédrico > Intersecciones planas en diédrico

Vídeos de intersección entre dos planos

1. Intersección de dos triángulos. Selectividad Aragón 2015
2. Vídeos de intersección entre dos planos

Intersección entre dos planos

– Dos planos oblicuos, conocidas sus trazas

1. Intersección de dos planos, conocidas sus trazas
2. Intersección entre dos planos con el mismo vértice
3. Intersección entre dos planos cuyas trazas verticales coinciden con las horizontales y viceversa
4. Intersección entre dos planos oblicuos cuyas trazas se cortan fuera de los límites del papel
5. Intersección entre dos planos oblicuos cuyas trazas horizontales son paralelas entre sí

– Dos planos oblicuos, sin conocer sus trazas

1. Intersección entre dos planos definidos por tres puntos
2. Intersección de dos planos definidos por tres puntos
3. Intersección entre dos triángulos (planos definidos por tres puntos), uno de ellos proyectante
4. Intersección entre dos triángulos (planos definidos por tres puntos)
5. Intersección entre dos planos, uno dado por dos rectas y otro por su recta de máxima pendiente
6. Intersección de dos planos paralelos a la línea de tierra (definidos por cuatro puntos) sin utilizar el perfil
7. Intersección entre dos triángulos (planos definidos por tres puntos)
8. Intersección de un plano que pasa por la línea de tierra y un plano dado por dos rectas
9. Prolongar una casa hasta una cochera manteniendo la inclinación de las cubiertas (Intersección de dos planos)

– Un plano oblicuo y otro de perfil

1. Intersección de un plano oblicuo con uno de perfil

– Un plano oblicuo y otro frontal

1. Intersección entre un plano oblicuo y uno frontal

– Un plano cualquiera y un bisector

1. Intersección entre un plano y los bisectores

– Un plano de canto (proyectante vertical) y un plano frontal

1. Intersección entre un plano frontal y uno proyectante vertical (de canto)

– Un plano oblicuo y uno perpendicular al segundo bisector

1. Intersección entre un plano que pasa por línea de tierra y uno perpendicular al segundo bisector

– Un plano oblicuo y uno que pasa por la línea de tierra

1. Intersección entre un plano general y uno que pasa por línea de tierra (sin utilizar el perfil)
2. Intersección entre un plano general y uno que pasa por línea de tierra (utilizando el perfil)
3. Intersección entre un plano que pasa por línea de tierra y uno oblicuo (o general)
4. Intersección entre un plano que pasa por línea de tierra y uno perpendicular al segundo bisector

– Dos planos paralelos a la línea de tierra

1. Intersección de dos planos paralelos a la línea de tierra (definidos por cuatro puntos) sin utilizar el perfil
2. Intersección de dos planos paralelos a la línea de tierra

– Uno oblicuo y otro proyectante

1. Intersección entre dos triángulos (planos definidos por tres puntos), uno de ellos proyectante

– Uno paralelo al primer bisector y otro perpendicular al segundo bisector

1. Intersección entre un plano que paralelo al primer bisector y uno perpendicular al segundo bisector (o intersección entre dos planos perpendiculares al segundo bisector)

– Dos perpendiculares al segundo bisector

1. Intersección entre dos planos perpendiculares al segundo bisector (o intersección entre un plano que paralelo al primer bisector y uno perpendicular al segundo bisector)

---

Inicio > Sistema diédrico > Intersecciones planas en diédrico | | Vídeos sobre intersecciones en diédrico

 

Recta y circunferencia disjunta, son las que no tienen ningún punto en común, también se les denomina no secantes.

El término contrario es incidente o secante, es decir, cuando sí se cortan.

Inicio > Sistema axonométrico > Isométrica ||
Algunas personas se quedan con la duda de colocar o no determinadas aristas sobre una cara, sin tener claro si existen o no.

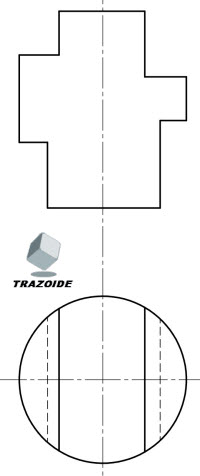
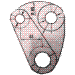
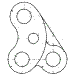
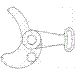
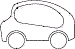
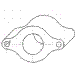
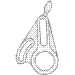
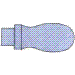
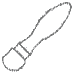
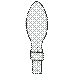
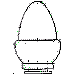
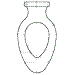
Por ejemplo, en la perspectiva isométrica planteada para estas tres vistas :

---

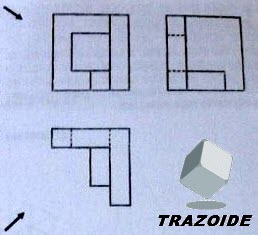
SOLUCIÓN

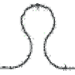
Una solución propuesta muy habitual es esta :

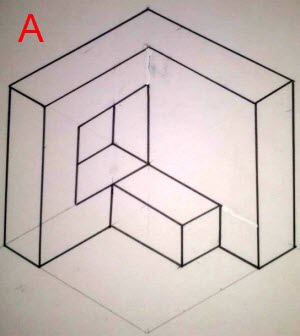
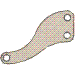
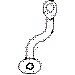
A esa solución le falta la línea gruesa naranja y le sobran las líneas gruesas amarilla y azul.

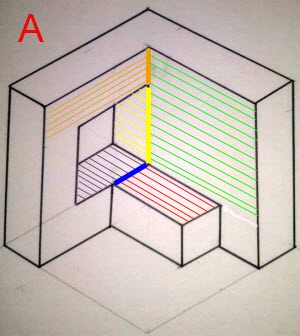
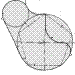
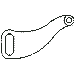
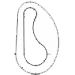
A veces es útil visualizar los planos que forman las caras dibujando líneas paralelas, que para mí son como la huella que va dejando el dedo (o lo que se siente) al deslizarlo por la pieza.

Dibujamos una línea donde hay una arista, es decir, la intersección de dos planos.

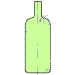
La línea gruesa naranja es la intersección (rincón) entre el plano formado por las líneas finas naranjas y verdes.
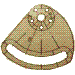
Sin embargo, la línea gruesa amarilla sobra porque los planos formados por las líneas finas verdes y amarillas están unas a continuación de otras por lo que no hay ninguna arista entre ellas.

Lo mismo ocurre con las líneas finas rojas y azules, forman un único plano y no dos, por lo que no hay ninguna línea de separación entre ellas (la línea gruesa azul, que se debe quitar).

---

Inicio > Sistema axonométrico > Isométrica

    

isometrica-919

La teoría sobre las relaciones de los ángulos de una circunferencia es muy útil para realizar demostraciones o resolver problemas de todo tipo desde construcción de polígonos (en especial los inscritos y circunscritos) hasta problemas de potencia o de tangencias, por lo que no se debe subestimar el conocimiento de dichas relaciones y sí es aconsejable tener siempre un resumen de estas relaciones a mano.

Otros enlaces relacionados :

• Vídeos sobre trazados fundamentales o básicos en dibujo técnico
• Ejercicios sobre trazados fundamentales o básicos en dibujo técnico

Estás en : Geometría plana > Circunferencias

Inicio > Normalización > Vistas

Conocidas la planta y el alzado de un cuerpo cilíndrico con rebajes, se pide representar el perfil derecho, además de representar en croquis una vista axonométrica del objeto.

---

SOLUCIÓN

Esta es una imagen dinámica que da una idea clara de su forma :

 

Y estas son una imágenes estáticas :

---

Inicio > Normalización > Vistas | |

 

     

Inicio > Sistema diédrico > Icosaedros

 

Vídeos sobre icosaedros

1. Desarrollo de un icosaedro
2. Vídeo sobre partes vistas y ocultas en diédrico (visibilidad) 1ª parte
3. Vídeo sobre partes vistas y ocultas en diédrico (visibilidad) 2ª parte

 

Inicio > Sistema diédrico > Icosaedros | |

 

    

Inicio > Geometría plana > Enlaces y tangencias

 

Vídeos sobre enlaces y tangencias

1. Vídeos sobre enlaces y tangencias
2. Vídeos sobre enlaces de rectas
3. Vídeos sobre circunferencias tangentes conociendo el radio
4. Vídeos sobre circunferencias tangentes desconociendo el radio y el centro

 

Ejercicios de enlaces y tangencias

1. Ejercicio 1 (Compás de espesores)
2. Ejercicio 2 (Polea)
3. Ejercicio 3 (Remate)
4. Ejercicio 4 (Pez)
5. Ejercicio 5 (Llave fija)
6. Ejercicio 6 (Llave fija)
7. Ejercicio 7 (Silla de ruedas)
8. Ejercicio 8 (Ventanal)
9. Ejercicio 9 (Cortador)
10. Ejercicio 10 (Grifo)
11. Ejercicio 11 (Letra «a» minúscula – Selectividad Valencia 2010)
12. Ejercicio 12 (Biela)
13. Ejercicio 13 (Balancín)
14. Ejercicio 14 (Balancín)
15. Ejercicio 15 (Balancín, Selectividad 2007 junio Valencia)
16. Ejercicio 16 (Balancín)
17. Ejercicio 17 (Jarrón)
18. Ejercicio 18 (Alfil)
19. Ejercicio 19 (Alfil)
20. Ejercicio 20 (Troquel)
21. Ejercicio 21
22. Ejercicio 22 (Con un pentágono)
23. Ejercicio 23 (Con una elipse)
24. Ejercicio 24 (Coche)
25. Ejercicio 25 (Lira)
26. Ejercicio 26 (Botella)
27. Ejercicio 27 (Cuchara)
28. Ejercicio 29 (Corredera)
29. Ejercicio 30 (Separador)
30. Ejercicio 31 (Enlace de varios puntos)
31. Ejercicio 32 (Soporte curvo)
32. Ejercicio 33 (Ménsula)
33. Ejercicio 34 (Caballo)
34. Ejercicio 35 (Contrapeso)
35. Ejercicio 36 (Tirador)
36. Ejercicio 37 (Lira)
37. Ejercicio 38 (Puño)
38. Ejercicio 39 (Puño de manivela)
39. Ejercicio 40 (Puño)
40. Ejercicio 46 (Pestillo)
41. Ejercicio 47 (Pestillo)
42. Ejercicio 48 (Pestillo)
43. Ejercicio 49 (Terminal con ovoide)
44. Ejercicio 50 (Eslabón con ovoide / prueba de acceso a grado superior 2008)
45. Ejercicio 51 (Biela curva con óvalo y ovoide)
46. Ejercicio 52 (Selectividad Navarra 2008 / mosquetón con óvalo)
47. Ejercicio 53 (Junta – Selectividad Valencia 2010)
48. Ejercicio 54 (Junta)
49. Ejercicio 55 (Junta)
50. Ejercicio 56 (Junta)
51. Ejercicio 57 (Nudo de carreteras)
52. Ejercicio 58 (Selectividad Navarra 2008)
53. Ejercicio 59 (Hélice)
54. Ejercicio 60 (Paletas de ventilador)
55. Ejercicio 61 (Extremo de eje)
56. Ejercicio 62 (Jarrón)
57. Ejercicio 63
58. Ejercicio 64
59. Ejercicio 65 (Gancho)
60. Ejercicio 66 (Gancho)
61. Ejercicio 67 (Gancho)
62. Ejercicio 68 (Gancho)
63. Ejercicio 69 (Gancho)
64. Ejercicio 70 (Gancho)
65. Ejercicio 71 (Selectividad Valencia Junio 2008)
66. Ejercicio 72 (Enlace con parábola)
67. Ejercicio 73 (Enlace con elipse)
68. Ejercicio 74 (Engranaje para cadena)
69. Ejercicio 75 (Selectividad Valencia Rueda de bloqueo)
70. Ejercicio 76 (Guitarra eléctrica)
71. Ejercicio 77
72. Ejercicio 78
73. Ejercicio 79
74. Ejercicio 80
75. Ejercicio 81
76. Ejercicio 82 (Alga)

 

Rectas tangentes a circunferencias

1. Rectas tangentes a una circunferencia por un punto exterior
2. Recta tangente a una circunferencia por un punto de ella, si el centro de la circunferencia es inaccesible
3. Rectas tangentes exteriores a dos circunferencias
4. Rectas tangentes interiores a dos circunferencias
5. Rectas tangentes a una circunferencia y que disten una distancia de un punto dado

 

Enlaces de rectas o puntos mediante arcos

1. Enlazar dos rectas oblicuas con un arco de radio conocido
2. Enlazar dos rectas paralelas mediante dos arcos del mismo sentido
3. Enlazar dos rectas paralelas mediante dos arcos del mismo radio conocidos los puntos de tangencia
4. Enlazar mediante arcos varios puntos alineados
5. Enlazar varios puntos no alineados, con arcos de circunferencia, conocido el radio de primer enlace
6. Enlazar dos rectas paralelas con tres arcos (Selectividad Cataluña 2004)
7. Enlazar una recta y una circunferencia por dos arcos de igual radio

 

Tangencias de circunferencias conocido el radio

Una circunferencia y una recta

1. Circunferencia tangente a una recta y a una circunferencia conocido el radio
2. Circunferencia de radio conocido tangente a otra dada y a una recta

 

Una recta

1. Circunferencia de radio conocido tangente a una recta y que corta a otra recta según una cuerda de longitud conocida (Selectividad Madrid 2012)

Una circunferencia y un punto

1. Circunferencias tangentes a una circunferencia y que pasen por un punto, conocido el radio
2. Circunferencias tangentes a una circunferencia y que pasen por un punto, conocido el radio
3. Circunferencias de radio conocido tangentes a una circunferencia dada conocido su punto de tangencia

 

Dos circunferencias

1. Circunferencias tangentes con otras dos de radio conocido (tres casos distintos)
2. Circunferencias tangentes a dos circunferencias, interior una de otra, con otra de radio conocido
3. Circunferencias tangentes a otras dos con radio conocido
4. Circunferencias tangentes interiores a otras dos interior una a la otra, con radio conocido

 

Una recta y un punto

1. Circunferencia tangente a una recta y que pase por un punto, conocido el radio
2. Circunferencia tangente a una recta y que pase por un punto, conocido el radio

 

Dos rectas

1. Circunferencias de radio conocido tangentes a dos rectas

 

Tangencias y enlaces con circunferencias de centro inaccesible

1. Recta tangente a una circunferencia o arco por un punto de ella, si el centro de la circunferencia es inaccesible
2. Justificación del procedimiento de la recta tangente a una circunferencia o arco por un punto de ella, si el centro de la circunferencia es inaccesible
3. Recta tangente a una circunferencia o arco por un punto exterior, si el centro de la circunferencia es inaccesible

 

Arcos arquitectónicos

1. Arco carpanel de siete centros

 

Tangencias de circunferencias desconociendo el radio ( problemas de Apolonio )

1. Cómo dibujar circunferencias tangentes utilizando potencia (vídeo)
2. Circunferencias tangentes a una recta y que pasa por dos puntos, utilizando potencia (vídeo)

Recta, Recta, Recta – RRR

1. Circunferencias tangentes a tres rectas, siendo dos de ellas paralelas – Caso RRR
2. Circunferencias tangentes a tres rectas – Caso RRR

 

Circunferencia, Punto, Punto – CPP

1. Circunferencias tangentes a otra y que pasa por dos puntos – Caso CPP / Mediante potencia
2. Circunferencias tangentes a un circunferencia y que pasen por dos puntos – Caso CPP / Mediante potencia e inversión
3. Circunferencias tangentes a otra y que pasa por dos puntos, simétricos respecto de un diámetro – Caso CPP / Mediante potencia
4. Circunferencias tangentes a otra y que pasa por dos puntos – Caso CPP / Mediante potencia
5. Circunferencias tangentes a otra y que pasen por dos puntos, uno de ellos sobre la circunferencia – Caso CPP
6. Hallar un punto en una recta que equidiste de un punto y de una circunferencia (Circunferencia tangente a una circunferencia y que pase por dos puntos) – Caso CPP
7. Circunferencias tangentes a otra y que pasen por dos puntos interiores a la circunferencia – Caso CPP / Mediante inversión

 

Recta, Recta, Circunferencia – RRC

1. Circunferencia tangente a las dos rectas y a otra circunferencia, también tangente a las rectas – Caso RRC / Mediante potencia
2. Hallar las circunferencias tangentes a dos lados de un triángulo y a la circunferencia inscrita a ese triángulo (Circunferencias tangentes a dos rectas y a una circunferencia) – Caso RRC / Mediante potencia
3. Circunferencias tangentes a dos rectas y una circunferencia – Caso RRC
4. Circunferencias tangentes a dos rectas y una circunferencia – Caso RRC
5. Circunferencias tangentes a dos rectas y una circunferencia, que forman un sector circular – Caso RRC
6. Circunferencias tangentes a dos rectas paralelas y una circunferencia – Caso RRC
7. Circunferencias tangentes a dos rectas y a una circunferencia que las atraviesa – Caso RRC / Mediante dilatación negativa
8. Circunferencias tangentes a dos rectas y a una circunferencia, conocidos los ángulos que forma la circunferencia buscada con las rectas – Caso RRC / Mediante dilatación negativa
9. Circunferencias tangentes a dos rectas y a una circunferencia que también es tangente a las dos rectas – Caso RRC / Mediante potencia y homotecia

 

Circunferencia, Recta, Punto – CRP

1. Circunferencias tangentes a una circunferencia, a una recta y que pasen por un punto de la recta – Caso CRP / Mediante potencia
2. Pestillo, Circunferencias tangentes a una circunferencia, a una recta y que pasen por un punto de la recta – Caso CRP / Mediante potencia
3. Circunferencias tangentes a una circunferencia, a una recta y que pasen por un punto de la recta – Caso CRP / Mediante potencia
4. Circunferencias tangentes a una circunferencia y a una recta conocido el punto de tangencia en la circunferencia – Caso CRP/ Mediante potencia
5. Circunferencias tangentes a una circunferencia, a una recta y que pasen por un punto exterior de la circunferencia – Caso CRP
6. Circunferencias tangentes a una circunferencia, a una recta y que pasen por un punto exterior de la circunferencia – Caso CRP
7. Circunferencias tangentes a una circunferencia, a una recta y que pasen por un punto interior de la circunferencia – Caso CRP
8. Circunferencias tangentes a una circunferencia, a una recta secante a la circunferencia y que pasen por un punto interior de la circunferencia – Caso CRP / Mediante inversión
9. Circunferencias tangentes a una circunferencia y a una recta conocido el punto de tangencia en la recta – Caso CRP / Mediante potencia
10. Circunferencias tangentes a una circunferencia y a una recta conocido el punto de tangencia en la recta – Caso CRP
11. Biela, con circunferencia tangente a una recta, a una circunferencia y que pase por un punto de ella – Caso CRP / Mediante potencia
12. Circunferencia tangente a una recta, a una circunferencia y que pase por un punto de ella – Caso CRP (selectividad Andalucía 2008)
13. Circunferencia tangente a una recta, a una circunferencia y que pase por un punto, conocido el ángulo que forma la circunferencia buscada con la recta – Caso CRP / Mediante inversión
14. Circunferencia tangente a una recta, a una circunferencia y que pase por un punto de la recta – Caso CRP / Mediante inversión
15. Circunferencia tangente a una recta, a una circunferencia y que pase por un punto de la recta – Caso CRP / Mediante inversión
16. Circunferencia tangente a una recta, a una circunferencia y que pase por un punto de la circunferencia – Caso CRP / Mediante inversión
17. Circunferencias tangentes a una circunferencia, a una recta y que pasen por un punto exterior a ellos – Caso CRP / Mediante potencia

 

Circunferencia, Circunferencia, Punto – CCP

1. Circunferencias tangentes a dos (una interior de la otra) y a un punto (interior a una de ellas – Caso CCP /Mediante inversión
2. Circunferencias tangentes a otras dos y que pasen por un punto – Caso CCP / Mediante inversión y/o potencia
3. Circunferencias tangentes a otras dos y que pasen por un punto – Caso CCP / Mediante inversión
4. Circunferencias tangentes a otras dos y que pase por un punto (remate) – Caso CCP / Mediante potencia
5. Circunferencias tangentes a otras dos y que pasen por un punto – Caso CCP / Mediante potencia
6. Circunferencias tangentes a otras dos y que pase por un punto – Caso CCP / Mediante inversión
7. Circunferencias tangentes a otras dos iguales y que pase por un punto interior a una de ellas – Caso CCP / Mediante inversión
8. Circunferencias tangentes a otras dos iguales y que pase por un punto interior a una de ellas – Caso CCP
9. Dadas dos circunferencias tangentes interiores hallar otra tangente a las dos dadas y que pase por el centro de una de ellas – Caso CCP / Mediante inversión)
10. Circunferencias tangentes a otras dos y que pase por un punto de una de ellas – Caso CCP
11. Circunferencias tangentes a dos circunferencias y que pasen por un punto perteneciente a una de ellas – Caso CCP / Mediante potencia
12. Circunferencias tangentes a otras dos y que pase por un punto de una de ellas – Caso CCP / Mediante potencia
13. Circunferencias tangentes a otras dos y que pase por un punto de una de ellas – Caso CCP / Mediante potencia
14. Circunferencias tangentes a otras dos y que pase por un punto de una de ellas – Caso CCP / Mediante potencia
15. Circunferencias tangentes a otras dos y que pase por un punto de una de ellas – Caso CCP / Mediante potencia
16. Circunferencias tangentes a otras dos y que pase por un punto de una de ellas – Caso CCP / Mediante dilataciones
17. Circunferencias tangentes a otras dos y que pase por un punto de una de ellas – Caso CCP
18. Circunferencias tangentes a otras dos y que pase por un punto de una de ellas – Caso CCP / Mediante inversión
19. Circunferencias tangentes a otras dos y que pase por un punto de una de ellas – Caso CCP / Mediante inversión
20. Circunferencias tangentes a otras dos secantes y que pase por un punto de una de ellas – Caso CCP
21. Circunferencias tangentes a otras y que pase por un punto de una de ellas – Caso CCP / Mediante inversión y/o potencia
22. Circunferencias tangentes a otras y que pase por un punto de una de ellas – Caso CCP / Mediante potencia
23. Circunferencias tangentes a otras dos, una interior a la otra, y que pasen por un punto de la exterior – Caso CCP / Mediante potencia
24. Circunferencias tangentes a otras dos, una interior a la otra, y que pasen por un punto de la exterior – Caso CCP / Mediante inversión
25. Circunferencias tangentes a otras dos, una interior a la otra, y que pasen por un punto de la interior – Caso CCP / Mediante potencia
26. Circunferencia tangente a dos circunferencias iguales y pasa por el punto medio de la recta que une los centros de las dadas – Caso CCP / Mediante potencia
27. Circunferencia tangente a dos circunferencias iguales y que pasan por un punto exterior (Rodillo de fricción) – Caso CCP

 

Recta, Punto, Punto – RPP

1. Circunferencias tangentes a una recta y que pasen por dos puntos – Caso RPP / Mediante inversión
2. Circunferencias tangentes a una recta y que pasen por dos puntos – Caso RPP / Mediante potencia
3. Circunferencias tangentes a una recta y que pasen por dos puntos, uno de ellos sobre la recta – Caso RPP
4. Punto de una recta desde los que se ven otros dos con un ángulo máximo (Punto de la trayectoria de un futbolista para chutar con un ángulo máximo) – Caso RPP
5. Punto de la banda de un campo de fútbol desde el que chutar a la portería con un ángulo máximo – Caso RPP

 

Recta, Recta, Punto – RRP

1. Circunferencias tangentes a dos rectas y que pasan por un punto – Caso RRP / Mediante potencia
2. Circunferencias tangentes a dos rectas y que pasen por un punto – Caso RRP / Mediante potencia
3. Circunferencias tangentes a dos rectas y que pasan por un punto – Caso RRP / Mediante inversión
4. Circunferencias tangentes a dos rectas y que pasan por un punto – Caso RRP / Mediante homotecia
5. Circunferencias tangentes a dos rectas y que pasan por un punto que está en una de ellas – Caso RRP
6. Circunferencias tangentes a dos rectas y que pasan por un punto que está en la bisectriz- Caso RRP / Mediante potencia
7. Circunferencia que pasa por el centro de un cuadrado y es tangente a dos lados – Caso RRP / Mediante potencia

 

Circunferencia, Circunferencia, Recta – CCR

1. Circunferencias tangentes a dos circunferencias y a una recta, siendo las dos circunferencias dadas y la recta tangentes entre sí – Caso CCR
2. Circunferencia tangente a dos circunferencias iguales y a una recta tangente a una de ellas – Caso CCR
3. Circunferencia tangente a dos circunferencias y a una recta – Caso CCR / Mediante inversión
4. Circunferencias tangentes a dos circunferencia iguales, a una recta y que pasen por un punto de la recta – Caso CCR / Mediante potencia
5. Circunferencia tangente a dos circunferencias iguales y a una recta – Caso CCR / Mediante inversión y potencia
6. Circunferencias tangentes a dos circunferencia iguales y a una recta que sea paralela a la unión de sus centros – Caso CCR
7. Circunferencias tangentes a dos circunferencia y a una recta, estando el centro de una de las circcunferencias sobre la recta – Caso CCR

 

Circunferencia, Circunferencia, Circunferencia – CCC

1. Circunferencias tangentes a tres circunferencias de igual radio – Caso CCC / Mediante dilatación
2. Circunferencias tangentes a tres circunferencias, las dos menores de igual radio – Caso CCC / Mediante potencia
3. Circunferencias tangentes a tres circunferencias de distinto radio – Caso CCC
4. Circunferencias tangentes a tres circunferencias, las dos menores de igual radio y simétricas respecto de un radio de la mayor – Caso CCC
5. Circunferencias tangentes a tres circunferencias, que son tangentes entre sí – Caso CCC / Mediante inversión
6. Circunferencias tangentes a tres circunferencias, dos de ellas iguales y tangentes entre sí y tangentes interiormente a la mayor – Caso CCC / Mediante inversión
7. Punto que equidista de las paredes de tres depósitos cilíndricos – Caso CCC
8. Tres circunferencias tangentes conocidos sus centros y el centro radical – Caso CCC

 

Otros casos

1. Circunferencia tangente a una dada, conocida otra circunferencia y el eje radical con la buscada
2. Dibujar varias circunferencias iguales, tangentes entre sí y a una circunferencia dada exteriormente
3. Dibujar varias circunferencias iguales, tangentes entre sí y a una circunferencia dada interiormente
4. Circunferencias tangentes interiormente a una circunferencia y a cuatro radios no regulares
5. Dos circunferencias iguales y tangentes entre sí, con centro en un vértice de un triángulo rectángulo, el otro centro en la hipotenusa y tangente a un cateto
6. Hallar tres circunferencias tangentes entre sí, conocidos los puntos de tangencia
7. Hallar tres circunferencias tangentes entre sí conocidos los tres centros
8. Trazar dos circunferencias tangentes a los lados de un triángulo
9. Enlazar varios puntos con arcos que sean tangentes
10. Tres circunferencias tangentes a los lados de un triángulo isósceles
11. Circunferencias de igual radio, tangentes entre sí, conocidas dos cuerdas (o esferas de igual radio, tangentes entre sí, conocidos dos agujeros de un mismo plano en los que se alojan)
12. Trazar tres circunferencias alineadas y tangentes dos de ellas a una semicircunferencia (Hallar tres tubos tangentes entre sí, alineados y tangentes a un túnel semicircular)
13. Trazar tres circunferencias alineadas y tangentes dos de ellas a un arco de circunferencia no semicircular (Hallar tres tubos tangentes entre sí, alineados, y tangentes a un túnel curvo)
14. Trazar tres circunferencias tangentes a los lados de un cuadrado y entre sí, siendo el radio de una doble que otra
15. Trazar tres circunferencias tangentes a los lados de un triángulo y entre sí, siendo el radio de dos de ellas iguales
16. Enlazar una recta y una circunferencia por dos arcos de igual radio
17. Circunferencia tangente a una parábola además de al eje siendo el foco su punto de tangencia
18. Circunferencia tangente a una recta y que corte a otras dos según dos ángulos dados
19. Tres circunferencias distintas que sean tangentes a los lados de un triángulo y se corten entre sí en un mismo punto
20. Circunferencia tangente a una elipse y una recta

 

 

Tangencias de circunferencias conocidos donde estarán los centros

1. Hallar un circunferencia conocido su centro, el eje radical de esa con otra y esa segunda circunferencia
2. Circunferencia tangente a otras dos conocida la recta en la que está el centro
3. Hallar tres circunferencias tangentes entre sí, conocidos sus tres centros
4. Hallar tres circunferencias tangentes entre sí conocidos los tres centros
5. Hallar tres circunferencias tangentes entre sí, conocidos los puntos de tangencia
6. Hallar tres circunferencias tangentes entre sí conocidos los tres centros
7. Circunferencias tangentes a un circunferencia y que pasen por un punto conocida la recta en la que están los centros
8. Circunferencias tangentes a un circunferencia y que pasen por un punto conocida la recta en la que están los centros
9. Circunferencias tangentes a dos circunferencias, conocida la recta en la que están los centros
10. Circunferencias tangentes a una circunferencia conocida la recta en la que está el centro y un punto por el que pasa que está en la recta
11. Hallar un punto en una recta que equidiste de un punto y de una circunferencia (Circunferencia tangente a una circunferencia y que pase por un punto y tenga su centro en una recta) – Caso CPP
12. Circunferencia tangente a una recta, que pase por un punto de ella y tenga su centro en otra recta
13. Circunferencia tangente a la hipotenusa de un triángulo rectángulo, que pase por el ángulo recto y tenga su centro en un cateto
14. Circunferencia tangentes a dos circunferencias iguales con su centro en una recta conocida

Inicio > Geometría plana > Enlaces y tangencias | | Vídeos sobre enlaces y tangencias