Categoría: Uncategorized

Inicio > Libros > Libros de geometría descriptiva

Diédrico directo Tomo II (Superficies, intersecciones, cad, sombras)

Vicente Giménez Peris

Año 2014-1-1 / El autor / ISBN : 978-84-616-8764-0

Reseña
Segundo tomo que trata, como indica su subtitulo, de las superficies, las intersecciones entre cuerpos, la aplicación del cad y las sombras. Sin duda la calidad a la que nos tiene acostumbrado su autor no nos decepcionará al proporcionar el complemento que faltaba al primer tomo.

Al igual que el primer tomo, todo él está planteado en el diédrico directo, así que, se convertirá en un tomo imprescindible en nuestra biblioteca, ya que «sube» de nivel y pasamos de los típicos textos, que se quedan en lo elemental (punto, recta y plano), para pasar a los «cuerpos«.
Valoración
Valoración : 10/10
En general, un altamente recomendable e imprescindible libro sobre diédrico directo que complementa a la primera parte.
Idioma : Español
Tamaño : 238 páginas / 205 x 295 mm.

---

Inicio > Libros > Libros de geometría descriptiva

Editor : Antonio Castilla

Ejercicio de conjuntos y despieces – 983

Inicio > Normalización > Conjuntos y despieces

Realizar el despiece del siguiente conjunto de un soporte para taladrado :

---

SOLUCIÓN

PIEZA 1
Es suficiente con una vista completada con un corte parcial para ver el agujero más su sección.

PIEZA 2
El alzado más una sección completan las vistas necesarias.

PIEZA 3
Es un pasador cilíndrico al que se le ha añadido una sección rebatida.

PIEZA 4
El alzado se ha representado con un semicorte además de una vista parcial para que se aprecien el número de agujeros que tiene.

PIEZA 5
Al ser una pieza de revolución es suficiente con un semicorte.

PIEZA 6
Se representa igual que la pieza 4. La vista parcial se ha reducido gracias a la simetría.

PIEZA 7
Como no posee ningún detalle especial y es de revolución basta con un semicorte.

DESCRIPCIÓN DEL MECANISMO
Esto es un soporte para taladrado de bridas.
La pieza 7 es el soporte que sirve de apoyo y centrado al resto.
La pieza 6 es la brida que se desea taladrar. Inicialmente no tiene los cuatro agujeros, en el dibujo está ya el proceso final con los cuatro agujeros hechos. Esta pieza se coloca sobre la pieza 7 que es la que la mantiene centrada.
La pieza 4 se coloca encima de la pieza 6 y es la que la presiona uniformemente para mantenerla fija durante el taladrado.
El tornillo 1 rosca en la pieza 7 y su cabeza, la pieza 2, presiona a la pieza 4 para mantener a la pieza 6 fija.
La pieza 2 es el accionamiento del tornillo 1. En su periferia tiene un moleteado paralelo para accionarlo a mano. Para sujertar la pieza 2 a la 1 ambas poseen un orificio transversal en el que se introduce el pasador 3.
La pieza 5 son cuatro piezas iguales, una por cada agujero. Son casquillos de centrado para guiar a la broca.

---

Inicio > Normalización > Conjuntos y despieces

Inicio > Geometría plana > Enlaces y tangencias

Dibujar N circunferencias (por ejemplo 3) tangentes interiores a una dada y entre sí.

---

SOLUCIÓN

1 – Dibujar la circunferencia dada, centro O y radio O-A.

2 – Dividir la circunferencia en un número de partes iguales al de circunferencias que se desean hacer. En el ejemplo, se ha dividido en tres partes, A, B y C. Unir cada división con el centro, OA, OB y OC.

3 – Hallar la bisectriz del ángulo formado por dos divisiones. En la figura, al ángulo AOB se le ha trazado la bisectriz OD.

4 – Por uno de los extremos del ángulo, A, se dibuja una tangente a la circunferencia (perpendicular al radio OA).

5 – Se dibuja la bisectriz del ángulo formado por la primera bisectriz, OD, y la tangente AD, dando D1.

6 – Donde esta última bisectriz corte a la división OA es el primer centro, 1.

7 – Con centro en O y radio hasta 1 trazar una circunferencia que ira cortando a los demás radios en los restantes centros, 2 y 3.

8 – Hacer las circunferencias buscadas con esos centros y radio OA.

---

Inicio > Geometría plana > Enlaces y tangencias | | Vídeos sobre enlaces y tangencias

enlaces – 101

Inicio > Geometría plana > Enlaces y tangencias

Dados un punto, una recta y una circunferencia, hallar las circunferencias cuyo centro se encuentra en la recta, son tangentes a la circunferencia y pasan por el punto.
Se dan dos circunferencias C1,C2 y una recta r. Trazar las circunferencias con centro sobre r y tangentes a C1 y C2.

---

SOLUCIÓN

Te dan la recta en la que debe estar el centro, y como sabes, en ella estará contenido un diámetro de la circunferencia buscada.
Los diámetros dividen a las circunferencias en dos partes iguales (simétricas), luego tienes el eje de simetría (la recta que contiene al centro), por lo que si haces el simétrico del punto dado respecto de esa recta tendrás un segundo punto de la circunferencia buscada.
El problema te ha quedado reducido a otro : trazar las circunferencias tangentes a la circunferencia dada y que pasen por dos puntos (el dado y su simétrico respecto de la recta que contiene a los centros).
Para resolverlo puedes utilizar dos procedimientos, potencia o inversión.

Por potencia su solución sería esta :

Y aunque una imagen vale más que mil palabras, ahí van algunas :
1 – Supón el ejercicio resuelto (las soluciones están en línea blanca gruesa). El punto P dado es de la circunferencia buscada y el centro debe estar sobre la recta R, si quisiéramos trazar una recta tangente se haría una perpendicular al radio que une el punto de tangencia deseado, P, con el centro, y esa es la recta R dada, luego al hacerle una perpendicular a R por el punto P se ha dibujado una recta tangente a la circunferencia buscada (en amarillo).
2 – Ahora recordemos una propiedad (esta es solo una hay otras) fundamental del centro radical de dos circunferencias : «el centro radical es el punto por el que pasan las tangentes a tres circunferencias que miden lo mismo». Se puede expresar de otras formas pero así está más claro lo que quiero hacer, y es buscar el centro radical, por que ya que tengo una tangente, si localizo otra que mide lo mismo respecto de la circunferencia dada A, tendré los puntos de tangencia de la solución con la dada.
3 – Para determinar el centro radical se dibujan dos ejes radicales y donde estos se corten es el centro radical. Como la circunferencia dada debe tener su centro sobre la recta R, buscaré una cualquiera con su centro en dicha recta R, que pase por P y que corte a la dada A (la que está en magenta). Así la recta que se hizo perpendicular a R por P ya es un eje radical entre la circunferencia buscada y la elegida al azar (por ser las dos tangentes en P).
4 – Se determina el otro eje radical (entre la elegida al azar y la dada A), simplemente uniendo los puntos de corte de ambas (en azul). Donde se corte con la anterior es el centro radical (marcado en rojo con C.R.).
5 – Si con centro en el centro radical (C.R.) y radio hasta el punto P hago un arco (línea fina roja) corta a la circunferencia dada en T1 y T2. Lo que he hecho ha sido localizar los puntos de tangencia de la circunferencia dada A que miden lo mismo que la tangente desde la circunferencia buscada.
También se podría hacer las tangentes (línea blanca fina discontinua) a la circunferencia dada A desde el centro radical (C.R), y se obtienen los puntos de tangencia T1 y T2 (cada uno es para una solución distinta).
6 – Los puntos obtenidos son los puntos de tangencia con la circunferencia dada, para hallar los centros de la solución basta con unirlos con el centro de la circunferencia dada.
Si se hace por inversión, se resolveria así :
1 – Se toma uno de los puntos como centro de inversión y la circunferencia dada como circunferencia doble.
2 – Se halla el inverso del otro punto.
3 – Se determinan las rectas tangentes a la circunferencia dada y que pasen por el punto inverso del punto.
4 – Se une los puntos de tangencia con el punto tomado como centro de inversión, y donde corten a la circunferencia dada son los puntos de tangencia de la circunferencia buscada.
5 – Se unen dichos puntos con el centro de la circunferencia dada y donde corten a la mediatriz resultante de la unión de los dos puntos dados, son los centros de las circunferencias buscadas.

---

Inicio > Geometría plana > Enlaces y tangencias | | Vídeos sobre enlaces y tangencias

Inicio > Geometría plana > Enlaces y tangencias

Reproducir la figura, indicando claramente los centros y puntos de tangencia de los diferentes arcos de enlaces. ( Troquel )

---

SOLUCIÓN

1 – Dibujar un eje horizontal y desde su extremo, A, hacia la derecha se mide 60 mm, consiguiendo el centro B del arco que pasa por A.

2 – Hacer una línea horizontal separada 70/2 = 35 mm del eje central, hacia arriba y hacia abajo.

3 – Trazar otra paralela 10 mm por debajo de esta última, o separada 35 – 10 respecto del eje central.

4 – Con centro en B y radio 60 – 10 hacer un arco que corte a la paralela anterior, en el que será el centro C.

5 – Dibujar una nueva paralela al eje separada 40/2 = 20 mm hacia ambos lados.

6 – Trazar una nueva paralela al eje horizontal a (35 – 20)/2 y una línea vertical separada del punto A una distancia de 40 mm. Donde ambas se encuentren es el punto de tangencia D .

7 – A partir de la paralela que se hizo a 35 mm se hace otra separada 10 mm. Trazar una más separada también 10 mm respecto de la línea que se hizo a 20 mm.

8 – Con centro en D y radio 10 mm se dibuja un arco que cortará a las dos paralelas anteriores en los puntos E y F, centros de los dos arcos que enlazan.

---

Inicio > Geometría plana > Enlaces y tangencias | | Vídeos sobre enlaces y tangencias

Ejercicios resueltos de ELIPSES – 995

Inicio > Geometría plana > Elipses

Elipse conocido un punto de ella, P, y el eje menor, CD

---

SOLUCIÓN

1 – Determina el punto medio del eje menor, O.

2 – Con centro en O y radio la mitad del eje menor trazar una circunferencia.

3 – Por el punto dado, P, levanta una perpendicular al eje menor, y donde corte a la circunferencia es P’.

4 – Hacer otra perpendicular al eje menor por O, dando el punto A’ en la circunferencia.

5 – Une A’ con P’ hasta cortar al eje menor, punto X.

6 – Unir X con P y donde corte a la perpendicular que se trazó por O es A.

7 – La distancia OA es el semieje mayor.

8 – Ya se conocen el eje mayor y el menor, a partir de ellos dibujar el resto de la elipse.

---

Inicio > Geometría plana > Elipses | | Vídeos sobre elipses

Inicio > Sistema diédrico > Distancias en diédrico

Un trípode descansa sobre un suelo horizontal.

Una de las patas mide 7 m, forma con el suelo un ángulo de 50º y es paralela al vertical de proyección. Las otras dos patas miden 6’5 m y 5’7 m respectivamente.
En proyección horizontal las tres patas figuran igualmente espaciadas con una separación de 120°.

Hallar las proyecciones del trípode.

---

SOLUCIÓN

1 – Colocar en proyección vertical la recta a’-b’ que forme 50º con la línea de tierra y longitud 7 m.

2 – Hacer la proyección horizontal, paralela a la línea de tierra, en cualquier alejamiento y simplemente bajando perpendiculares a la línea de tierra desde los extremos de la proyección vertical.

3 – Desde el extremo de A en la proyección horizontal hacer dos líneas que formen 120° respecto de a-b.

4 – En proyección vertical, con centro en a’ y radio la longitud de los otros dos segmentos, 6’5 y 7’5 m, se dibujan dos arcos.

5 – Donde estos dos arcos corten a la línea de tierra,d’1 y c’1, se bajan dos perpendiculares a la línea de tierra, hasta una paralela a la línea de tierra que parta del punto A (puntos c1 y d1).

6 – Con centro en la proyección horizontal de a y radios hasta c1 y d1 hacer dos arcos hasta cortar a las líneas que están separadas 120° (puntos c y d).

7 – Subir las proyecciones horizontales de c y d, hasta la línea de tierra y unir con A (estas proyecciones no las tengo dibujadas).

---

Inicio > Sistema diédrico > Distancias en diédrico | | Vídeos sobre distancias

distancias – 976

Inicio > Sistema diédrico > Desarrollos

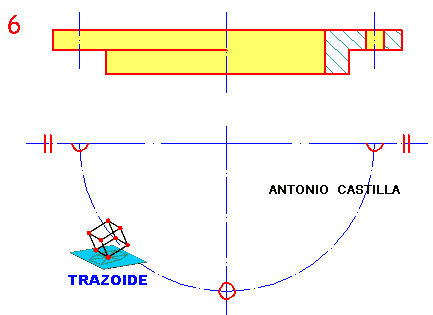
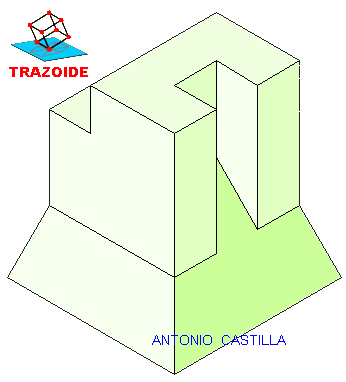
Tenemos un hexágono regular de centro O(20, 60, 0) situado en el plano horizontal y lados paralelos a la línea de tierra, que es la base de una pirámide de vértice V (-40, 70, 80):
– Hallar la sección por un plano.
– Verdadera magnitud de esa sección.
– Desarrollo del tronco de pirámide.
– Dibujar la geodésica que une M (punto medio de VA) con N (punto situado en VD y a 20 mm de V).

---

SOLUCIÓN

Desarrollo de la pirámide oblicua de base hexagonal.

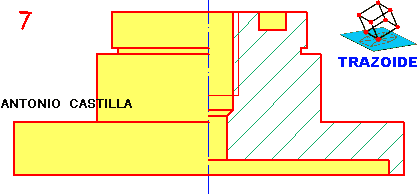
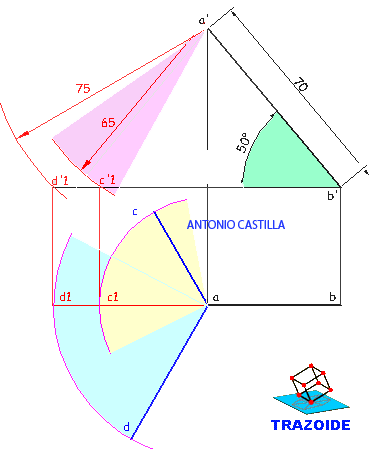
1 – En la proyección vertical hacer una paralela a la línea de tierra por la base y otra por el vértice. Trazar una tercera línea perpendicular a las dos (lo que está a la derecha). Esto nos servirá para hallar las verdaderas magnitudes.

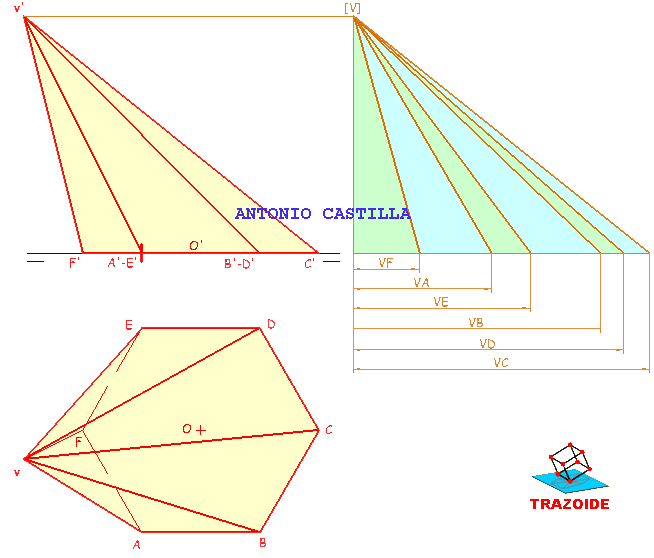
2 – Para hallar las verdaderas magnitudes de los triángulos que forman las caras laterales de la pirámide, se llevan las medidas de cada arista tomada en la proyección horizontal sobre la horizontal de las verdaderas magnitudes (están marcadas con una cota cada una).

3 – Se unen con el punto superior de la perpendicular [V], dando las verdaderas magnitudes de las aristas (las líneas oblicuas que parten de [V] ).

4 – Las verdaderas magnitudes de los lados de la base ya son conocidos, pues lo daban en el enunciado.

5 – Conocidas las tres verdaderas magnitudes de cada cara se van trazando los triángulos correspondientes.

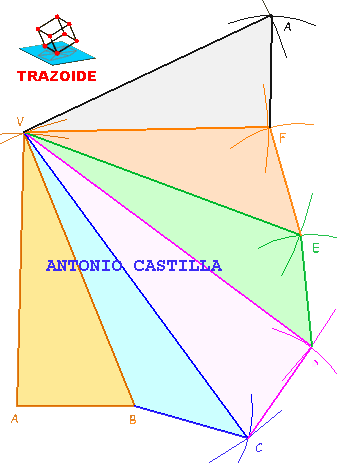
Trazado de la geodésica

6 – El punto N es rápidamente localizable tanto en proyección horizontal, vertical como en el desarrollo, por ser el punto medio de la arista V-A.

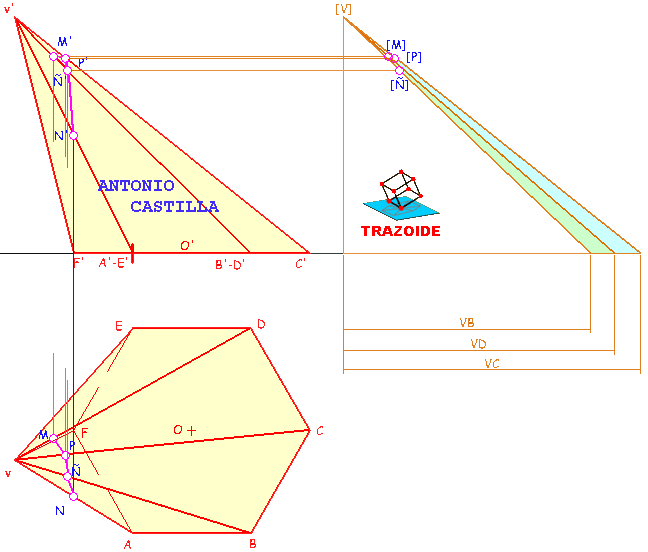
7 – El punto M está a 20 mm de V sobre la arista VD. Para ello, sobre el desarrollo (verdaderas magnitudes) se localiza el punto M a esos 20 mm. También se miden los 20 mm en la verdadera magnitud de VD sobre los triángulos de verdaderas magnitudes (punto [M] ).

8 – De ahí se lleva a la proyección vertical y horizontal.

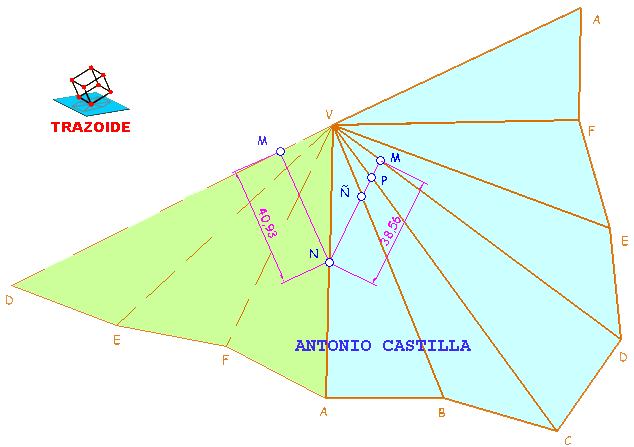
9 – Antes de localizar la geodésica sobre el desarrollo se deben plantear las dos posibles opciones, es decir, a partir de una de las aristas V-A se dibujan las caras VAF, VFE, VED (zona verde), situando los puntos M y N en este desarrollo ampliado.

10 – En el desarrollo se unen los puntos M y N (dos posibles trayectorias), comprobando cuál de las dos es el camino más corto entre ambos. Uno mide 38 mm y el otro 40 mm, luego, el valido es el primero.

11 – La geodésica atraviesa a las aristas laterales de la pirámide en los puntos Ñ y P.

12 – Se llevan las distancia V-Ñ y V-P desde el desarrollo al triángulo de las verdaderas magnitudes, [V]-[Ñ] y [V]-[P].

13 – Mediante paralelas a la línea de tierra se llevan a sus correspondientes aristas, obteniendo la proyección vertical. Mediante una perpendicular a la línea de tierra se bajan hasta la proyección horizontal.

14 – Ya solo queda unir los puntos en el mismo orden que estaban en el desarrollo, N-Ñ-P-M.

---

Inicio > Sistema diédrico > Desarrollos | | Vídeos sobre desarrollos

Inicio > Sistema axonométrico > Isométrica

Dibujar la perspectiva isométrica de la pieza dadas sus tres vistas :

---

SOLUCIÓN

La perspectiva isométrica está realizada viendo la pieza desde el lado inferior izquierdo de la planta :

---

Inicio > Sistema axonométrico > Isométrica ||

Inicio > Sistema axonométrico > Isométrica

Breve historia de la perspectiva isométrica.

---

SOLUCIÓN

La necesidad de dibujar elementos de máquinas, desde los inicios de la primera Revolución Industrial, se puso de manifiesto.

Como respuesta a los retos que se planteaban, William Farish, propuso en 1820, en la Universidad de Cambridge, su «perspectiva isométrica», acuñando por primera vez el nombre (On Isometrical Perspective).

La perspectiva isométrica formulada por Farish resolvía, con una gran sencillez, los complicados problemas métricos de las perspectivas con puntos de fuga. Dibujando siempre en la dirección de tres rectas que forman ángulos de 120°, se representan a la misma escala las tres magnitudes de los objetos: altura, anchura y profundidad.

La divulgación teórica de la perspectiva isométrica fue muy rápida, los tratadistas franceses de geometría descriptiva incluyeron inmediatamente la propuesta para explicarla como la proyección de un objeto del espacio sobre un plano; así, Theodore Olivier la recoge en su tratado de 1843, por vez primera, con el nombre de «proyección isométrica». En su afán científico de formular las leyes universales de la ciencia de la representación, bajo el concepto geométrico de proyección, establece una diferencia entre la «proyección isométrica ortogonal (sistema inglés)» y la «proyección isométrica oblicua (sistema francés)»; esta última es la denominada por él como «proyección militar o caballera».

---

Inicio > Sistema axonométrico > Isométrica || Vídeos sobre el sistema isométrico

isométrica – 965