Mes: octubre 2014

Ejercicios de equivalencias – 966

Inicio > Geometría plana > Equivalencias

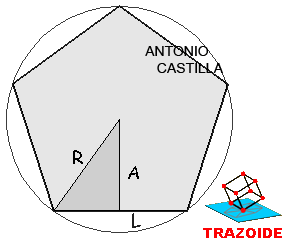
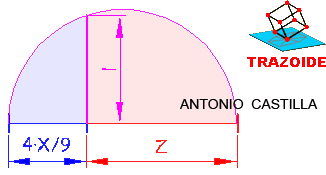
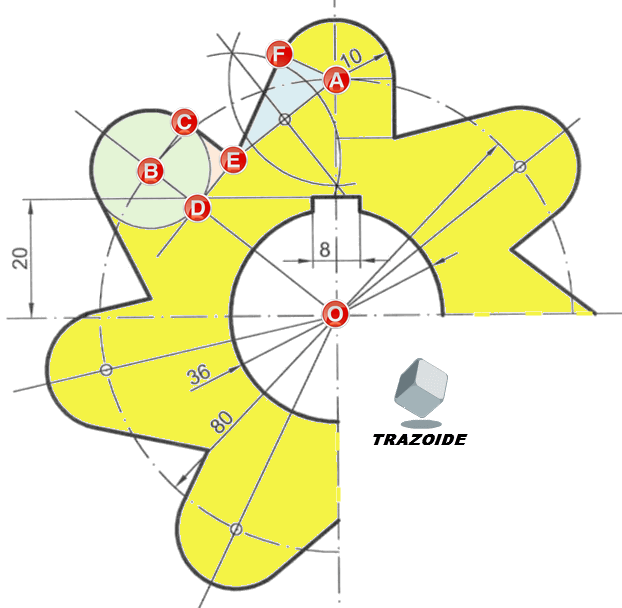
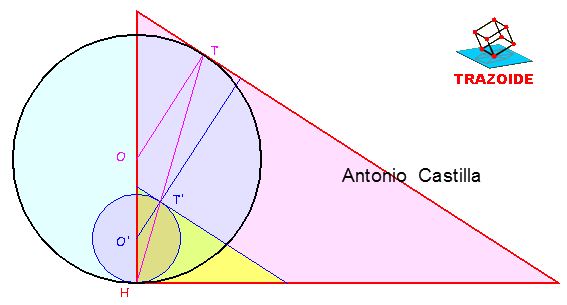
Rectángulo equivalente a un pentágono regular, estando la base y altura del rectángulo en un proporción de 3/1

---

SOLUCIÓN

Existen muchas formas de hacerlo :

OPCIÓN I

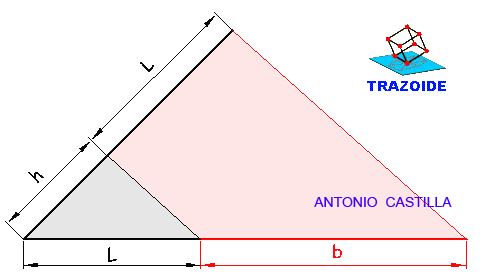
1 – El área del pentágono es 5·L·R/2, donde L es la medida del lado y R el radio de la circunferencia inscrita. El área del rectángulo es b·h, donde b es su base y h su altura. Y entre la base y la altura del rectángulo b/h = 3/1, o bien, b = 3·h.
2 – Igualando las áreas 5·L·R/2 = b·h, y sustituyendo, 5·L·R/2 = (3·h)·h.
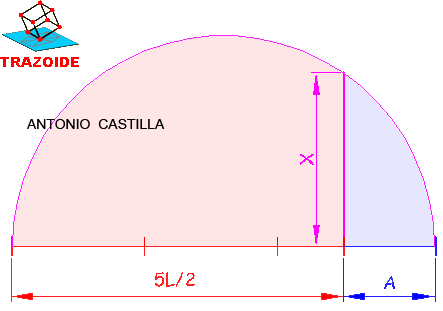
Reordenando, (5·L/6)·R = h·h.
3 – Plantear una media proporcional entre (5·L/6) y R, el resultado es h.
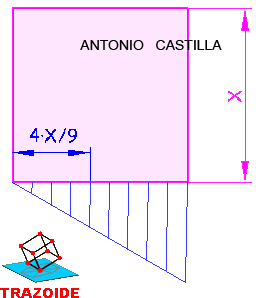
4 – Conseguido la altura, h, la base es b = 3·h

OPCIÓN II

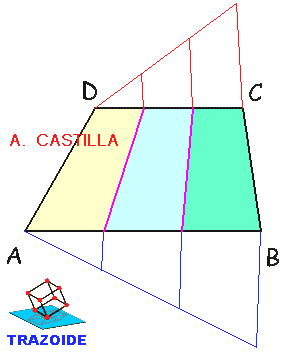
5 – Reducir el pentágono a un triángulo equivalente. Pulsar aquí para ver el procedimiento.
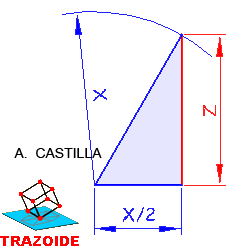
6 – El área del triángulo es B·H/2. Si la igualamos a la del rectángulo B·H/2 = b·h, sustituyendo como antes, B·H/2 = (3·h)·h. Y reordenadolo, B·H/6 = h·h.
7 – Resolver la media proporcional de B y H/6 para obtener h.

---

Inicio > Geometría plana > Equivalencias | | Vídeos sobre equivalencias

Ejercicios de equivalencias – 965

Inicio > Geometría plana > Equivalencias

Hallar un hexágono regular equivalente a un pentágono regular.

---

SOLUCIÓN

a – El área pentágono es 5·L·A/2, donde L es la longitud del lado y A su apotema.
b – Se iguala al área de un cuadrado de lado X, 5·L·A/2 = X·X. Mediante una media proporcional de (5·L/2) y A se determina el lado X del cuadrado.

c – Se halla 4/9 del lado del cuadrado.

d – Se traza un ángulo de 90º y sobre uno de sus lados se lleva la mitad del lado del cuadrado, X/2. Con centro en su extremo y radio el lado del cuadrado, X, se corta a la perpendicular. El cateto formado es Z.

e – Se halla la media proporcional entre 4X/9 y Z. El resultado es el lado, l, del hexágono buscado.

---

Inicio > Geometría plana > Equivalencias | | Vídeos sobre equivalencias

Ejercicios de equivalencias – 963

Inicio > Geometría plana > Equivalencias

División de un trapecio en varios equivalentes.

---

SOLUCIÓN

1 – Dividir ambas bases (los lados paralelos) en un número de partes iguales a los trapecios que se quieran obtener (en mi dibujo en tres).

2 – Unir las divisiones de ambas bases y las regiones entre ellas son los trapecios buscados.

---

Inicio > Geometría plana > Equivalencias | | Vídeos sobre equivalencias

Inicio > Geometría plana > Equivalencias

Dado un cuadrado de 60 mm de lado, construir el rectángulo equivalente de manera que uno de los lados mida 40 mm.

---

SOLUCIÓN

1 – Se plantea Área cuadrado = Área rectángulo, L·L = b·h, donde L es el lado del cuadrado, b es la base del rectángulo y h su altura. Supongamos que h = 40 mm. Reordenádolo L/h = b/L, tenemos una tercera proporcional, donde b es la incógnita.

2 – Se resuelve la tercera proporcional y se determina el valor de b.

3 – Dibujar el rectángulo conocida la base, b, y su altura, h.

 

---

 

Inicio > Geometría plana > Equivalencias | | Vídeos sobre equivalencias

 

equivalencias – 962

Inicio > Geometría plana > Enlaces y tangencias

Completar la figura representada, indicando la escala del dibujo. (Selectividad Valencia)

---

SOLUCIÓN

1 – Trazar una circunferencia de centro O y diámetro 80.

2 – Dividir la circunferencia en siete partes iguales. Cada división tomarla como centro de una circunferencia de radio 10, como los centros A y B.
3 – Unir las divisiones con el centro para obtener los ejes, OA, OB, …
4 – Por cada división trazar una perpendicular a su eje, como BC.
5 – Por donde la perpendicular corta a la circunferencia dibujar una paralela a su eje, como CE.
6 – Por donde la circunferencia corte a su eje, punto D se traza una nueva perpendicular, DE, cortando a la paralela anterior en E.
7 – Desde ese punto, E, trazar la tangente, EF, a la circunferencia del diente siguiente.
8 – Ahora se puede repetir lo mismo con el siguiente diente o mejor mediante giros de 360º/7 trazar los nuevos dientes.

 

---

Inicio > Geometría plana > Enlaces y tangencias | | Vídeos sobre enlaces y tangencias

enlaces – 118

Inicio > Geometría plana > Enlaces y tangencias

Realizar el siguiente grifo mediante enlaces y tangencias.

---

SOLUCIÓN

1 – Empezamos situando dos ejes perpendiculares que se cruzan en A.

2 – Sobre el eje horizontal, desde A, medir 65 hacia la izquierda (punto B).

3 – Desde B y hacia abajo medir 45 (punto C). Hacia derecha e izquierda dibujar una horizontal de 30/2 (punto K).

4 – Desde A en horizontal hacia la derecha medir 60 (punto D).

5 – Desde D dibujar un rectángulo de 36 x 5.

6 – Desde A y hacia arriba medir 45 (punto F). Hacia derecha e izquierda medir 36/2 (puntos I y M) y bajar verticales.

7 – Desde AD dibujar hacia arriba una paralela a 24/2.

8 – Desde G y hacia la izquierda medir 6 y ese es el primer centro, dibujar el arco de radio 6.

9 – Desde I medir 20 hacia la izquierda y dibujar una lÍnea vertical. Desde AD dibujar hacia arriba una paralela a (24/2) + 20. Donde se corte la horizontal y la vertical es el centro J de la circunferencia de radio 20.

10 – Desde K medir 5 en vertical y desde ahÍ 25 hacia la derecha, este es el centro L de la circunferencia de radio 25.

11 – Con centro en L y radio 35 dibujar una circunferencia.

12 – Con centro en L y radio 35 + 20 dibujar un arco. Desde M hacia la izquierda medir 20 y dibujar una vertical. Donde la vertical y el arco se corten es el centro N del arco de radio 20.

13 – Desde F y hacia abajo medir 40 y este es el centro O. Unir O con L y donde corte al arco de centro L y radio 25 es el punto de tangencia P. Con centro en O y radio hasta P dibujar el arco.

14 – Desde Q y hacia la izquierda medir 6 y ese es el centro R del arco de radio 6.

15 – Desde AD y hacia abajo medir 24/2 y dibujar una horizontal.

16 – Con centro en O y radio la suma de OP más 30 dibujar un arco. Dibujar un eje horizontal paralelo a AD hacia abajo a una distancia de (24/2) + 30. Donde esta última corte al arco es el centro S de la circunferencia de radio 30.

 

---

Inicio > Geometría plana > Enlaces y tangencias | | Vídeos sobre enlaces y tangencias

 

enlaces – 117

Ejercicios resueltos de enlaces y tangencias – 116

Inicio > Geometría plana > Enlaces y tangencias

Dado un triángulo rectángulo, construir una circunferencia tangente a la hipotenusa, que pase por el vértice del ángulo recto y que tenga su centro en uno de los catetos.

---

SOLUCIÓN

Mediante una homotecia.

1 – Dibujar una circunferencia cualquiera con centro cualquiera sobre un cateto, O’ y radio hasta el ángulo recto, H.

2 – Desde su centro, O’, dibujar una perpendicular a la hipotenusa, que nos da el punto de tangencia, T’, en un triángulo homotético al dado (el triángulo relleno de amarillo, aunque no hace falta dibujarlo).
3 – Unir el ángulo recto H (el centro de homotecia) con el punto de tangencia T’ y donde corte a la hipotenusa es el punto de tangencia de la circunferencia buscada, T.
4 – Por el punto de tangencia, T, trazar una perpendicular a la hipotenusa y obtenemos el centro de la circunferencia buscada, O.

---

Inicio > Geometría plana > Enlaces y tangencias | | Vídeos sobre enlaces y tangencias

Inicio > Geometría plana > Enlaces y tangencias

Realizar el siguiente soporte para eje :

---

SOLUCIÓN

1 – Sitúa el centro A y un eje vertical AG.

2 – Con centro en A y diámetros 66, 42 y 22 dibujar las tres circunferencias superiores.

3 – A partir de AG dibujar otro eje separado 30º y sobre él a partir de A medir 98 para obtener B.

4 – Con centro en B y diámetros 40 y 20 dibujar ambas circunferencias.

5 – Dibujar dos paralelas al eje AB hacia cada lado separados 6/2.

6 – Dibujar unas paralelas a las anteriores separadas 3 mm y con centro en A y radio (66/2) + 3 trazar un arco. Donde corte a la paralela son los centros de los arcos D. Con centro en B y radio (40/2) + 3 hacer otro arco que al cortar a las paralelas da los centros de los arcos E.

7 – Con centro en A y radio 100 – (66/2) dibujar un arco. Con centro en B y radio 100 – (40/2) trazar otro arco. Donde ambos se corten es el centro F del arco de radio 100.

8 – Con centro en B y radio (40/2) + 33 dibujar un arco. Donde el arco corte al eje vertical que parte de A es el centro G del arco de radio 33.

9 – Con centro en A y radio 42/2 dibujar una circunferencia.

10 – Con centro donde la circunferencia anterior corte al eje vertical y con radio 42/2 hacer un arco que corte a dicha circunferencia. Volver a tomar centro donde el arco corta a la circunferencia y con el mismo radio hacer otro arco. Seguir repitiendo con lo que conseguimos dividir la circunferencia en seis partes iguales que serán los centros de las seis circunferencias de radio 8/2.

 

---

Inicio > Geometría plana > Enlaces y tangencias | | Vídeos sobre enlaces y tangencias

 

enlaces y tangencias – 115

Ejercicios resueltos de enlaces y tangencias – 114

Inicio > Geometría plana > Enlaces y tangencias

A partir de la siguiente figura dibujar, indicando claramente los centros y puntos de tangencia de los diferentes arcos de enlaces :

---

SOLUCIÓN

1 – Coloca el centro A y su semicircunferencia de radio 200/2.

2 – Desde A y hacia la derecha medir 400 y hacia arriba otros 400, con lo que se obtiene el centro B. Dibujar su circunferencia de radio 150.
3 – Desde los extremos de la semicircunferencia A trazar sendas horizontales.
4 – Dibujar una paralela a la horizontal superior a una distancia de 150. Con centro en B y radio 150 + 150 trazar un arco. Donde el arco corte a la paralela es el centro C.
5 – A 200 del centro B y hacia la derecha dibujar una línea vertical y otra hacia la izquierda a 250 – 200. Con centro en B y radio 250 – 150. Donde corte a la vertical de la izquierda es el centro E.
6 – Dibujar una línea vertical paralela a la de la derecha a 150 hacia la izquierda. Dibujar una línea horizontal paralela a la horizontal inferior a 150. Donde se corten las dos es el centro D.

---

Inicio > Geometría plana > Enlaces y tangencias | | Vídeos sobre enlaces y tangencias

Inicio > Geometría plana > Enlaces y tangencias

A partir de la siguiente figura dibujar, indicando claramente los centros y puntos de tangencia de los diferentes arcos de enlaces de una llave fija, siendo su extremo un óvalo.

---

SOLUCIÓN

1 – Dibujar el eje vertical AB de longitud 145 mm.

2 – Desde el punto A hacer un nuevo eje que forme 60º respecto del primero.

3 – Con centro en A dibujar un óvalo de eje mayor 56 y eje menor 40. Lo puedes ver pulsando aquí. El óvalo tendrá cuatro centros C1, C2, C3 y C4.

4 – Hacer dos paralelas al eje menor del óvalo a 28/2 hacia cada lado.

5 – Donde las dos paralelas toquen al eje mayor del óvalo trazar dos líneas que formen 30º con el susodicho eje.

6 – Con centro en B y radio 8 mm dibujar una circunferencia.

7 – Sobre el eje vertical AB y desde B medir 114 mm, punto D.

8 – A partir de D y en horizontal llevar 25/2 hacia cada lado.

9 – Hacer las tangentes desde los extremos anteriores hasta la circunferencia de centro B.

10 – Dibujar una paralela a la tangente de la derecha a 12 mm y con centro en C1 y radio la suma del radio de C1 más 12 mm hacer un arco. Donde el arco se corte con la paralela es el centro E.

11 – Dibujar una paralela a la tangente de la izquierda a 19 mm y con centro en C4 y radio la suma del radio de C4 más 19 mm hacer un arco. Donde el arco se corte con la paralela es el centro F.

---

Inicio > Geometría plana > Enlaces y tangencias | | Vídeos sobre enlaces y tangencias