Categoría: Uncategorized

Inicio > Geometría plana > Afinidad

Forma de relacionar una elipse y una circunferencia mediante afinidad, respecto de sus ejes principales.

---

SOLUCIÓN

La elipse se puede transformar en una circunferencia mediante una afinidad. Realizar las operaciones que sean necesarias en la circunferencia, que suele ser más fácil, y después llevar lo averiguado a la elipse mediante la afinidad.
Esto tiene «millones» de aplicaciones: intersección de una recta con una elipse, tangente a una elipse desde un punto exterior, etc.

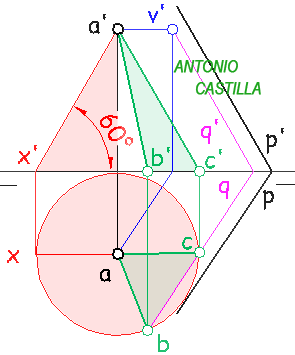
Para definir la afinidad son necesarios determinar varios elementos: el eje de afinidad, la dirección de afinidad, un par de puntos afines y la circunferencia afín a la elipse.

Circunferencia afín: Tendrá de centro el mismo de la elipse y de radio el semieje mayor o el semieje menor. Se puede utilizar indistintamente una o la otra (a veces incluso las dos), pero casi siempre se utiliza el mayor por dar más claridad.

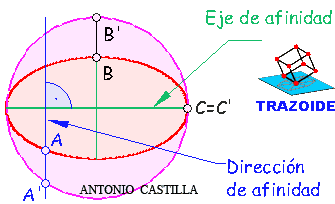
Eje de afinidad: Es el eje mayor si se ha utilizado este como diámetro de la circunferencia o el eje menor cuando se utiliza él como diámetro de la circunferencia.

Dirección de afinidad: Es ortogonal (perpendicular al eje de afinidad).

Par de puntos afines: Desde el centro de la elipse se levanta una perpendicular al eje de afinidad y donde corte a la elipse y a la circunferencia son dos puntos afines. El punto de corte con la elipse es siempre uno de los extremos del eje mayor o menor. En realidad, la recta corta en cuatro puntos (dos de la elipse y otros dos de la circunferencia), se pueden tomar los dos que quedan al mismo lado del eje (afinidad de razón positiva) o uno a cada lado (afinidad negativa), es indiferente y a veces conviene uno más que el otro para que no dé puntos de corte con el eje muy alejados.

Si se tiene un punto cualquiera de la elipse se traza una perpendicular al eje y donde corte a la circunferencia es su afín.

Conocidos todos estos elementos se puede plantear una afinidad, en la que también se transformarán los demás elementos (puntos, rectas, etc.) con las mismas relaciones de afinidad.

---

Inicio > Geometría plana > Afinidad | | Vídeos sobre afinidad

afinidad – 979

Inicio > Sistema diédrico > Ángulos en diédrico

Dados el punto A(-5, 7, 12) y el plano P(8, 12, 14), dibujar las rectas que pasan por A, forman 60º con el plano horizontal de proyección y son paralelas al plano P.

---

 

SOLUCIÓN

1 – Por la proyección vertical del punto A se traza una línea que forme con la línea de tierra el ángulo dado con el plano horizontal de proyección, 60º.

2 – Donde toque a la línea de tierra, x’, se baja hasta una paralela a la línea de tierra que pase por la proyección horizontal de A. Esto nos da la proyección horizontal, x.

3 – Con centro en la proyección horizontal de A y radio hasta x hacer una circunferencia.

4 – Por el punto A dibujar un plano paralelo al dado:

4.a -Trazar por el punto A una recta horizontal (en azul), con su proyección horizontal paralela a la traza horizontal del plano.

4.b – Hallar la traza vertical de esa recta, v’.

4.c – Por la traza vertical hacer una paralela a la traza vertical del plano dado, p’, lo que nos da la traza vertical, q’ del plano buscado.

4.d – Por donde corte a la línea de tierra una paralela a la traza horizontal del plano, p, y se tiene la traza horizontal del plano, q.

5 – Los puntos donde la traza horizontal q corte a la circunferencia, b y c, al unirlos con a dan las proyecciones horizontales de las dos posibles soluciones, a-b y a-c.

6 – Subirlos hasta la línea de tierra, b’ y c’, y unirlos con a’ para determinar las proyecciones verticales de las dos posibles soluciones.

---

 

Inicio > Sistema diédrico > Ángulos en diédrico | | Vídeos sobre ángulos

 

Inicio > Sistema diédrico > Ángulos en diédrico

Determinar el ángulo formado por dos planos (sin utilizar cambios de plano).

---

SOLUCIÓN

MÉTODO PRIMERO

1 – Elegir un punto cualquiera, A.

2 – Trazar desde A dos rectas perpendiculares a los planos.

3 – Las dos rectas perpendiculares forman un plano, abatir sendas rectas respecto del plano que forman.

4 – En el abatimiento se mide la verdadera magnitud del ángulo formado por las dos rectas, N .

5 – El ángulo entre los dos planos, M, es el suplementario del ángulo entre las dos rectas, M = 180º – N.

MÉTODO SEGUNDO

a – Hallar la intersección entre los dos planos, I.

b – Dibujar un plano perpendicular a la intersección de los dos planos, I, en cualquier lugar.

c – Hallar las intersecciones, X e Y, del plano perpendicular con los dos planos dados, P y Q .

d – Abatir las dos rectas intersección, X e Y, respecto del plano perpendicular.

e – El ángulo, M, formado por las dos rectas X e Y abatidas es el ángulo formado por los dos planos.

---

Inicio > Sistema diédrico > Ángulos en diédrico | | Vídeos sobre ángulos

Ejercicios de ÁNGULOS en diédrico – 986

Inicio > Sistema diédrico > Ángulos en diédrico

 

Determinación de las trazas de un plano conocidos los dos ángulos que forma con los planos de proyección.

---

SOLUCIÓN

1 – Por un punto cualquiera de la línea de tierra, O, se traza una circunferencia de radio cualquiera.

2 – Por encima de la línea de tierra se dibuja una tangente a la circunferencia anterior con el ángulo que forma el plano buscado con el plano horizontal de proyección, H.

3 – Por debajo de la línea de tierra se dibuja una tangente a la circunferencia con el ángulo que forma el plano buscado con el plano vertical de proyección, V.

4 – Por O se levanta una perpendicular a la línea de tierra que corta a las tangentes anteriores en X e Y.

5 – Con centro en O y radio hasta donde las tangentes cortan a la línea de tierra, puntos 1 y 2, se trazan dos semicircunferencias en el lado contrario a donde está cada tangente.

6 – Desde X e Y se dibujan tangentes a las dos semicircunferencias. Esas son las trazas del plano buscado, P.

7 – Se hace un plano paralelo al obtenido por donde indique el problema.

 

---

Inicio > Sistema diédrico > Ángulos en diédrico | | Vídeos sobre ángulos

 

Inicio > Geometría plana > Triángulos

Triángulo del que se conoce un vértice, A, el baricentro, G, y el pie, X, de la bisectriz del ángulo A.

---

SOLUCIÓN

1 – Unir el vértice, A, con el baricentro, G.

2 – Dividir AG en dos partes iguales.

3 – A partir de G prolongar AG y llevar una de las partes obtenidas. Esto da m punto medio del lado BC.

4 – Unir m con X, en esta recta esta el lado BC.

5 – Por el punto m hacer una perpendicular a mX.

6 – Unir A con X hasta cortar a la perpendicular anterior (punto Y).

7 – Hallar la mediatriz de AY y donde corte a la perpendicular por m es el circuncentro O.

8 – Con centro en O y radio hasta A hacer una circunferencia.

9 – Prolongando Xm se obtienen los vértices B y C sobre la circunferencia.

---

Inicio > Geometría plana > Triángulos | | Vídeos sobre triángulos

Inicio > Geometría plana > Triángulos

Construir un triángulo un conocidos un vértice A, el baricentro G y el circuncentro O.

---

SOLUCIÓN

Para resolverlo debes conocer la recta de Euler (otros le llaman segmento de Euler).

El circuncentro, el baricentro y el ortocentro está en una misma recta, la recta de Euler.

La distancia que hay desde el baricentro hasta el ortocentro es el doble de la que hay entre el baricentro y el circuncentro.

Conocido el fundamento los pasos a seguir son estos:

1 – Con centro en el circuncentro, C, y radio hasta el vértice dado, A, se traza una circunferencia, la circunscrita. En ella están los dos vértices que faltan.

2 – Une el circuncentro con el baricentro, G (recta de Euler).

3 – Lleva el doble de la distancia que hay entre el circuncentro y el baricentro sobre la recta anterior, a partir del baricentro y hacia el lado que no está el circuncentro; con lo que obtienes el ortocentro, O.

4 – Une el vértice dado, A, con el ortocentro y tienes la altura (la recta sobre la que está, no su longitud). El lado opuesto al vértice A será perpendicular a esa altura.

5 – Por el circuncentro haz una paralela a esa altura. Esta nueva recta será la mediatriz del lado opuesto al vértice A, ya que los circuncentros se consiguen con las mediatrices que son perpendiculares a los lados y por tanto paralelos a las alturas que también son perpendiculares a los lados.

6 – Unir el vértice dado, A, con el baricentro. Esta recta será la mediana.

7 – La mediana llega hasta el punto medio del lado opuesto del vértice y la mediatriz también pasa por ese punto medio, M, por lo que donde la mediatriz corte a la mediana tienes el punto medio del lado.

8 – Por el punto medio del lado, M, se hace una perpendicular a la altura y donde corte a la circunferencia circunscrita se obtienen los otros dos vértices del triángulo.

---

Inicio > Geometría plana > Triángulos | | Vídeos sobre triángulos

Inicio > Geometría plana > Triángulos

Construir un triángulo rectángulo conocido el lado c = 80 mm, la situación exacta del baricentro y la circunferencia circunscrita.

---

SOLUCIÓN

1 – Prolonga la recta formada por el baricentro y el centro de la circunferencia circunscrita hasta cortar a la circunferencia.

2 – Ese punto es el vértice del ángulo recto.

3 – Con centro en ese vértice y radio el lado «c» se traza un arco.

4 – Donde corta a la circunferencia circunscrita es el segundo vértice.

5 – El tercer vértice se puede lograr uniendo ese segundo vértice con el centro de la circunferencia circunscrita hasta cortarla; o bien con respecto al cateto «c» se levanta el otro cateto perpendicular.

---

Inicio > Geometría plana > Triángulos | | Vídeos sobre triángulos

Inicio > Geometría plana > Triángulos

Hallar un triángulo, ABC, del que se conoce la distancia OA y OB, siendo O el baricentro y que el lado AB es la media proporcional de AO y OB.

---

SOLUCIÓN

1 – Hallar la media proporcional entre OA y OB, y este es el lado AB.

2 – Colocar el lado AB.

3 – Con centro en A y radio OA se dibuja un arco. Con centro en B y radio OB se dibuja otro arco. Donde se corten los dos arcos es el baricentro O.

4 – Unir el punto medio, M, del lado AB con el baricentro O.

5 – Prolongar OM más allá del baricentro O y llevar sobre ella el doble de la distancia OM. Esto nos da el vértice C.

---

Inicio > Geometría plana > Triángulos | | Vídeos sobre triángulos

Triángulo conocido un lado, el ángulo opuesto y la altura

Inicio > Geometría plana > Triángulos

Hallar un triángulo conocido un lado, AB = 60 mm, el ángulo opuesto C = 60º y la altura respecto del lado contiguo, hb = 50 mm.

---

SOLUCIÓN

MÉTODO 1º

1 – Colocas el lado AB.

2 – Con centro en B y radio hb se hace un arco.
3 – Desde A se traza la tangente al arco.
4 – Desde cualquier punto de esa tangente se traza un ángulo de 60º.
5 – Dibujar una paralela a ese ángulo por el vértice B y donde corte a la tangente es el tercer vértice C.

MÉTODO 2º

6 – Se construye un ángulo de 60º, su vértice es C.

7 – Se dibuja una perpendicular a uno de los lados (magenta) del ángulo y se mide sobre ella la altura hb.
8 – Dibujar una paralela a ese lado por esa distancia y donde corte al otro lado (verde) del ángulo es el segundo vértice B.
9 – Con centro en B y radio AB se hace un arco.
10 – Donde el arco corte al primer lado del ángulo da el vértice A.

MÉTODO 3º

11 – Colocas el lado AB.

12 – Trazas el arco capaz de 60º respecto de AB.
13 – Con centro en B y radio hb se dibuja un arco.
14 – Desde A se traza la tangente al arco.
15 – Donde la tangente corte al arco capaz es el tercer vértice C.

---

Inicio > Geometría plana > Triángulos | | Vídeos sobre triángulos

Inicio > Geometría plana > Trapecios

Obtener un trapecio escaleno dados sus lados paralelos 50 y 30 mm y sus diagonales 40 y 65 mm.

---

SOLUCIÓN

1 – Se coloca el lado mayor de los lados paralelos (50 mm), a cuyos extremos los llamaré A y B.

2 – A continuación del segmento anterior se coloca la otra base (30 mm), a cuyo punto final llamaré X.

3 – Con centro en A y radio el de primera diagonal (40 mm) se hace un arco.

4 – Con centro en X y radio el de la segunda diagonal (65 mm) se hace un segundo arco.

5 – Donde se corten los dos arcos es el tercer vértice buscado, el C.

6 – Por C se hace una paralela a AB.

7 – Con centro en el extremo B y radio el de la segunda diagonal (65 mm) se hace un arco que corte a la paralela anterior, siendo el punto de corte el cuarto vértice D.

---

Inicio > Geometría plana > Trapecios | | Vídeos sobre trapecios