Mes: octubre 2014

Inicio > Geometría plana > Enlaces y tangencias

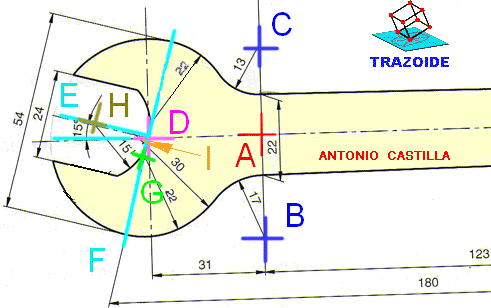
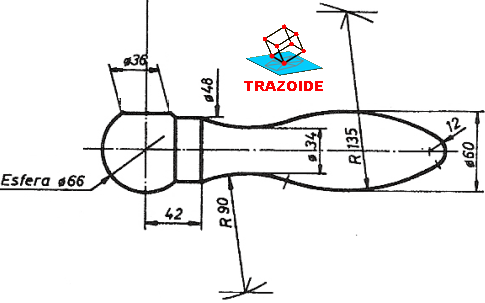
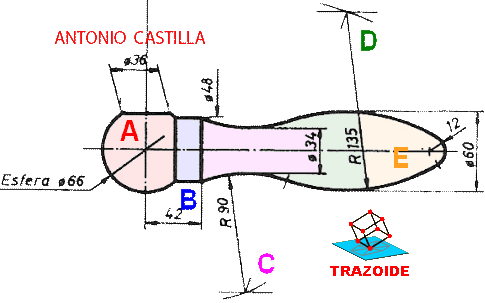
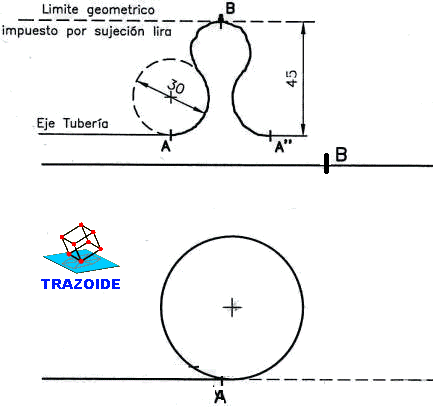
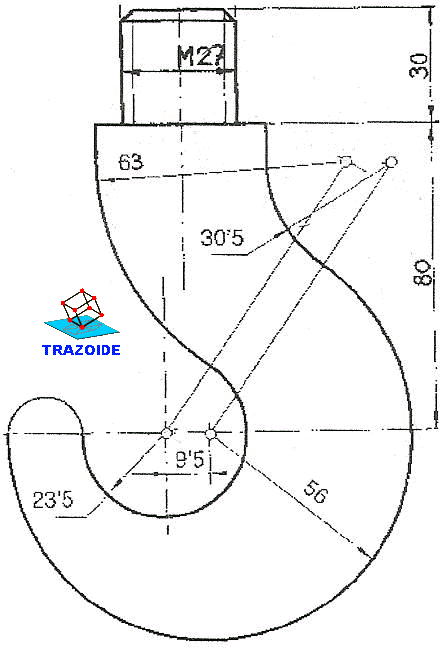
Dibujar el gancho de la figura con las cotas indicadas, dejando constancia de los centros y puntos de tangencia :

---

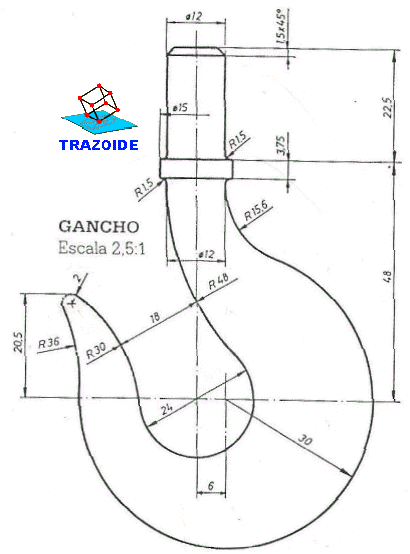
SOLUCIÓN

1 – Colocar el primer centro A y con diámetro 24 dibujar una circunferencia.

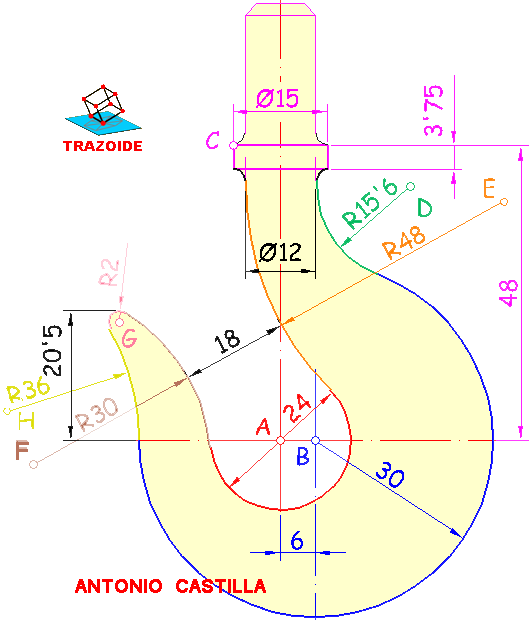
2 – Medir 6 mm hacia la derecha del punto A para situar el centro B. Con centro en B y radio 30 dibujar una circunferencia.

3 – A partir del punto A medir 48 mm en vertical y 15/2 hacia la izquierda para situar el vértice C. A partir de C dibujar un rectángulo de largo 15 y alto 3’75 hacia abajo.

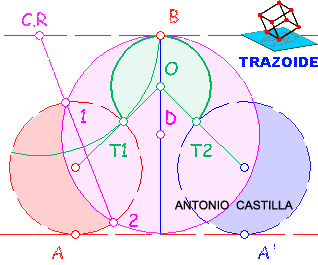
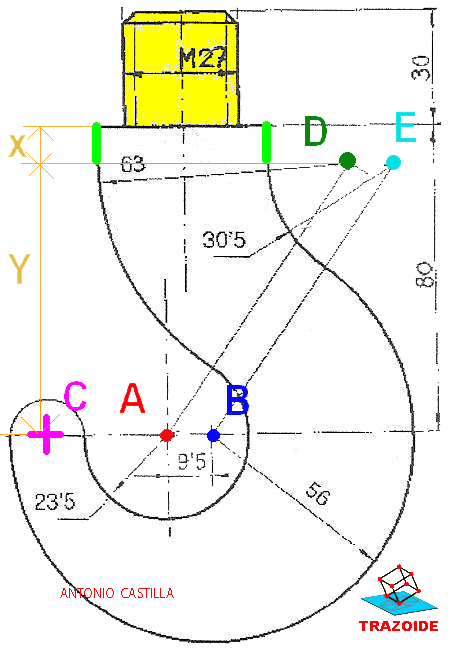
4 – Hacer una paralela al eje vertical que pasa por A separado (24/2)+15’6 hacia la derecha. Con centro en B y radio 30+15’6 se dibuja un arco. Donde el arco corte a la paralela es el centro D de la circunferencia de radio 15’6.

5 – Hacer una paralela al eje vertical que pasa por A separado 48-(24/2) hacia la derecha. Con centro en A y radio (24/2)+48 se traza un arco. Donde el arco corte a la paralela es el centro E de la circunferencia de radio 48.

6 – Con centro en E y radio 48+18+30 trazar un arco. Con centro en A y radio (24/2)+30 dibujar otro arco. Donde se corten ambos es el centro F del arco de radio 30.

7 – Con centro en F y radio 30-2 dibujar un arco. Hacer una paralela al eje horizontal que pasa por A 20’5-2 mm hacia arriba. Donde el arco corte a la paralela es el centro G del arco de radio 2.

8 – Con centro en G y radio 2+36 trazar un arco. Con centro en B y radio 30+36 trazar otro arco. Donde se corten los dos arcos es el centro H del arco de radio 36

 

---

Inicio > Geometría plana > Enlaces y tangencias | | Vídeos sobre enlaces y tangencias

 

enlaces y tangencias – 12

Ejercicios resueltos de enlaces y tangencias – 11

Inicio > Geometría plana > Enlaces y tangencias

Circunferencia tangente a dos circunferencias de igual radio, 60 mm, y a otra situada en la mediatriz de los centros de las anteriores de radio 80 mm.

---

SOLUCIÓN

1 – Restar el radio de la menor al de la mayor, 80 – 60 = 20 mm, y con centro en el de la mayor dibujar una nueva circunferencia.
2 – El problema ha quedado reducido a dos puntos, los centros de las dos circunferencias menores, y a una circunferencia (la obtenida al restar los radios).
3 – Por el centro, O, de la circunferencia dada se hace una perpendicular a la recta que pasa por los puntos P y Q.

4 – El punto de corte de esta última recta con la circunferencia se une con uno de los dos puntos dados.
5 – A esta recta se le halla la mediatriz y donde corte a la perpendicular de PQ es el centro, C, de la circunferencia buscada.
Existe una segunda solución (no dibujada) hallando la mediatriz entre uno de los puntos y donde la perpendicular a PQ corta a la circunferencia (a la derecha).

---

Inicio > Geometría plana > Enlaces y tangencias | | Vídeos sobre enlaces y tangencias

Inicio > Geometría plana > Enlaces y tangencias

Dibujar la siguiente llave fija con sus enlaces, tangencias y puntos de tangencia :

---

SOLUCIÓN

1 – Colocar un eje horizontal de longitud 123 mm, siendo uno de sus extremos A.

2 – Por sus extremos levantar sendas perpendiculares que midan 22 y 20 mm la de la izquierda y derecha respectivamente. Unir sus extremos y ya tenemos el mango de la llave fija.

3 – Centrémonos en la boca izquierda. Por los extremos del mango levantar perpendiculares a los lados del mango. En la de arriba medir 13 y en la de abajo 17 mm. Esto nos da los centros B y C. Trazar sus arcos.

4 – Prolongar el eje hacia la izquierda 31 mm, obteniendo el centro D.

5 – Levantar el eje DE con 15º respecto del eje horizontal. El eje DF es perpendicular al eje DE.

6 – Con centro en D y radio 54/2 trazar un arco.

7 – A partir de D y sobre el eje DE medir 15 mm para obtener el centro H. Dibujar su arco.

8 – Trazar dos paralelas al eje DE separadas 24/2 de ese eje. Junto con el arco anterior esto forma la boca de la llave.

9 – Con centro en C y radio 13 + 22 dibujar un arco. Con centro en D y radio (54/2) – 22 se dibuja un segundo arco. Donde se corten los dos es el centro del arco de radio 22 mm de la parte superior.
10 – Sobre el eje DF y a partir de donde el arco de radio 54/2 corte a ese eje se mide una distancia de 22 mm para obtener el centro G. Con centro en G y radio 22mm trazar un arco.

11 – Con centro en B y radio 17 + 30 dibujar un arco. Con centro en G y radio 30 – 22 se dibuja un segundo arco. Donde se corten los dos es el centro I del arco de radio 30 mm de la parte inferior.

 

---

Inicio > Geometría plana > Enlaces y tangencias | | Vídeos sobre enlaces y tangencias

 

Ejercicios resueltos de enlaces y tangencias – 9

Inicio > Geometría plana > Enlaces y tangencias

Circunferencias tangentes a dos rectas, R y S, y que pasen por un punto, P, que está en la bisectriz de las dos rectas

---

SOLUCIÓN

1 – Por el punto dado, P, dibujar una perpendicular a la bisectriz.

2 – Donde corte, X, a una de las rectas dadas, R o S, se toma como centro de un arco de radio hasta el punto dado, P.
3 – Desde donde el arco corte a la recta, T1 y T2, levantar perpendiculares a la recta hasta cortar a la bisectriz, O1 y O2.
4 – Estos últimos puntos, O1 y O2, son los centros de las circunferencias buscadas de radio hasta los puntos de tangencia, T1 y T2.

---

Inicio > Geometría plana > Enlaces y tangencias | | Vídeos sobre enlaces y tangencias

Ejercicios resueltos de enlaces y tangencias – 8

Inicio > Geometría plana > Enlaces y tangencias

Hallar las circunferencias tangentes a tres circunferencias de distinto radio

---

SOLUCIÓN

1 – Restar el radio de la circunferencia menor a las otras dos y dibujar, en sus mismos centros, circunferencias de radio esa diferencia.
2 – El problema ha quedado reducido a trazar las circunferencia tangentes a dos circunferencias (las que se obtienen al restar los radios) y a un punto (el centro de la circunferencia de radio menor). Utiliza cualquiera de los procedimientos que te indico más abajo para resolverlo.
3 – Existe una solución más que consiste en sumar el radio de la circunferencia menor a las otras dos y dibujar, en sus mismos centros, circunferencias de radio esa suma.
4 – El problema vuelve ha quedar reducido a trazar las circunferencia tangentes a dos circunferencias (las que se obtienen al sumar los radios) y a un punto (el centro de la circunferencia de radio menor). Consulta en el índice las formas de resolverlo, caso CCP.

---

Inicio > Geometría plana > Enlaces y tangencias | | Vídeos sobre enlaces y tangencias

Ejercicios resueltos de enlaces y tangencias – 6

Inicio > Geometría plana > Enlaces y tangencias

Realizar el puño de manivela con las medidas de la figura :

---

SOLUCIÓN

A – Dibujar una circunferencia de centro A y diámetro 66

B – A partir del centro A y sobre el eje vertical medir 48/2 hacia cad lado. Trazar dos paralelas al eje horizontal hasta tocar a la circunferencia y uniendo los dos puntos se obtiene el rebaje de la derecha.
C – A partir del centro A y hacia la derecha dibujar una paralela al eje vertical separada 42. Completar e rectángulo, azul, en contacto con la esfera
D – Con centro en el vértice B del rectángulo y radio 90 trazar un arco. Dibujar una paralela al eje horizontal hacia abajo a una distancia de (34/2)+90. Donde corte al arco anterior es el centro C. Trazar el arco de radio 90
E – Con centro en C y radio 90+135 trazar un arco. Dibujar una paralela al eje horizontal hacia arriba a una distancia de 135-(60/2). Donde corte al arco anterior es el centro D. Trazar el arco de radio 135
F – Con centro en D y radio 135-12 se dibuja un arco. Donde corte al eje horizontal es el centro E. Trazar el arco de radio 12

---

Inicio > Geometría plana > Enlaces y tangencias | | Vídeos sobre enlaces y tangencias

Ejercicios resueltos de enlaces y tangencias – 5

Inicio > Geometría plana > Enlaces y tangencias

Circunferencia inscrita a un sector circular, AOB, de radio 70 mm y ángulo 60º.

---

SOLUCIÓN

1 – Hallar la bisectriz, OX, del ángulo, AOB, que forma el sector circular

2 – Trazar la tangente, XY, al arco desde el punto, X, donde la bisectriz la toca
3 – Prolongar uno de los lados del sector circular, OA, hasta cortar a la tangente, Y
4 – Hallar la bisectriz del ángulo, OYX, que forma la tangente con la prolongación del lado
5 – Donde esta última bisectriz corte a la primera bisectriz es el centro, C, de la circunferencia buscada

---

Inicio > Geometría plana > Enlaces y tangencias | | Vídeos sobre enlaces y tangencias

Ejercicios resueltos de enlaces y tangencias – 4

Inicio > Geometría plana > Enlaces y tangencias

 

Se tiene que construir una LIRA DE DILATACIÓN (de la forma indicada en el croquis) a insertar en una tubería lineal, dada por su eje y con dimensiones a escala para que encaje en el papel. Se trata de Encontrar la forma geométrica de la lira, para que se pueda construir, el punto A’ y la forma de la circunferencia que pase por B. Partir de los datos que se indican en el dibujo.

DATOS:
— El punto B donde se sujetará la LIRA, está en un plano a 45 mm del eje de la tubería y su posición se indica en el dibujo.
— El radio de curvatura de la tubería en el inicio en A es de 30 mm.
— La figura de la LIRA es simétrica

---

SOLUCIÓN

Puedes ver cómo resolver tangencias mediante potencia explicado en un vídeo pulsando aquí.

a – Dibujar una perpendicular a la recta superior por el punto B

b – Con centro en cualquier punto, D, de esa perpendicular trazar una circunferencia que pase por B
c – Unir los puntos, 1 y 2, de corte de la anterior con la circunferencia dada, hasta cortar a la recta superior en C.R
d – Con centro en C.R y radio hasta B dibujar un nuevo arco. Donde corte a la circunferencia dada es el punto de tangencia T1
e – Unir el centro de la circunferencia dada con T1 y donde corte a la perpendicular que pasaba por B es el centro de la circunferencia buscada, O

 

---

Inicio > Geometría plana > Enlaces y tangencias | | Vídeos sobre enlaces y tangencias

 

Inicio > Geometría plana > Enlaces y tangencias

Realizar el siguiente gancho, marcando sus centros y puntos de tangencia :

---

SOLUCIÓN

1 – Hacer dos ejes que se crucen perpendiculares. El punto de encuentro es el centro A

2 – Con centro en A y radio 23’5 trazar un arco
3 – A partir de A y hacia la derecha, dibujar el centro B separado 9’5 mm del centro A. Con centro en B y radio 56 trazar otro arco
4 – Prolongar el arco de A y B hasta cortar al eje horizontal que pasa por A y B. El centro C está en el punto medio de donde esos dos arcos corten al eje horizontal.
5 – Si nos han dado la medida Y, hacer una paralela al eje horizontal a una distancia Y desde A. Si nos han dado la medida X, hacer una paralela al eje horizontal a una distancia 80 – X.
6 – Con centro en A y radio 23’5 + 63 hacer un arco. Donde este arco corte a la horizontal obtenida con la distancia X o Y es el centro D
7 – Con centro en B y radio 56 + 30’5 hacer otro arco. Donde corte a la misma horizontal anterior es el centro E

 

---

Inicio > Geometría plana > Enlaces y tangencias | | Vídeos sobre enlaces y tangencias

 

     

Inicio > Geometría plana > Enlaces y tangencias

Delinear a escala 2:1 la pieza de ajedrez cuyo croquis acotado se adjunta. En la parábola, la distancia de la directriz, que es tangente a la esfera de la cabeza al foco F1 es 2,5 mm.

---

SOLUCIÓN

1 – Empezamos dibujando desde la parte inferior y trazamos un rectángulo de 40×3.

2 – Hacer otro rectángulo de 30×3, a 21 mm desde la línea inferior.

3 – Dibujar un tercer rectángulo de 12×3, a 50 mm desde la línea inferior.

4 – Desde la línea inferior hacer una paralela a 64 mm y donde corte al eje central dibujar una circunferencia de diámetro 15.

5 – Entre el último rectángulo y la circunferencia trazar paralelas al eje central hacia ambos lados a una distancia de 7/2 mm.

6 – Por el punto inferior de la circunferencia superior hacer una perpendicular al eje y esta es la recta directriz de la parábola. Situar su foco a 2’5 mm más abajo. Trazar la parábola, conocida la directriz y el foco, mediante el método por puntos.

7 – Determinar los puntos A y B (vértices de la hipérbola) a 13 mm de la línea inferior y a 15/2 de la línea central hacia cada lado.

8 – Situar los focos, F y F’, a 20/2 del eje central sobre la misma línea en la que está A y B.

9 – Dibujar la hipérbola por puntos conocidos los dos focos y los vértices

---

Inicio > Geometría plana > Enlaces y tangencias | | Vídeos sobre enlaces y tangencias

 

enlaces y tangencias – 2