Inicio > Geometría plana > Homología
Dado un cuadrilátero (trapezoide) y un punto V, exterior; definir una homología que transforme dicho cuadrilátero en un paralelogramo de área equivalente al cuadrilátero (siendo V el centro de homología).
SOLUCIÓN
Lo ilustraré en el siguiente ejemplo :
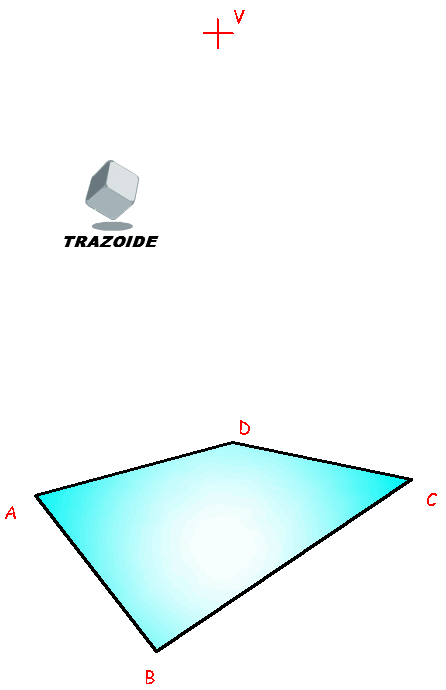
Inicialmente tenemos el cuadrilátero ABCD y el centro de homología, V.
Como deseas que se transforme en un paralelogramo, se prolongan los lados opuestos del cuadrilátero dado hasta que se corten y uniendo esos puntos de corte, X e Y, se consigue la recta límite.
Ahora el problema viene en conseguir algún dato del paralelogramo que se pide. No especifican cuál será, cuadrado, rectángulo, rombo o romboide, por lo que ahora mismo podría ser cualquiera de esos cuatro. Pero para el rectángulo, rombo y romboide se necesitaría tener algún dato de él, mientras que para el cuadrado no es necesario (porque la base y la altura son iguales), por lo tanto supondré que se solicita un cuadrado.
Para hacer un cuadrado equivalente al trapezoide dado, primero transformo el cuadrilátero en un triángulo equivalente, para ello uno dos de sus vértices, línea magenta, (lo he dibujado aparte de la homología en el siguiente dibujo, para que esté más claro, pero se puede hacer encima) y se hace una paralela por el otro vértice. Prolongando el lado contiguo se obtiene un triángulo equivalente (el que ves rayado), que tendrá de base la señalada como b y de altura la marcada con h.
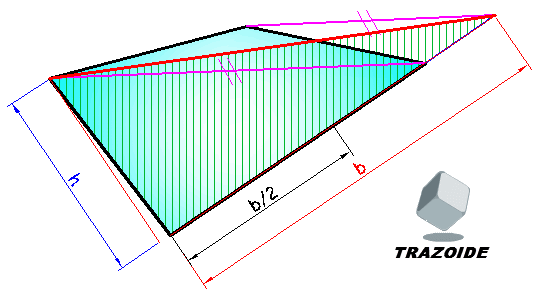
Ahora, se transforma el triángulo obtenido en un cuadrado, para ello se igualan las áreas b·h/2 = L·L, por lo tanto, se conocen dos segmentos, b/2 y h, así que, plantearé una media proporcional para obtener el valor del lado del cuadrado, L (en el siguiente dibujo). La mitad de la base, b/2, y la altura, h, me han salido muy parecidas, pero no tienen por qué ser iguales.
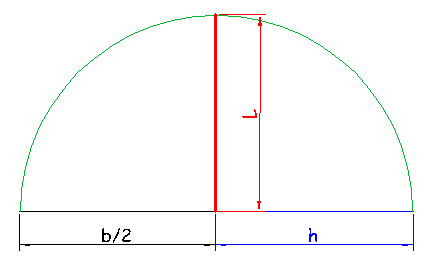
Conocido el valor del lado del cuadrado se trata de llevarlo a la homología. Se prolonga uno de los lados hasta la recta límite, por ejemplo el AB, al unirlo con el centro de homología se consigue la dirección de la recta homóloga, A’B’. Sobre ella y a partir del centro de homología se lleva el valor del lado del cuadrado, L, hallado anteriormente. Dibujando una paralela a la unión del centro de homología con el vértice B por el extremo de esa longitud, L, se obtiene el punto A’ donde corte a la unión del centro de homología con el vértice A.
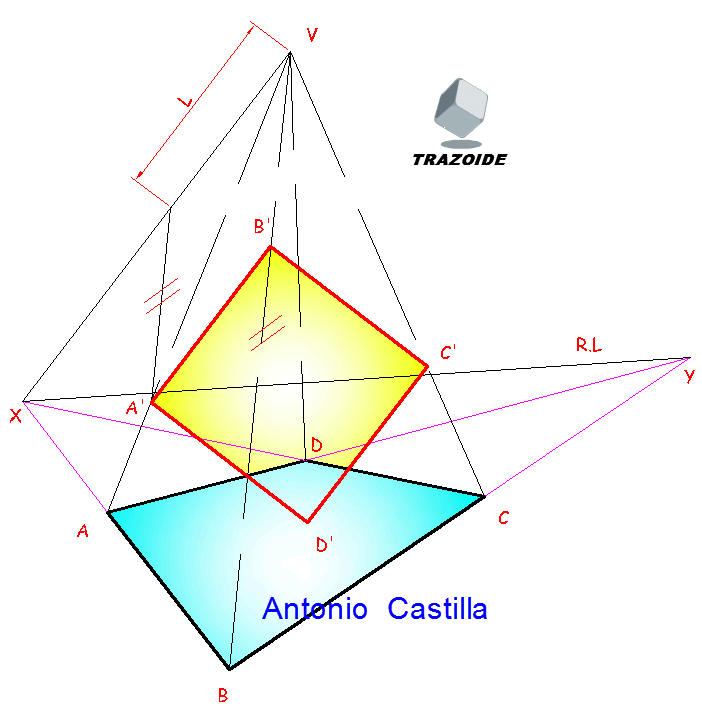
Con centro en A’ y radio el lado del cuadrado se traza un arco. Donde el arco corta a la unión de V con B es su homólogo B’. También se puede dibujar una paralela a VX por A’ y donde corte a VB es B’.
Conocido el lado del cuadrado A’B’ se dibuja este con líneas perpendiculares y llevando la longitud L.
Inicio > Geometría plana > Homología | | Vídeos sobre homología
homología – 980






Buenas tardes, estaba haciendo el ejercicio (enhorabuena por la explicación detellada) pero no me queda claro con que direccción se coloca el lado AB en la homología una vez obtenido su valor.
Un saludo y gracias de antemano =)
.
Hola Andrea.
He mejorado la calidad de las imágenes y he añadido algunos pasos más después de la última imagen. Ahí explico lo que necesitas.
Buenos días. Gracias por el trabajo que nos ayuda a avanzar en esta materia. He estado trabajando en este problema de diferentes modos.
1.- dado V y la figura fijos no he sabido resolver el problema.
2.- Dada la figura ABCD he situado el vértice V teniendo en cuenta dos datos a) que los lados A’B’ y C’D’ han de ser perpendiculares por lo que AB y CD que confluyen en un punto 1 y AC y BD que confluyen en un punto 2 de donde V ha de estar sobre una circunferencia de diámetro 1,2. Del mismo modo las diagonales del cuadrado han de ser perpendiculares ( como el punto de la diagonal
AC se salía del cuadro del dibujo lo he sustituido por saber que el lado del cuadrado con la diagonal forma 45 y he construido el arco capaz del segmento 1,3 (3 es la intersección de BD con la recta límite 1,2) con el ángulo de 45 grados. El punto de corte de la semicircunferencia 1,2 y el arco capaz me da la situación de V.
Luego he procedido como indica la resolución del problema.
¿Está bien? porque el enunciado parece decir o he creído que V y la figura son fijos y, en ese caso, no he sabido resolverlo.
Gracias por vuestro trabajo.