Inicio > Geometría plana > Enlaces y tangencias
Esta entrada es la transcripción del vídeo sobre el método para resolver tangencias mediante potencia. Puede ver el vídeo pulsando aquí.
- Esquema en blanco y negro para descargar, en PDF.
- Esquema con líneas a color para descargar, en PDF.
- Esquema completamente coloreado para descargar, en PDF.
- Esquema en blanco y negro para descargar, en PNG (botón derecho «Guardar como»).
- Esquema con líneas a color para descargar, en PNG (botón derecho «Guardar como»).
- Esquema completamente coloreado para descargar, en PNG (botón derecho «Guardar como»).
¿Sabes cuándo debes aplicar potencia para resolver una tangencia?, ¿sabes cómo aplicarla?
SOLUCIÓN
Partamos de una circunferencia y dibujemos otras dos cualesquiera que sean tangentes a la primera. Repasemos cómo se dibujaba el eje radical de dos circunferencias tangentes. Era una perpendicular a la unión de los centros por el punto de tangencia. Y el punto de corte de dos ejes radicales era el centro radical. Si medimos la distancia que hay desde el centro radical a los puntos de tangencia veremos que es la misma distancia. Luego, si tenemos una de estas distancias podemos encontrar dónde está el otro punto de tangencia.
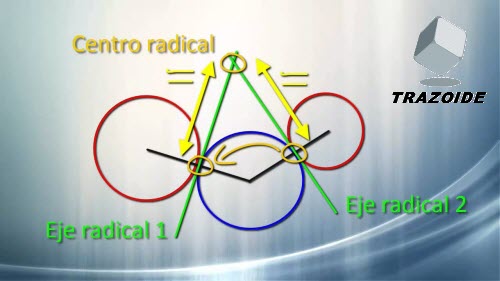
Bueno, pues todo esto es el proceso que vamos a seguir. Primero debemos buscar dos ejes radicales y con estos el centro radical. Haciendo tangentes desde el centro radical dibujaremos un arco que tendrá a todos los puntos de tangencia que buscamos. Vamos a repetir. Necesitamos hallar dos ejes radicales, después el centro radical y desde ahí las tangentes para tener los puntos de tangencia. Si podemos recordar estos tres simples pasos el resto es adaptarlo a las condiciones particulares de cada problema.

Lo que hemos explicado es el núcleo del procedimiento. Vamos a desarrollarlo cómo sería aplicando todos los casos que se nos pueden dar. Para ello te aconsejaría que cojas un papel y un bolígrafo y vayas haciendo un esquema propio, yo te ofreceré el mío, que puedes descargar pulsando en los siguientes enlaces :
- Esquema en blanco y negro para descargar.
- Esquema con líneas a color para descargar.
- Esquema completamente coloreado para descargar.
Lo primero es tener claro cuándo podemos utilizar potencia para hallar unas circunferencias tangentes, porque no siempre se puede utilizar.
Solo podemos utilizar potencia cuando se conozca la recta en la que estará el centro de la circunferencia buscada.
Esa recta nos la pueden dar en el enunciado del problema, pero también la podemos localizar con otros datos. Tenemos cuatro posibles casos.
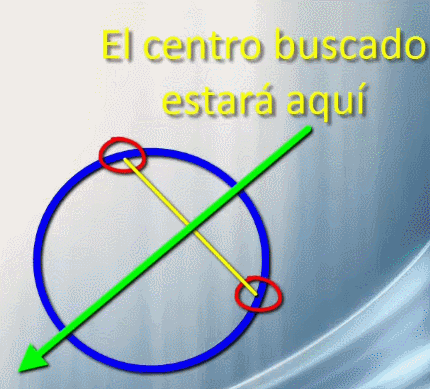
Si conoces dos puntos por los que pasará la circunferencia buscada su centro estará en la mediatriz de los dos puntos.
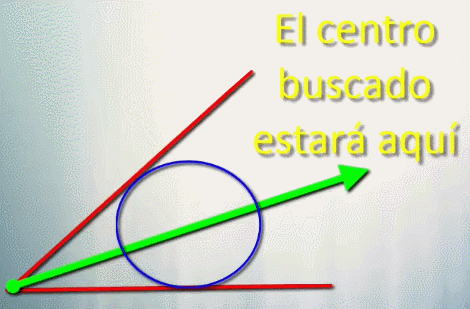
Si la respuesta es negativa nos preguntamos ¿tenemos dos rectas tangentes? En caso afirmativo los centros de las circunferencias tangentes están en la bisectriz del ángulo.
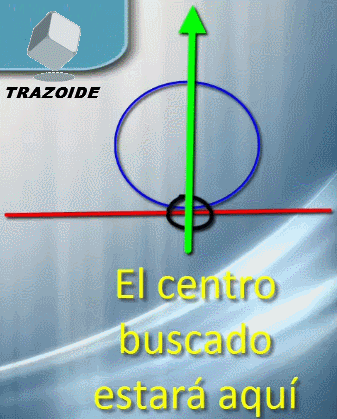
Si tampoco ese es nuestro caso, nos volvemos a preguntar ¿tenemos una recta tangente y el punto de tangencia sobre ella?, si la respuesta es sí el centro de la circunferencia que buscamos está en la perpendicular a la recta por el punto de tangencia.
Queda un caso más. ¿Tenemos una circunferencia tangente y el punto de tangencia en ella?, si es nuestro caso la recta que contiene al centro de la circunferencia buscada estará en la unión del centro de la circunferencia dada y el punto de tangencia.
Si no consiguiéramos localizar la recta que contiene el centro de la circunferencia buscada entonces debemos de aplicar otro procedimiento distinto a la potencia.
Aunque esta primera parte pueda parecer un poco larga o complicada solo hay que pararse a pensar que lo único que hemos hecho es localizar dónde estará el centro de la circunferencia buscada mediante cuatro procedimientos que ya conocemos, circunferencia que pasa por dos puntos, tangente a dos rectas, tangente a una recta por un punto y tangente a una circunferencia por un punto.

Ya tenemos el primer requisito, conocemos la recta en la que estará el centro de la circunferencia buscada.
Pero aún nos podemos encontrar con una dificultad más, y es que necesitamos tener tres elementos para hallar la tangencia. Estos elementos pueden ser puntos, rectas o circunferencias en cualquier combinación. Las circunferencias que buscamos deben ser tangentes o pasar por esos elementos, luego, no hay que contar la recta que contiene a los centros.
Si solo tenemos dos elementos determinar el tercero es sencillo, solo tenemos que hacer el simétrico de uno de ellos respecto de la recta en la que está el centro de la circunferencia buscada.

Repasemos, hasta ahora lo que hemos hecho es asegurarnos de que tenemos todo lo necesario para resolver el problema. Primero determinamos la recta que contiene al centro de la circunferencia que buscamos y después nos aseguramos de que tenemos tres elementos. Ahora es cuando empezaremos a resolver el problema.
Vamos a determinar dos ejes radicales, entre la circunferencia buscada y las dadas. Recordemos que un punto también es una circunferencia, pero de radio cero. Y que una recta también es una circunferencia pero de radio infinito. Luego, siempre tenemos varias circunferencias aunque sean de radio medible, cero o infinito.
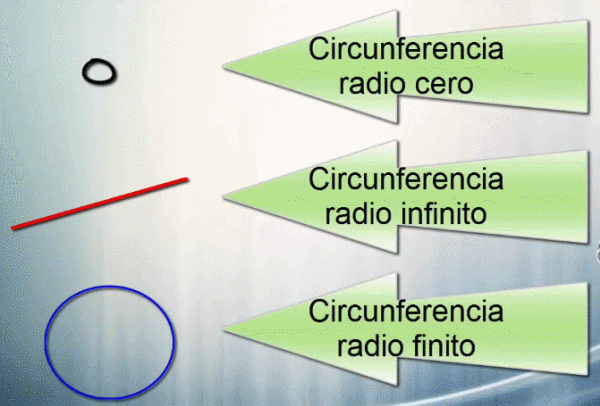
Pueden presentarse cinco casos, y que se basan en las propiedades de los ejes radicales, vamos a repasarlas.
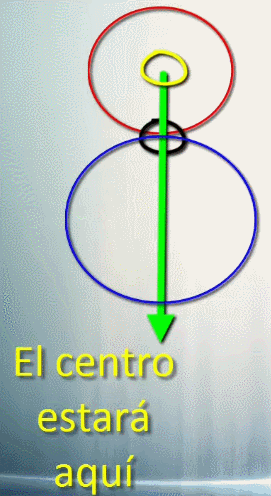
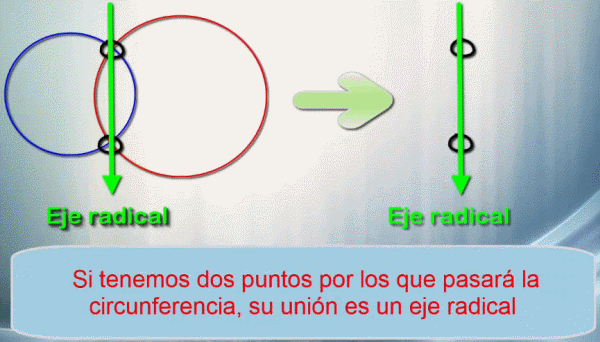
Si dos circunferencias se cortan (son secantes) el eje radical es la unión de los puntos de corte. Luego, si tenemos dos puntos por los que pasará la circunferencia la unión de esos dos puntos ya es un eje radical. Ya tenemos una forma de localizar un eje radical.
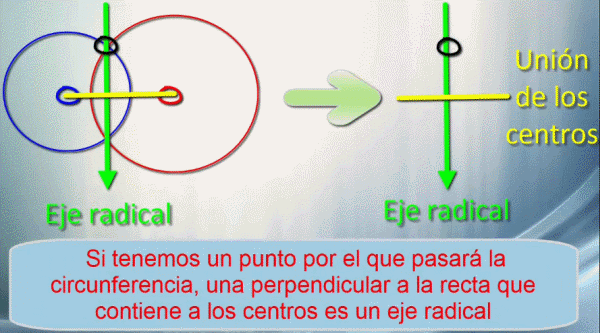
Otra propiedad nos dice que los ejes radicales son perpendiculares a la unión de los centros. Esta propiedad junto con la anterior nos permite decir que si tenemos un punto por el que pasará la circunferencia al dibujar una perpendicular a la recta que contiene al centro de la circunferencia buscada pasando por el punto tenemos otro eje radical.
Cuando dos circunferencias son tangentes su eje radical es la recta tangente por el punto de contacto. O dicho al revés, si se conoce una recta tangente esta es un eje radical.
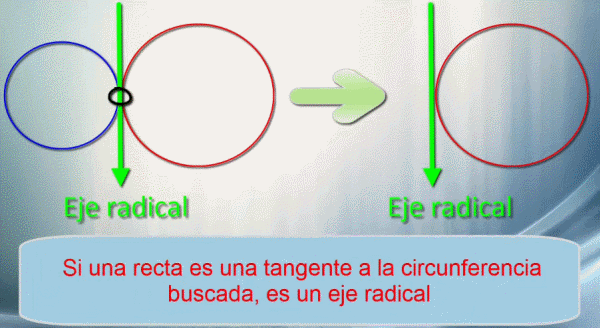
El caso más genérico es cuando tenemos dos circunferencias que no se cortan (exteriores o no secantes). Para hallar su centro radical dibujamos una circunferencia auxiliar cualquiera que corte a las dos dadas. Se unen los puntos de corte y por donde se cortan esas dos rectas pasará el eje radical en perpendicular a la unión de los centros. Luego, si tenemos dos circunferencias se puede emplear ese procedimiento o los dos anteriores para hallar su eje radical. Insistimos en que esto es aplicable aunque una de las circunferencias sea un punto (radio cero) o una recta (radio infinito).
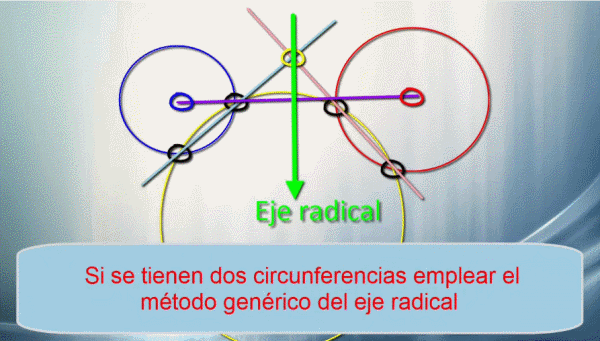
El anterior procedimiento también se puede aplicar a cualquier circunferencia que tenga su centro en la recta que contiene al centro de la buscada, que pasa por el punto dado y corta a otra circunferencia dada. Donde se corten ambas circunferencias es el eje radical.
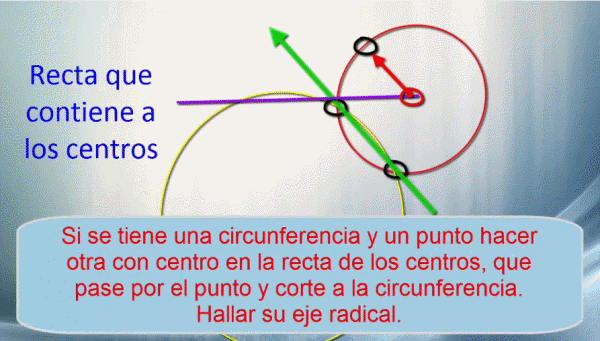
Recapitulemos, lo que debemos hacer es hallar dos ejes radicales aplicando las propiedades de estos. Y esto lo necesitábamos para determinar el centro radical. Esta es la parte más fácil pues el centro radical es el punto donde se cortan los dos ejes radicales.
El centro radical era el punto desde el que las tangentes median lo mismo. Por lo que ahora buscaremos las tangentes y esto nos dará los puntos de tangencia. Se nos pueden presentar tres casos.
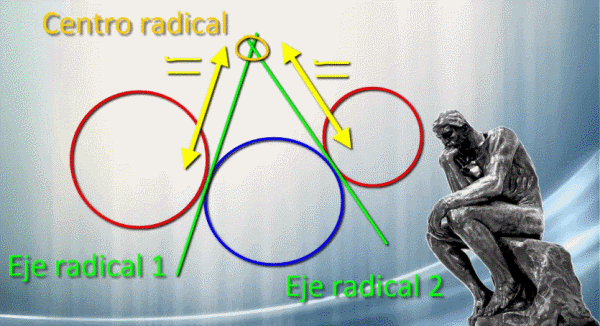
Si ya tenemos un punto de tangencia, es el caso más simple, al unir el centro radical con ese punto ya tenemos el valor de una tangente.
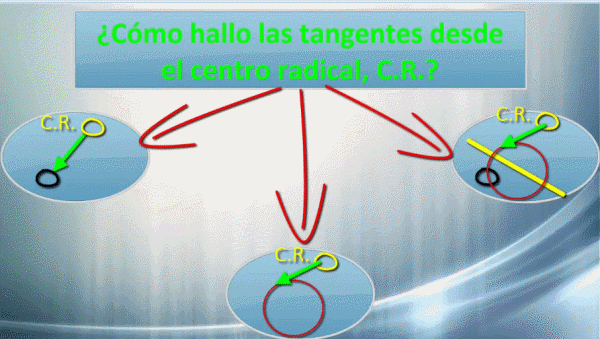
Si tenemos una circunferencia hallamos la tangente desde el centro radical a dicha circunferencia y evidentemente tenemos el valor de la tangente.
Si tenemos un punto por el que pasará la circunferencia buscada se puede buscar una circunferencia auxiliar con centro en la recta que contiene al centro de la buscada y radio hasta el punto. Y estamos en el caso anterior, trazar la tangente a la circunferencia desde el centro radical.
Como todas las tangentes deben medir lo mismo desde el centro radical las buscaremos trazando un arco con centro en el centro radical y radio la tangente hallada. Donde este arco corte a los otros elementos de la tangencia son los puntos de tangencia buscados.
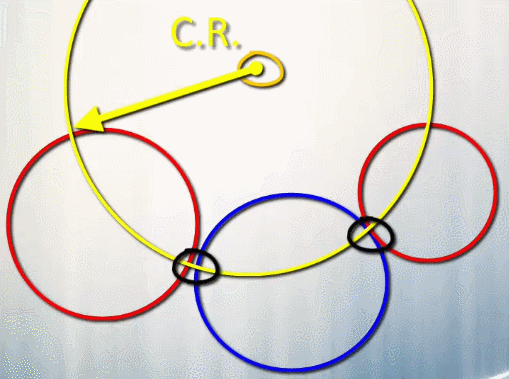
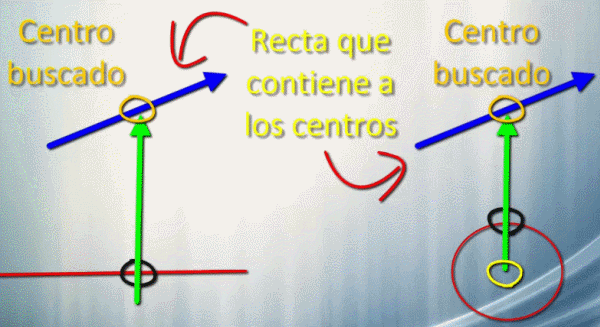
Ya está casi resuelto. Tenemos los puntos de tangencia y la recta en la que están los centros. Con los conceptos básicos de tangencia hallaremos los centros.
Si se tiene una recta dibujar una perpendicular a ella por el punto de tangencia y si se tiene una circunferencia se une el punto de tangencia en ella con su centro, donde corten a la recta que contiene a los centros es el centro de la solución.
Un último repaso. Para utilizar potencias debemos conocer la recta que contiene a los centros, hallar dos ejes radicales, el centro radical y las tangentes desde él.

En los próximos vídeos aplicaremos el procedimiento a distintos problemas para comprobar que todos se resuelven igual, visita nuestro canal de vídeos https://www.youtube.com/user/canaltrazoide/videos
Inicio > Geometría plana > Enlaces y tangencias | | Vídeos sobre enlaces y tangencias
enlaces-119





