El ovoide está formado por cuatro arcos de circunferencias y tiene un único eje de simetría, el eje mayor.
En este vídeo se explica cómo dibujar un ovoide conocidos ambos ejes, el mayor y el menor.
Volver al índice de vídeos de ENLACES Y TANGENCIAS
Estás en : Geometría plana > Enlaces y tangencias > Ovoides







Hola, buenas!
Estaba viendo este video de cómo construir un ovoide dados sus dos ejes y hay un procedimiento que hace que no lo termino de ver claro…
Entiendo cómo determina los puntos de tangencia de la circunferencia superior (siguiendo el mismo método para dibujar un ovoide sabiendo sólo su eje menor, no?). Pero si queremos que las circunferencias laterales sean tangentes tanto a la circunferencia superior como a la inferior… ya tenemos marcado el punto de circunferencia, porque si unimos punto de tangencia-centro de cada una y alargamos las rectas, llega un punto donde ambas rectas se cortan. Es por ello que no entiendo el procedimiento (sobre el minuto 3:19), porque esos centros que marca no cumplen la regla de tangencia a los dos puntos que unen.
Puede que me haya hecho un lío, pero sigo sin verlo.
Muchas gracias!
O es que simplemente no tienen que ser tangencias?
Empezando por el final, decirte que sí, los arcos deben ser tangentes siempre.
Respecto del procedimiento, tiene un fallo, como bien has detectado.
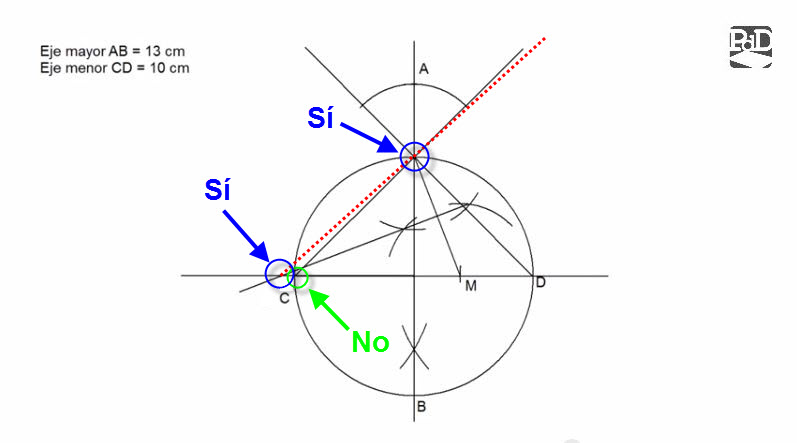
El problema es que se han calculado los puntos de tangencia antes de tener determinados todos los centros. En el minuto 1:32 indica que se debe de unir C con el punto superior de la circunferencia y eso es lo que NO se debe de hacer, al igual que con D.
El resto del procedimiento está bien, y claro, al final habría que añadirle que se deben unir los centros de los dos arcos laterales con el centro del arco superior para determinar los puntos de tangencia.
Como complemento te diré que aunque en este vídeo el centro del arco superior se toma en el punto más alto de la circunferencia, el método genérico indica que se toma a una distancia la que se desee respecto del extremo superior del eje mayor y que esa misma distancia es la que se lleva desde los extremos del eje menor.
Gracias por el aviso. Mientras se arregla, dejaré una nota en la descripción del vídeo advirtiendo ese fallo.
¡Muchas gracias!