Ejercicios de inversión – 967
Inicio > Geometría plana > Inversión
Trazar una circunferencia que pase por dos puntos, A y B, y corte en puntos diametralmente opuestos a otra circunferencia dada de centro C.
SOLUCIÓN
1 – Plantear una inversión de centro de inversión en el centro de la circunferencia, C, y potencia negativa
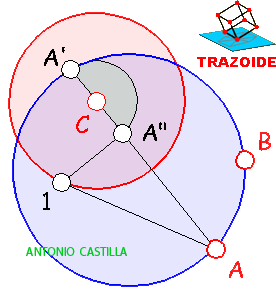
2 – Hallar el inverso, A’, de uno de los puntos, A
Para conseguir A", se ha tomado el centro C como centro de inversión y la circunferencia dada (roja) como circunferencia de autoinversión (o de puntos dobles). Ahora se halla el inverso del punto A. Para ello se ha trazado la tangente desde A a la circunferencia, obteniendo el punto de tangencia 1. Se une el punto dado A, con el centro de inversión, C, y desde el punto de tangencia, 1, se hace una perpendicular a A-C. Donde la toque, A", es el inverso (con potencia positiva) del punto A.
Para hallar su inverso, A’, con potencia negativa, solo hay que girarlo 180º alrededor del centro, C.
3 – Hacer una circunferencia que pase por la pareja de puntos inversos, A y A’, y el otro punto conocido, B, esa es la circunferencia buscada
Inicio > Geometría plana > Inversión





