Ejercicios resueltos de enlaces y tangencias – 70
Inicio > Geometría plana > Enlaces y tangencias
Dados un punto, una recta y una circunferencia, hallar las circunferencias cuyo centro se encuentra en la recta, R, son tangentes a la circunferencia, A, y pasan por el punto, P.
SOLUCIÓN
Puedes ver cómo resolver tangencias mediante potencia explicado en un vídeo pulsando aquí.
Dan la recta en la que debe estar el centro, R, y en ella estará contenido un diámetro de la circunferencia buscada.
Los diámetros dividen a las circunferencias en dos partes iguales (simétricas), luego, se tiene el eje de simetría (la recta que contiene al centro, R), por lo que si se hace el simétrico del punto dado, P, respecto de esa recta, R, se tendrá un segundo punto de la circunferencia buscada.
El problema ha quedado reducido a otro : trazar las circunferencias tangentes a la circunferencia dada y que pasen por dos puntos (el dado y su simétrico respecto de la recta que contiene a los centros).
Para resolverlo se pueden utilizar dos procedimientos, potencia o inversión.
Por potencia su solución sería así :
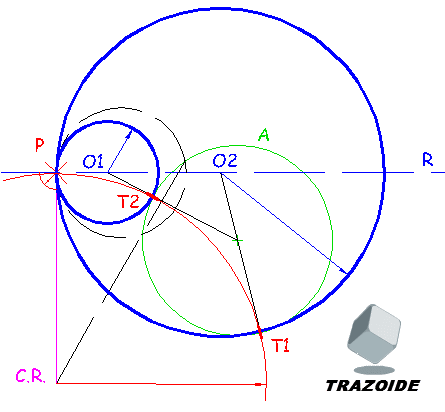
1 – Suponiendo el ejercicio resuelto (las soluciones están en línea azul gruesa). El punto P dado es de la circunferencia buscada y el centro debe estar sobre la recta R, si quisiéramos trazar una recta tangente se hará una perpendicular al radio que une el punto de tangencia deseado, P, con el centro, y esa es la recta R dada, luego, al hacerle una perpendicular a R por el punto P se ha dibujado una recta tangente a la circunferencia buscada (en magenta).
2 – Ahora recordemos una propiedad (esta es solo una hay otras) fundamental del centro radical de dos circunferencias : «el centro radical, C.R., es el punto por el que pasan las tangentes a tres circunferencias que miden lo mismo». Se puede expresar de otras formas pero así está más claro lo que quiero hacer, y es buscar el centro radical, porque ya que tengo una tangente, si localizo otra que mide lo mismo respecto de la circunferencia dada, A, tendré los puntos de tangencia de la solución buscada con la dada, A.
3 – Para determinar el centro radical se dibujan dos ejes radicales y donde estos se corten es el centro radical. Como la circunferencia dada debe tener su centro sobre la recta R, buscaré una circunferencia cualquiera con su centro en dicha recta R, que pase por P y que corte a la dada A (la que está en negro a trazos).
4 – Se determina el otro eje radical (entre la elegida al azar y la dada A), simplemente uniendo los puntos de corte de ambas (en negro a trazos). Donde se corte con la anterior es el centro radical (marcado con C.R.).
5 – Si con centro en el centro radical (C.R.) y radio hasta el punto P hago un arco (línea fina roja) que corta a la circunferencia dada en T1 y T2. Lo que he hecho ha sido localizar los puntos de tangencia de la circunferencia dada A que miden lo mismo que la tangente desde la circunferencia buscada.
También se podrían hacer las tangentes a la circunferencia dada A desde el centro radical (C.R), y se obtienen los puntos de tangencia T1 y T2 (cada uno es para una solución distinta).
6 – Los puntos obtenidos son los puntos de tangencia con la circunferencia dada, para hallar los centros de la solución, O1 y O2, basta con unirlos con el centro de la circunferencia dada.
Inicio > Geometría plana > Enlaces y tangencias | | Vídeos sobre enlaces y tangencias
enlaces-70





