Rectas dadas la distancia que las separa 970
Inicio > Sistema diédrico > Distancias en diédrico
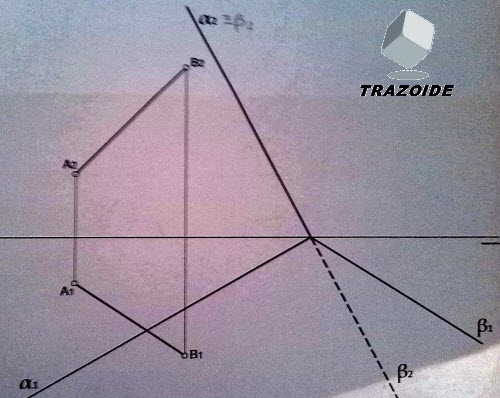
Dadas las proyecciones, verticales y horizontales, de dos puntos A y B, y de dos planos P y Q en el sistema diédrico, se pide:
a) Hallar una recta R que pasa por A y otra recta S que pase por B sabiendo que:
– El segmento AB dado es la mínima distancia (es decir, perpendicular común) entre las rectas R y S que se piden.
– La recta R es paralela al plano P y la recta S es paralela al plano Q.
b) Obtener la verdadera magnitud entre el segmento AB (indicarlo de forma gráfica y numéricamente).
c) Hallar el ángulo que forma el plano Q con el plano horizontal de proyección (indicarlo gráfica y numéricamente).
SOLUCIÓN
1 – Dibujar un plano, M, perpendicular al segmento AB, pasando por A.
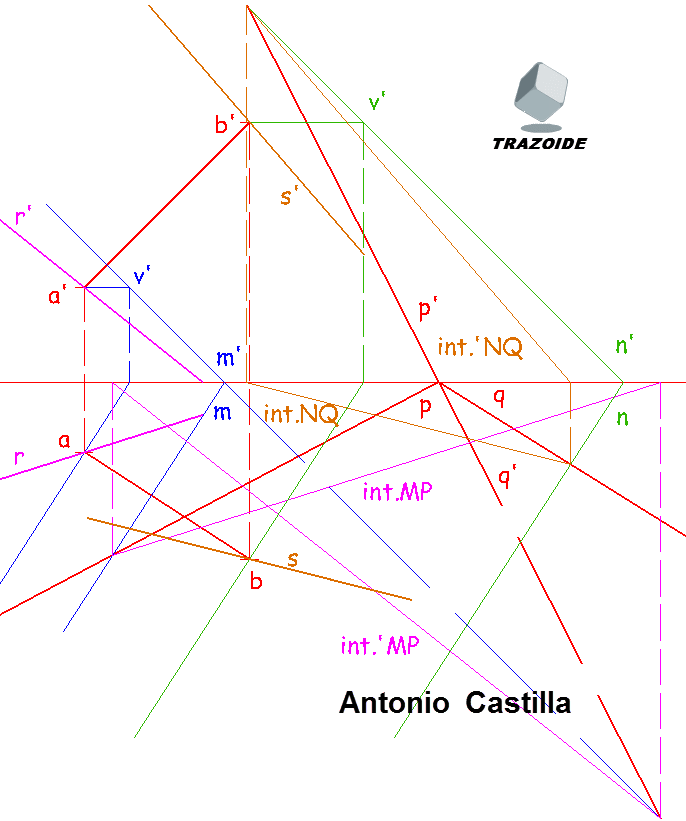
2 – Hallar la intersección entre M y P, a la que llamaré Int.MP.
3 – Trazar una paralela a Int. MP por el punto A y esta es una de las dos rectas pedidas, R.
4 – Realizaremos el mismo procedimiento con B. Dibujar un plano, N, perpendicular a AB por B.
5 – Dibujar la intersección entre N y Q (Int. NQ).
6 – Paralela a Int. NQ por B nos da la segunda recta buscada, S.
También se puede hacer de otra forma (que en esencia es lo mismo) y que puede que no necesite tanto espacio en el papel.
a – Dibujar un plano, M, perpendicular al segmento AB, pasando por A.
b – Dibujar otro plano, K, paralelo a P que pase por A.
c – Hallar la intersección entre K y M, y esta es ya una de las rectas buscadas, R.
d – Realizaremos el mismo procedimiento con B. Dibujar un plano, N, perpendicular a AB por B.
e – Dibujar otro plano, L, paralelo a Q que pase por B.
f – Hallar la intersección entre L y N, y esta es ya la segunda recta buscada, S.
Inicio > Sistema diédrico > Distancias en diédrico | | Vídeos sobre distancias





