Triángulos – 982
Inicio > Geometría plana > Triángulos
Triángulo isósceles conocida la altura, hb, y la mediana, mb, respecto de un mismo vértice B.
SOLUCIÓN
1 – Dibujar una recta (horizontal en mi dibujo) y sobre ella en cualquier punto una perpendicular con la medida de la altura, XB = hb. El extremo B es uno de los vértices del triángulo.
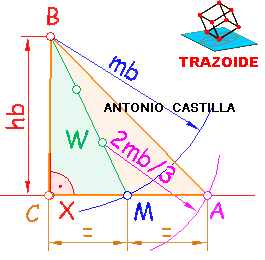
2 – Con centro en el extremo de la altura, B, y radio la mediana, mb, se traza un arco que corte a la recta inicial. Este punto, M, es el punto medio del lado b.
3 – Unir B con M y dividirlo en tres partes iguales.
4 – Tomar centro en la segunda división, W, a partir de B (baricentro) y con radio 2·mb/3 se dibuja un arco que corte a la línea inicial. El punto de corte, A, es el segundo vértice del triángulo.
5 – Sobre la recta inicial llevar la medida A-M hacia el otro lado y se consigue el tercer vértice C.
Nota : Con las medidas del problema el triángulo isósceles sale casi rectángulo, de ahí el que los puntos X y C o los segmentos XB y CB estén casi coincidentes.
Inicio > Geometría plana > Triángulos | | Vídeos sobre triángulos





